Class 12 Exam > Class 12 Questions > Two slits separated by a distance of 1mm are ...
Start Learning for Free
Two slits separated by a distance of 1mm are illuminated with red light of wavelength 6.5 *10 *(-7) m. The interference fringes are observed on a screen placed 1m from the slits. Find the distance btw the third dark Fringe and the fifth bright fringe on the same side of the central maxima!! :please solve this?
Verified Answer
Two slits separated by a distance of 1mm are illuminated with red ligh...

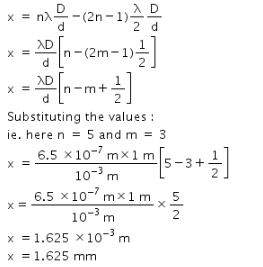
 This question is part of UPSC exam. View all Class 12 courses
This question is part of UPSC exam. View all Class 12 courses
Most Upvoted Answer
Two slits separated by a distance of 1mm are illuminated with red ligh...
Key Information:
- Distance between the two slits (d) = 1mm = 0.001m
- Wavelength of the red light (λ) = 6.5 * 10^(-7) m
- Distance between the screen and the slits (L) = 1m
Calculation:
1. Determining Fringe Spacing:
The fringe spacing, also known as the distance between two consecutive fringes, can be calculated using the formula for the double-slit interference pattern:
dsinθ = mλ
Where:
- d is the distance between the slits (0.001m)
- θ is the angle between the central maximum and the mth fringe
- m is the order of the fringe (1, 2, 3, ...)
- λ is the wavelength of light (6.5 * 10^(-7) m)
For the central maximum (m = 0), sinθ = 0, so the first bright fringe occurs when m = 1.
dsinθ = λ
θ = sin^(-1)(λ/d)
Substituting the values, we can find the angle θ:
θ = sin^(-1)(6.5 * 10^(-7) / 0.001)
θ ≈ 0.000409 radians
2. Finding the Distance between Fringes:
The distance between adjacent fringes can be determined using the formula:
y = L * tanθ
Where:
- y is the distance between fringes
- L is the distance between the screen and the slits (1m)
- θ is the angle between the central maximum and the mth fringe (0.000409 radians)
For the third dark fringe (m = 3), the distance from the central maximum can be calculated:
y = 1 * tan(3 * 0.000409)
y ≈ 0.00122m
For the fifth bright fringe (m = 5), the distance from the central maximum can be calculated:
y = 1 * tan(5 * 0.000409)
y ≈ 0.00203m
Final Result:
The distance between the third dark fringe and the fifth bright fringe on the same side of the central maximum is approximately 0.00122m.
- Distance between the two slits (d) = 1mm = 0.001m
- Wavelength of the red light (λ) = 6.5 * 10^(-7) m
- Distance between the screen and the slits (L) = 1m
Calculation:
1. Determining Fringe Spacing:
The fringe spacing, also known as the distance between two consecutive fringes, can be calculated using the formula for the double-slit interference pattern:
dsinθ = mλ
Where:
- d is the distance between the slits (0.001m)
- θ is the angle between the central maximum and the mth fringe
- m is the order of the fringe (1, 2, 3, ...)
- λ is the wavelength of light (6.5 * 10^(-7) m)
For the central maximum (m = 0), sinθ = 0, so the first bright fringe occurs when m = 1.
dsinθ = λ
θ = sin^(-1)(λ/d)
Substituting the values, we can find the angle θ:
θ = sin^(-1)(6.5 * 10^(-7) / 0.001)
θ ≈ 0.000409 radians
2. Finding the Distance between Fringes:
The distance between adjacent fringes can be determined using the formula:
y = L * tanθ
Where:
- y is the distance between fringes
- L is the distance between the screen and the slits (1m)
- θ is the angle between the central maximum and the mth fringe (0.000409 radians)
For the third dark fringe (m = 3), the distance from the central maximum can be calculated:
y = 1 * tan(3 * 0.000409)
y ≈ 0.00122m
For the fifth bright fringe (m = 5), the distance from the central maximum can be calculated:
y = 1 * tan(5 * 0.000409)
y ≈ 0.00203m
Final Result:
The distance between the third dark fringe and the fifth bright fringe on the same side of the central maximum is approximately 0.00122m.

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
Two slits separated by a distance of 1mm are illuminated with red light of wavelength 6.5 *10 *(-7) m. The interference fringes are observed on a screen placed 1m from the slits. Find the distance btw the third dark Fringe and the fifth bright fringe on the same side of the central maxima!! :please solve this?
Question Description
Two slits separated by a distance of 1mm are illuminated with red light of wavelength 6.5 *10 *(-7) m. The interference fringes are observed on a screen placed 1m from the slits. Find the distance btw the third dark Fringe and the fifth bright fringe on the same side of the central maxima!! :please solve this? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Two slits separated by a distance of 1mm are illuminated with red light of wavelength 6.5 *10 *(-7) m. The interference fringes are observed on a screen placed 1m from the slits. Find the distance btw the third dark Fringe and the fifth bright fringe on the same side of the central maxima!! :please solve this? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two slits separated by a distance of 1mm are illuminated with red light of wavelength 6.5 *10 *(-7) m. The interference fringes are observed on a screen placed 1m from the slits. Find the distance btw the third dark Fringe and the fifth bright fringe on the same side of the central maxima!! :please solve this?.
Two slits separated by a distance of 1mm are illuminated with red light of wavelength 6.5 *10 *(-7) m. The interference fringes are observed on a screen placed 1m from the slits. Find the distance btw the third dark Fringe and the fifth bright fringe on the same side of the central maxima!! :please solve this? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Two slits separated by a distance of 1mm are illuminated with red light of wavelength 6.5 *10 *(-7) m. The interference fringes are observed on a screen placed 1m from the slits. Find the distance btw the third dark Fringe and the fifth bright fringe on the same side of the central maxima!! :please solve this? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two slits separated by a distance of 1mm are illuminated with red light of wavelength 6.5 *10 *(-7) m. The interference fringes are observed on a screen placed 1m from the slits. Find the distance btw the third dark Fringe and the fifth bright fringe on the same side of the central maxima!! :please solve this?.
Solutions for Two slits separated by a distance of 1mm are illuminated with red light of wavelength 6.5 *10 *(-7) m. The interference fringes are observed on a screen placed 1m from the slits. Find the distance btw the third dark Fringe and the fifth bright fringe on the same side of the central maxima!! :please solve this? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of Two slits separated by a distance of 1mm are illuminated with red light of wavelength 6.5 *10 *(-7) m. The interference fringes are observed on a screen placed 1m from the slits. Find the distance btw the third dark Fringe and the fifth bright fringe on the same side of the central maxima!! :please solve this? defined & explained in the simplest way possible. Besides giving the explanation of
Two slits separated by a distance of 1mm are illuminated with red light of wavelength 6.5 *10 *(-7) m. The interference fringes are observed on a screen placed 1m from the slits. Find the distance btw the third dark Fringe and the fifth bright fringe on the same side of the central maxima!! :please solve this?, a detailed solution for Two slits separated by a distance of 1mm are illuminated with red light of wavelength 6.5 *10 *(-7) m. The interference fringes are observed on a screen placed 1m from the slits. Find the distance btw the third dark Fringe and the fifth bright fringe on the same side of the central maxima!! :please solve this? has been provided alongside types of Two slits separated by a distance of 1mm are illuminated with red light of wavelength 6.5 *10 *(-7) m. The interference fringes are observed on a screen placed 1m from the slits. Find the distance btw the third dark Fringe and the fifth bright fringe on the same side of the central maxima!! :please solve this? theory, EduRev gives you an
ample number of questions to practice Two slits separated by a distance of 1mm are illuminated with red light of wavelength 6.5 *10 *(-7) m. The interference fringes are observed on a screen placed 1m from the slits. Find the distance btw the third dark Fringe and the fifth bright fringe on the same side of the central maxima!! :please solve this? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















