IIT JAM Exam > IIT JAM Questions > Two spheres A and B of masses m1 and m2 respe...
Start Learning for Free
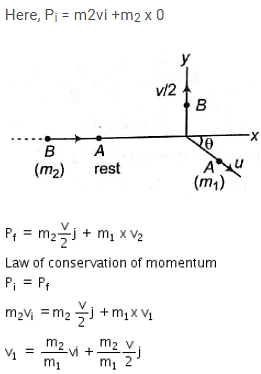
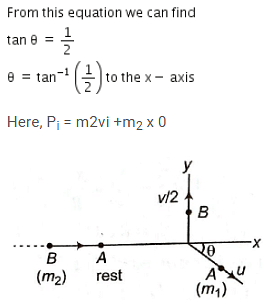
Two spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction.
Verified Answer
Two spheres A and B of masses m1 and m2 respectively collide. A is at ...

 This question is part of UPSC exam. View all IIT JAM courses
This question is part of UPSC exam. View all IIT JAM courses
Most Upvoted Answer
Two spheres A and B of masses m1 and m2 respectively collide. A is at ...
Collision between Spheres A and B
Initial Conditions:
- Sphere A is at rest initially.
- Sphere B is moving with velocity v along the x-axis.
Collision Process:
- The collision between the two spheres can be considered as a two-dimensional collision.
- The collision is assumed to be perfectly elastic, meaning there is no loss of kinetic energy during the collision.
- The spheres can be assumed to be rigid bodies.
Momentum Conservation:
- In the absence of external forces, the total momentum of the system is conserved.
- Before the collision, the momentum of Sphere B is given by:
- P₁ = m₂ * v (initial momentum)
- After the collision, Sphere B changes its direction and has a velocity of v/2 perpendicular to the original direction.
- The change in momentum of Sphere B is given by:
- ΔP = m₂ * (v/2) - m₂ * v = -m₂ * (3v/2)
- The negative sign indicates a change in direction.
- According to the principle of momentum conservation, the total momentum before the collision must be equal to the total momentum after the collision.
- Since Sphere A is initially at rest, its momentum before and after the collision is zero.
- Therefore, the change in momentum of Sphere B must be equal to the momentum of Sphere A after the collision.
- The momentum of Sphere A after the collision is given by:
- P₂ = ΔP = -m₂ * (3v/2)
Motion of Sphere A after Collision:
- The momentum of Sphere A after the collision is in the direction opposite to the initial motion of Sphere B.
- Therefore, Sphere A moves in the direction opposite to the initial motion of Sphere B.
- The magnitude of its velocity can be determined by dividing the momentum by the mass of Sphere A:
- v₂ = P₂ / m₁ = -m₂ * (3v/2) / m₁
Conclusion:
- After the collision between the spheres A and B, Sphere A moves in the direction opposite to the initial motion of Sphere B.
- The magnitude of its velocity is given by v₂ = -m₂ * (3v/2) / m₁.
Initial Conditions:
- Sphere A is at rest initially.
- Sphere B is moving with velocity v along the x-axis.
Collision Process:
- The collision between the two spheres can be considered as a two-dimensional collision.
- The collision is assumed to be perfectly elastic, meaning there is no loss of kinetic energy during the collision.
- The spheres can be assumed to be rigid bodies.
Momentum Conservation:
- In the absence of external forces, the total momentum of the system is conserved.
- Before the collision, the momentum of Sphere B is given by:
- P₁ = m₂ * v (initial momentum)
- After the collision, Sphere B changes its direction and has a velocity of v/2 perpendicular to the original direction.
- The change in momentum of Sphere B is given by:
- ΔP = m₂ * (v/2) - m₂ * v = -m₂ * (3v/2)
- The negative sign indicates a change in direction.
- According to the principle of momentum conservation, the total momentum before the collision must be equal to the total momentum after the collision.
- Since Sphere A is initially at rest, its momentum before and after the collision is zero.
- Therefore, the change in momentum of Sphere B must be equal to the momentum of Sphere A after the collision.
- The momentum of Sphere A after the collision is given by:
- P₂ = ΔP = -m₂ * (3v/2)
Motion of Sphere A after Collision:
- The momentum of Sphere A after the collision is in the direction opposite to the initial motion of Sphere B.
- Therefore, Sphere A moves in the direction opposite to the initial motion of Sphere B.
- The magnitude of its velocity can be determined by dividing the momentum by the mass of Sphere A:
- v₂ = P₂ / m₁ = -m₂ * (3v/2) / m₁
Conclusion:
- After the collision between the spheres A and B, Sphere A moves in the direction opposite to the initial motion of Sphere B.
- The magnitude of its velocity is given by v₂ = -m₂ * (3v/2) / m₁.

|
Explore Courses for IIT JAM exam
|

|
Similar IIT JAM Doubts
Two spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction.
Question Description
Two spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction. for IIT JAM 2024 is part of IIT JAM preparation. The Question and answers have been prepared according to the IIT JAM exam syllabus. Information about Two spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction. covers all topics & solutions for IIT JAM 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction..
Two spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction. for IIT JAM 2024 is part of IIT JAM preparation. The Question and answers have been prepared according to the IIT JAM exam syllabus. Information about Two spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction. covers all topics & solutions for IIT JAM 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction..
Solutions for Two spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction. in English & in Hindi are available as part of our courses for IIT JAM.
Download more important topics, notes, lectures and mock test series for IIT JAM Exam by signing up for free.
Here you can find the meaning of Two spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction. defined & explained in the simplest way possible. Besides giving the explanation of
Two spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction., a detailed solution for Two spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction. has been provided alongside types of Two spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction. theory, EduRev gives you an
ample number of questions to practice Two spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction. tests, examples and also practice IIT JAM tests.

|
Explore Courses for IIT JAM exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















