Class 11 Exam > Class 11 Questions > if it is cubic equation Related: Binomial Th...
Start Learning for Free
if it is cubic equation
Verified Answer
if it is cubic equation Related: Binomial Theorem for Positive Integr...
This article is about cubic equations in one variable. For cubic equations in two variables, see cubic plane curve.
In algebra, a cubic function is a function of the form
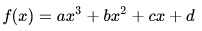
in which a is nonzero.
Setting f(x) = 0 produces a cubic equation of the form
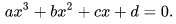
The solutions of this equation are called roots of the polynomial f(x). If all of the coefficients a, b, c, and d of the cubic equation are real numbers, then it has at least one real root (this is true for all odd degree polynomials). All of the roots of the cubic equation can be found algebraically. (This is also true of quadratic (second degree) or quartic (fourth degree) equations, but not of higher-degree equations, by the Abel–Ruffini theorem.) The roots can also be found trigonometrically. Alternatively, numerical approximations of the roots can be found using root-finding algorithms such as Newton's method.
The coefficients do not need to be complex numbers. Much of what is covered below is valid for coefficients of any field with characteristic 0 or greater than 3. The solutions of the cubic equation do not necessarily belong to the same field as the coefficients. For example, some cubic equations with rational coefficients have roots that are non-rational (and even non-real) complex numbers.
 This question is part of UPSC exam. View all Class 11 courses
This question is part of UPSC exam. View all Class 11 courses
Most Upvoted Answer
if it is cubic equation Related: Binomial Theorem for Positive Integr...
Binomial Theorem for Positive Integral Indices - Binomial Theorem, Class 11, Mathematics
The binomial theorem is a powerful tool in mathematics that allows us to expand the powers of a binomial expression. It states that for any positive integer n,
(a + b)^n = C(n, 0) * a^n * b^0 + C(n, 1) * a^(n-1) * b^1 + C(n, 2) * a^(n-2) * b^2 + ... + C(n, n-1) * a^1 * b^(n-1) + C(n, n) * a^0 * b^n
where C(n, r) represents the binomial coefficient, which is given by the formula:
C(n, r) = n! / (r! * (n-r)!)
Now, let's see how this binomial theorem can be applied to a cubic equation.
Expanding a Cubic Expression
Suppose we have a cubic expression (a + b)^3. Using the binomial theorem, we can expand this as:
(a + b)^3 = C(3, 0) * a^3 * b^0 + C(3, 1) * a^2 * b^1 + C(3, 2) * a^1 * b^2 + C(3, 3) * a^0 * b^3
Expanding each term, we get:
(a + b)^3 = 1 * a^3 * 1 + 3 * a^2 * b^1 + 3 * a^1 * b^2 + 1 * b^3
Simplifying further:
(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3
This is the expanded form of a cubic expression using the binomial theorem. It allows us to easily find the coefficients of each term without having to multiply out each term individually.
Applications of the Binomial Theorem for Cubic Equations
1. Simplifying expressions: The binomial theorem can be used to simplify complicated cubic expressions by expanding them using the binomial coefficients.
2. Finding coefficients: The binomial theorem helps in determining the coefficients of each term in the expansion of a cubic equation without the need for manual calculations.
3. Calculating probabilities: The binomial theorem is also used in probability theory to calculate the probabilities of different outcomes in experiments involving binomial distributions.
4. Series expansions: The binomial theorem is the foundation for many series expansions in mathematics, such as the Taylor series and the Maclaurin series.
In conclusion, the binomial theorem provides a powerful tool for expanding and simplifying cubic equations. It allows us to find the coefficients of each term easily and has various applications in mathematics and probability theory.
Attention Class 11 Students!
To make sure you are not studying endlessly, EduRev has designed Class 11 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 11.

|
Explore Courses for Class 11 exam
|

|
Similar Class 11 Doubts
if it is cubic equation Related: Binomial Theorem for Positive Integral Indices - Binomial Theorem, Class 11, Mathematics
Question Description
if it is cubic equation Related: Binomial Theorem for Positive Integral Indices - Binomial Theorem, Class 11, Mathematics for Class 11 2024 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about if it is cubic equation Related: Binomial Theorem for Positive Integral Indices - Binomial Theorem, Class 11, Mathematics covers all topics & solutions for Class 11 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for if it is cubic equation Related: Binomial Theorem for Positive Integral Indices - Binomial Theorem, Class 11, Mathematics.
if it is cubic equation Related: Binomial Theorem for Positive Integral Indices - Binomial Theorem, Class 11, Mathematics for Class 11 2024 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about if it is cubic equation Related: Binomial Theorem for Positive Integral Indices - Binomial Theorem, Class 11, Mathematics covers all topics & solutions for Class 11 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for if it is cubic equation Related: Binomial Theorem for Positive Integral Indices - Binomial Theorem, Class 11, Mathematics.
Solutions for if it is cubic equation Related: Binomial Theorem for Positive Integral Indices - Binomial Theorem, Class 11, Mathematics in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of if it is cubic equation Related: Binomial Theorem for Positive Integral Indices - Binomial Theorem, Class 11, Mathematics defined & explained in the simplest way possible. Besides giving the explanation of
if it is cubic equation Related: Binomial Theorem for Positive Integral Indices - Binomial Theorem, Class 11, Mathematics, a detailed solution for if it is cubic equation Related: Binomial Theorem for Positive Integral Indices - Binomial Theorem, Class 11, Mathematics has been provided alongside types of if it is cubic equation Related: Binomial Theorem for Positive Integral Indices - Binomial Theorem, Class 11, Mathematics theory, EduRev gives you an
ample number of questions to practice if it is cubic equation Related: Binomial Theorem for Positive Integral Indices - Binomial Theorem, Class 11, Mathematics tests, examples and also practice Class 11 tests.

|
Explore Courses for Class 11 exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























