Class 12 Exam > Class 12 Questions > Derive the equation of the transverse wave on...
Start Learning for Free
Derive the equation of the transverse wave on a stretched string?
Verified Answer
Derive the equation of the transverse wave on a stretched string?
Hence the velocity of a transverse wave along a stretched string is directly proportional to the square root of tension in the string and inversely proportional to the square root of linear density.
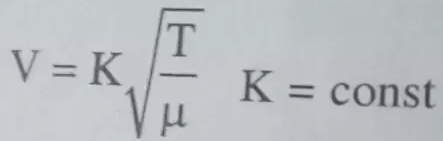
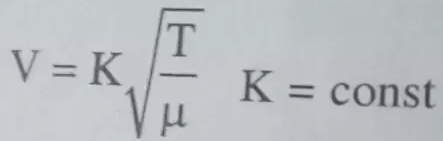
 This question is part of UPSC exam. View all Class 12 courses
This question is part of UPSC exam. View all Class 12 courses
Most Upvoted Answer
Derive the equation of the transverse wave on a stretched string?
Deriving the Equation of a Transverse Wave on a Stretched String
To derive the equation of a transverse wave on a stretched string, we need to consider the properties and characteristics of waves. A transverse wave is a type of wave where the particles of the medium vibrate perpendicular to the direction of wave propagation. In the case of a stretched string, the wave is propagated by the transverse displacement of the string.
Key Concepts:
1. Transverse wave: A wave in which the particles of the medium oscillate perpendicular to the direction of wave propagation.
2. Wave equation: An equation that describes the motion of a wave.
3. Stretched string: A string under tension that is used to transmit a wave.
Wave Equation:
The wave equation describes the motion of a wave in terms of its amplitude, wavelength, frequency, and wave speed. For a transverse wave on a stretched string, the equation can be derived as follows:
1. Consider the Displacement Function:
Let's assume that the transverse displacement of the string is given by the function y(x, t), where x is the position along the string and t is the time.
2. Derive the Equation for the Velocity:
The velocity of a point on the string is given by the derivative of the displacement function with respect to time: v = ∂y/∂t.
3. Derive the Equation for the Acceleration:
The acceleration of a point on the string is given by the derivative of the velocity with respect to time: a = ∂²y/∂t².
4. Apply Newton's Second Law:
According to Newton's second law, the force acting on a point on the string is equal to the mass of that point multiplied by its acceleration: F = μa, where μ is the linear mass density of the string.
5. Consider the Tension in the String:
The force acting on a point on the string is also equal to the tension in the string multiplied by the slope of the string at that point: F = T(∂y/∂x), where T is the tension in the string.
6. Equate the Forces:
By equating the forces in step 4 and step 5, we have T(∂y/∂x) = μ(∂²y/∂t²).
7. Solve for the Wave Equation:
Rearranging the equation, we get (∂²y/∂t²) - (T/μ)(∂²y/∂x²) = 0.
This equation is known as the wave equation for a transverse wave on a stretched string. It relates the second derivative of the displacement function with respect to time to the second derivative of the displacement function with respect to position.
Conclusion:
In conclusion, the equation of a transverse wave on a stretched string can be derived by considering the displacement function, deriving the equations for velocity and acceleration, applying Newton's second law, and equating the forces. The resulting wave equation relates the second derivatives of the displacement function with respect to time and position.
To derive the equation of a transverse wave on a stretched string, we need to consider the properties and characteristics of waves. A transverse wave is a type of wave where the particles of the medium vibrate perpendicular to the direction of wave propagation. In the case of a stretched string, the wave is propagated by the transverse displacement of the string.
Key Concepts:
1. Transverse wave: A wave in which the particles of the medium oscillate perpendicular to the direction of wave propagation.
2. Wave equation: An equation that describes the motion of a wave.
3. Stretched string: A string under tension that is used to transmit a wave.
Wave Equation:
The wave equation describes the motion of a wave in terms of its amplitude, wavelength, frequency, and wave speed. For a transverse wave on a stretched string, the equation can be derived as follows:
1. Consider the Displacement Function:
Let's assume that the transverse displacement of the string is given by the function y(x, t), where x is the position along the string and t is the time.
2. Derive the Equation for the Velocity:
The velocity of a point on the string is given by the derivative of the displacement function with respect to time: v = ∂y/∂t.
3. Derive the Equation for the Acceleration:
The acceleration of a point on the string is given by the derivative of the velocity with respect to time: a = ∂²y/∂t².
4. Apply Newton's Second Law:
According to Newton's second law, the force acting on a point on the string is equal to the mass of that point multiplied by its acceleration: F = μa, where μ is the linear mass density of the string.
5. Consider the Tension in the String:
The force acting on a point on the string is also equal to the tension in the string multiplied by the slope of the string at that point: F = T(∂y/∂x), where T is the tension in the string.
6. Equate the Forces:
By equating the forces in step 4 and step 5, we have T(∂y/∂x) = μ(∂²y/∂t²).
7. Solve for the Wave Equation:
Rearranging the equation, we get (∂²y/∂t²) - (T/μ)(∂²y/∂x²) = 0.
This equation is known as the wave equation for a transverse wave on a stretched string. It relates the second derivative of the displacement function with respect to time to the second derivative of the displacement function with respect to position.
Conclusion:
In conclusion, the equation of a transverse wave on a stretched string can be derived by considering the displacement function, deriving the equations for velocity and acceleration, applying Newton's second law, and equating the forces. The resulting wave equation relates the second derivatives of the displacement function with respect to time and position.

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
Derive the equation of the transverse wave on a stretched string?
Question Description
Derive the equation of the transverse wave on a stretched string? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Derive the equation of the transverse wave on a stretched string? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Derive the equation of the transverse wave on a stretched string?.
Derive the equation of the transverse wave on a stretched string? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Derive the equation of the transverse wave on a stretched string? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Derive the equation of the transverse wave on a stretched string?.
Solutions for Derive the equation of the transverse wave on a stretched string? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of Derive the equation of the transverse wave on a stretched string? defined & explained in the simplest way possible. Besides giving the explanation of
Derive the equation of the transverse wave on a stretched string?, a detailed solution for Derive the equation of the transverse wave on a stretched string? has been provided alongside types of Derive the equation of the transverse wave on a stretched string? theory, EduRev gives you an
ample number of questions to practice Derive the equation of the transverse wave on a stretched string? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















