Class 9 Exam > Class 9 Questions > If the density of two planets is the same,but...
Start Learning for Free
If the density of two planets is the same,but their radii are in the ratio 1:2 ,prove that the ratio of acceleration due to gravity on their surface is also 1:2.?
Verified Answer
If the density of two planets is the same,but their radii are in the r...
Ans.

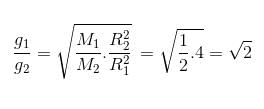

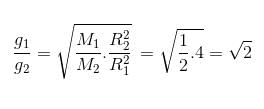
So, 1:2 Answer
 This question is part of UPSC exam. View all Class 9 courses
This question is part of UPSC exam. View all Class 9 courses
Most Upvoted Answer
If the density of two planets is the same,but their radii are in the r...
The relationship between density, radius, and acceleration due to gravity on the surface of planets:
The density, radius, and acceleration due to gravity are interconnected properties of a planet. In order to understand the relationship between them, let's break down the problem into smaller parts:
1. Density:
Density is defined as the mass of an object divided by its volume. In the case of planets, we can consider the average density, which is the total mass of the planet divided by its total volume. Mathematically, it can be expressed as:
Density = Mass / Volume
2. Volume:
The volume of a planet can be calculated using the formula for the volume of a sphere, which is given by:
Volume = (4/3) * π * (radius)^3
3. Mass:
The mass of a planet can be calculated using the formula:
Mass = Density * Volume
4. Acceleration due to gravity:
The acceleration due to gravity on the surface of a planet is given by Newton's law of universal gravitation:
Acceleration due to gravity = (G * Mass) / (radius)^2
Where G is the gravitational constant.
Proving the ratio of acceleration due to gravity:
Let's consider two planets with the same density but radii in the ratio of 1:2. We can denote the radii as r1 and r2, where r2 = 2r1.
1. Density:
Since the density is the same for both planets, we can denote it as ρ1 = ρ2 = ρ.
2. Volume:
Using the volume formula, we can calculate the volumes of the two planets as:
Volume1 = (4/3) * π * (r1)^3
Volume2 = (4/3) * π * (r2)^3 = (4/3) * π * (2r1)^3 = (4/3) * π * 8 * (r1)^3 = 8 * (4/3) * π * (r1)^3 = 8 * Volume1
3. Mass:
Since the density is the same for both planets, the masses can be calculated as:
Mass1 = ρ * Volume1
Mass2 = ρ * Volume2 = ρ * 8 * Volume1 = 8 * Mass1
4. Acceleration due to gravity:
Using Newton's law of universal gravitation, we can calculate the acceleration due to gravity for the two planets as:
Acceleration due to gravity1 = (G * Mass1) / (r1)^2
Acceleration due to gravity2 = (G * Mass2) / (r2)^2 = (G * 8 * Mass1) / (2r1)^2 = (G * 8 * Mass1) / 4 * (r1)^2 = 2 * (G * Mass1) / (r1)^2 = 2 * Acceleration due to gravity1
Conclusion:
From the calculations above, we can see that the ratio of the acceleration due to gravity on the surface of the two planets is 1:2. This means that the planet with the larger radius has twice the acceleration due to gravity
The density, radius, and acceleration due to gravity are interconnected properties of a planet. In order to understand the relationship between them, let's break down the problem into smaller parts:
1. Density:
Density is defined as the mass of an object divided by its volume. In the case of planets, we can consider the average density, which is the total mass of the planet divided by its total volume. Mathematically, it can be expressed as:
Density = Mass / Volume
2. Volume:
The volume of a planet can be calculated using the formula for the volume of a sphere, which is given by:
Volume = (4/3) * π * (radius)^3
3. Mass:
The mass of a planet can be calculated using the formula:
Mass = Density * Volume
4. Acceleration due to gravity:
The acceleration due to gravity on the surface of a planet is given by Newton's law of universal gravitation:
Acceleration due to gravity = (G * Mass) / (radius)^2
Where G is the gravitational constant.
Proving the ratio of acceleration due to gravity:
Let's consider two planets with the same density but radii in the ratio of 1:2. We can denote the radii as r1 and r2, where r2 = 2r1.
1. Density:
Since the density is the same for both planets, we can denote it as ρ1 = ρ2 = ρ.
2. Volume:
Using the volume formula, we can calculate the volumes of the two planets as:
Volume1 = (4/3) * π * (r1)^3
Volume2 = (4/3) * π * (r2)^3 = (4/3) * π * (2r1)^3 = (4/3) * π * 8 * (r1)^3 = 8 * (4/3) * π * (r1)^3 = 8 * Volume1
3. Mass:
Since the density is the same for both planets, the masses can be calculated as:
Mass1 = ρ * Volume1
Mass2 = ρ * Volume2 = ρ * 8 * Volume1 = 8 * Mass1
4. Acceleration due to gravity:
Using Newton's law of universal gravitation, we can calculate the acceleration due to gravity for the two planets as:
Acceleration due to gravity1 = (G * Mass1) / (r1)^2
Acceleration due to gravity2 = (G * Mass2) / (r2)^2 = (G * 8 * Mass1) / (2r1)^2 = (G * 8 * Mass1) / 4 * (r1)^2 = 2 * (G * Mass1) / (r1)^2 = 2 * Acceleration due to gravity1
Conclusion:
From the calculations above, we can see that the ratio of the acceleration due to gravity on the surface of the two planets is 1:2. This means that the planet with the larger radius has twice the acceleration due to gravity
Community Answer
If the density of two planets is the same,but their radii are in the r...
Acc to law of gravitation : mg1=GM1m/R1^2
g1= GM1 / R1^2
( considering that for the first planet variables are placed with 1 and for the second with 2 )
Similarly g2 = G M2/R2^2
As we know that M2 is twice of M1 and R2 is twice of R1
So g2= G2M1/(2R1)^2
g1/g2 = G M1/R1^2 X 4R1^2/G2M1
g1:g2 = 4:2 = 2:1

|
Explore Courses for Class 9 exam
|

|
Question Description
If the density of two planets is the same,but their radii are in the ratio 1:2 ,prove that the ratio of acceleration due to gravity on their surface is also 1:2.? for Class 9 2025 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about If the density of two planets is the same,but their radii are in the ratio 1:2 ,prove that the ratio of acceleration due to gravity on their surface is also 1:2.? covers all topics & solutions for Class 9 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If the density of two planets is the same,but their radii are in the ratio 1:2 ,prove that the ratio of acceleration due to gravity on their surface is also 1:2.?.
If the density of two planets is the same,but their radii are in the ratio 1:2 ,prove that the ratio of acceleration due to gravity on their surface is also 1:2.? for Class 9 2025 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about If the density of two planets is the same,but their radii are in the ratio 1:2 ,prove that the ratio of acceleration due to gravity on their surface is also 1:2.? covers all topics & solutions for Class 9 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If the density of two planets is the same,but their radii are in the ratio 1:2 ,prove that the ratio of acceleration due to gravity on their surface is also 1:2.?.
Solutions for If the density of two planets is the same,but their radii are in the ratio 1:2 ,prove that the ratio of acceleration due to gravity on their surface is also 1:2.? in English & in Hindi are available as part of our courses for Class 9.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Here you can find the meaning of If the density of two planets is the same,but their radii are in the ratio 1:2 ,prove that the ratio of acceleration due to gravity on their surface is also 1:2.? defined & explained in the simplest way possible. Besides giving the explanation of
If the density of two planets is the same,but their radii are in the ratio 1:2 ,prove that the ratio of acceleration due to gravity on their surface is also 1:2.?, a detailed solution for If the density of two planets is the same,but their radii are in the ratio 1:2 ,prove that the ratio of acceleration due to gravity on their surface is also 1:2.? has been provided alongside types of If the density of two planets is the same,but their radii are in the ratio 1:2 ,prove that the ratio of acceleration due to gravity on their surface is also 1:2.? theory, EduRev gives you an
ample number of questions to practice If the density of two planets is the same,but their radii are in the ratio 1:2 ,prove that the ratio of acceleration due to gravity on their surface is also 1:2.? tests, examples and also practice Class 9 tests.

|
Explore Courses for Class 9 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























