Class 12 Exam > Class 12 Questions > A particle of mass m and charge q is in motio...
Start Learning for Free
A particle of mass m and charge q is in motion at speed v parallel to a long straight conductor carrying current I in positive X axis .find the direction and magnitude of electric field required so that the particle goes undeflected?
Most Upvoted Answer
A particle of mass m and charge q is in motion at speed v parallel to ...
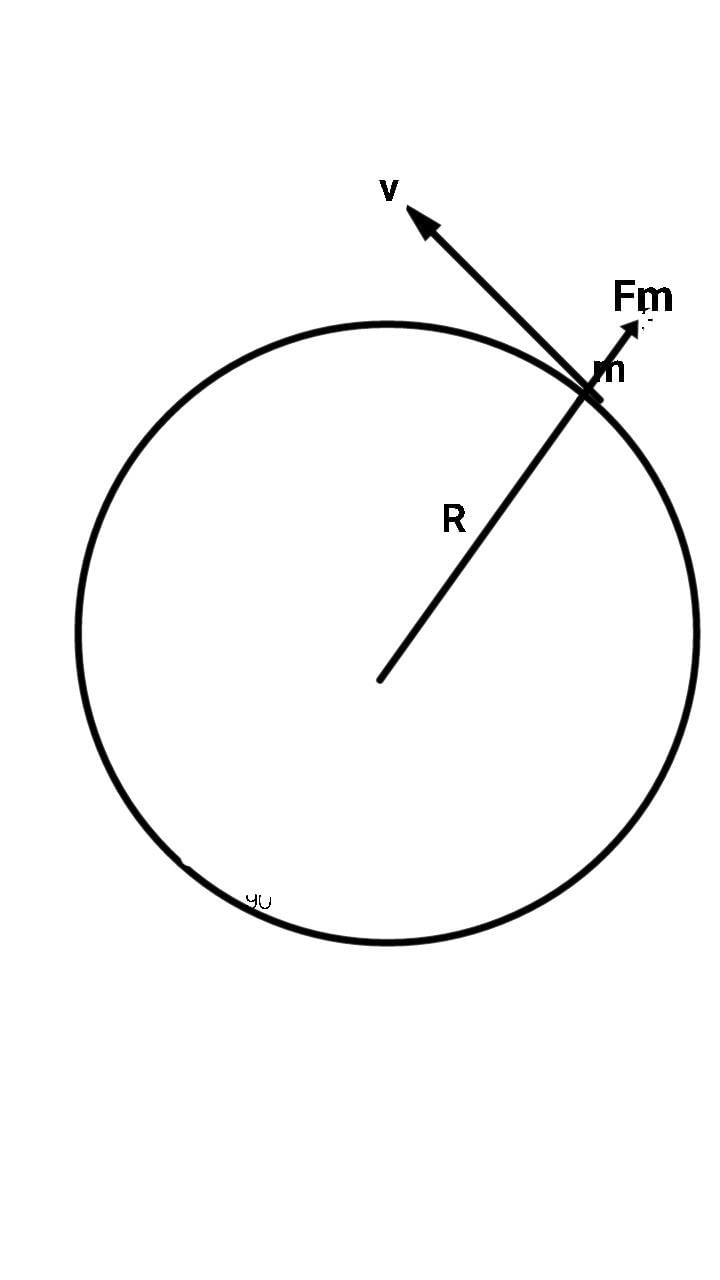
A particle of mass m and charge q is moving in a circular path with constant speed v in a perpendicular uniform magnetic field B as shown in figure .
force act on moving charged particle due to magnetic field B , Fm = Bqvsin90� = Bqv [because magnetic field and velocity of particle is perpendicular ]
now, at equilibrium ,
magnetic force, Fm = mv�/r
Bqv = mv�/r
r = mv/qB
now, time period , T = 2π/ω
also ω = v/r
ω = v/(mv/qB) = qB/m
now, Time period, T = 2π/(qB/m) = 2πm/qB
Hence, T = 2πm/qB
Community Answer
A particle of mass m and charge q is in motion at speed v parallel to ...
Introduction:
When a charged particle moves in a magnetic field, it experiences a force called the Lorentz force. This force can cause the particle to deviate from its original path. In order for the particle to go undeflected, an electric field can be applied in a specific direction and magnitude to counteract the magnetic force.
Key Concepts:
1. Lorentz force: The force experienced by a charged particle moving in a magnetic field is given by the equation F = q(v × B), where F is the force, q is the charge of the particle, v is its velocity, and B is the magnetic field.
2. Electric field: The force experienced by a charged particle in an electric field is given by the equation F = qE, where F is the force, q is the charge of the particle, and E is the electric field.
Analysis:
In this scenario, the charged particle is moving parallel to a long straight conductor carrying current I in the positive X-axis direction. To find the direction and magnitude of the electric field required for the particle to go undeflected, we need to determine the magnetic force acting on the particle and then apply an electric field to counteract this force.
The magnetic field produced by the current-carrying conductor can be determined using Ampere's Law. Since the conductor is straight and the current is flowing in the positive X-axis direction, the magnetic field will circulate around the conductor in a clockwise direction when viewed from above.
Steps:
1. Determine the direction of the magnetic field using the right-hand rule for a current-carrying conductor.
2. Use the Lorentz force equation F = q(v × B) to calculate the magnetic force acting on the particle.
3. Apply an electric field in the opposite direction to the Lorentz force to counteract it.
4. Calculate the magnitude of the electric field using the equation F = qE.
Conclusion:
By applying an electric field in the opposite direction to the Lorentz force acting on the charged particle, we can ensure that the particle goes undeflected. The magnitude of the electric field can be determined by equating the force due to the electric field to the Lorentz force. It is important to note that the direction and magnitude of the electric field may vary depending on the specific values of the charge, mass, velocity, and current in the system.
When a charged particle moves in a magnetic field, it experiences a force called the Lorentz force. This force can cause the particle to deviate from its original path. In order for the particle to go undeflected, an electric field can be applied in a specific direction and magnitude to counteract the magnetic force.
Key Concepts:
1. Lorentz force: The force experienced by a charged particle moving in a magnetic field is given by the equation F = q(v × B), where F is the force, q is the charge of the particle, v is its velocity, and B is the magnetic field.
2. Electric field: The force experienced by a charged particle in an electric field is given by the equation F = qE, where F is the force, q is the charge of the particle, and E is the electric field.
Analysis:
In this scenario, the charged particle is moving parallel to a long straight conductor carrying current I in the positive X-axis direction. To find the direction and magnitude of the electric field required for the particle to go undeflected, we need to determine the magnetic force acting on the particle and then apply an electric field to counteract this force.
The magnetic field produced by the current-carrying conductor can be determined using Ampere's Law. Since the conductor is straight and the current is flowing in the positive X-axis direction, the magnetic field will circulate around the conductor in a clockwise direction when viewed from above.
Steps:
1. Determine the direction of the magnetic field using the right-hand rule for a current-carrying conductor.
2. Use the Lorentz force equation F = q(v × B) to calculate the magnetic force acting on the particle.
3. Apply an electric field in the opposite direction to the Lorentz force to counteract it.
4. Calculate the magnitude of the electric field using the equation F = qE.
Conclusion:
By applying an electric field in the opposite direction to the Lorentz force acting on the charged particle, we can ensure that the particle goes undeflected. The magnitude of the electric field can be determined by equating the force due to the electric field to the Lorentz force. It is important to note that the direction and magnitude of the electric field may vary depending on the specific values of the charge, mass, velocity, and current in the system.

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
A particle of mass m and charge q is in motion at speed v parallel to a long straight conductor carrying current I in positive X axis .find the direction and magnitude of electric field required so that the particle goes undeflected?
Question Description
A particle of mass m and charge q is in motion at speed v parallel to a long straight conductor carrying current I in positive X axis .find the direction and magnitude of electric field required so that the particle goes undeflected? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A particle of mass m and charge q is in motion at speed v parallel to a long straight conductor carrying current I in positive X axis .find the direction and magnitude of electric field required so that the particle goes undeflected? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A particle of mass m and charge q is in motion at speed v parallel to a long straight conductor carrying current I in positive X axis .find the direction and magnitude of electric field required so that the particle goes undeflected?.
A particle of mass m and charge q is in motion at speed v parallel to a long straight conductor carrying current I in positive X axis .find the direction and magnitude of electric field required so that the particle goes undeflected? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A particle of mass m and charge q is in motion at speed v parallel to a long straight conductor carrying current I in positive X axis .find the direction and magnitude of electric field required so that the particle goes undeflected? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A particle of mass m and charge q is in motion at speed v parallel to a long straight conductor carrying current I in positive X axis .find the direction and magnitude of electric field required so that the particle goes undeflected?.
Solutions for A particle of mass m and charge q is in motion at speed v parallel to a long straight conductor carrying current I in positive X axis .find the direction and magnitude of electric field required so that the particle goes undeflected? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of A particle of mass m and charge q is in motion at speed v parallel to a long straight conductor carrying current I in positive X axis .find the direction and magnitude of electric field required so that the particle goes undeflected? defined & explained in the simplest way possible. Besides giving the explanation of
A particle of mass m and charge q is in motion at speed v parallel to a long straight conductor carrying current I in positive X axis .find the direction and magnitude of electric field required so that the particle goes undeflected?, a detailed solution for A particle of mass m and charge q is in motion at speed v parallel to a long straight conductor carrying current I in positive X axis .find the direction and magnitude of electric field required so that the particle goes undeflected? has been provided alongside types of A particle of mass m and charge q is in motion at speed v parallel to a long straight conductor carrying current I in positive X axis .find the direction and magnitude of electric field required so that the particle goes undeflected? theory, EduRev gives you an
ample number of questions to practice A particle of mass m and charge q is in motion at speed v parallel to a long straight conductor carrying current I in positive X axis .find the direction and magnitude of electric field required so that the particle goes undeflected? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















