Class 11 Exam > Class 11 Questions > How many cyclic isomers exists (structural an...
Start Learning for Free
How many cyclic isomers exists (structural and geometrical only) for C3H3CI3?
- a)2
- b)3
- c)4
- d)5
Correct answer is option 'B'. Can you explain this answer?
Verified Answer
How many cyclic isomers exists (structural and geometrical only) for C...
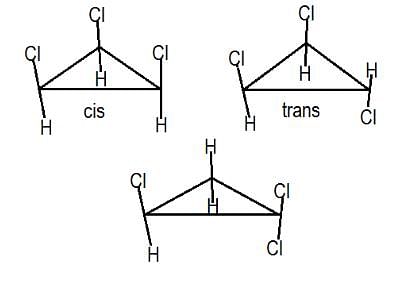
These 3 are the possible structures.
Hence, B is correct.
 This question is part of UPSC exam. View all Class 11 courses
This question is part of UPSC exam. View all Class 11 courses
Most Upvoted Answer
How many cyclic isomers exists (structural and geometrical only) for C...
Possible response:
Cyclic Isomers of C3H3Cl3
Cyclic isomers of a molecule are those that can be arranged in a ring or cycle, with the same number and types of atoms but different connectivity and/or orientation. For C3H3Cl3, we need to consider both structural and geometrical isomers, as there are three carbon-carbon double bonds and one chlorine atom attached to each carbon atom. We can use a systematic approach to generate all possible cyclic isomers, by varying the positions of the chlorine atoms and the orientation of the double bonds.
1. Draw the basic skeleton of the cyclic molecule, with three carbon atoms connected by double bonds, and one chlorine atom attached to each carbon atom. Label the atoms and bonds to keep track of them.
C=C-C=C-C
| | | |
Cl Cl Cl
2. Consider the possible arrangements of the three chlorine atoms. Since they are all equivalent, we can start with one of them and move it to the adjacent carbon atoms, one at a time, until we have gone around the ring.
a. Cl-C=C-C-Cl-C
b. Cl-C=C-Cl-C-C
c. Cl-C-Cl-C=C-C
d. C=C-Cl-C=C-Cl
e. C-Cl-C=C-Cl-C
3. For each of the three possible arrangements of the chlorine atoms, we need to examine the possible geometrical isomers, which depend on the relative positions of the two chlorine atoms attached to the same carbon atom. There are two possibilities: cis (on the same side) and trans (on opposite sides).
a. Cl-C=C-C-Cl-C (cis and trans)
b. Cl-C=C-Cl-C-C (cis and trans)
c. Cl-C-Cl-C=C-C (cis only, as the trans is not possible due to steric hindrance)
d. C=C-Cl-C=C-Cl (cis and trans)
e. C-Cl-C=C-Cl-C (cis and trans)
4. Count the number of distinct cyclic isomers. We can eliminate the ones that are mirror images or rotations of each other.
a. Cl-C=C-C-Cl-C (cis and trans)
b. Cl-C=C-Cl-C-C (cis and trans)
c. Cl-C-Cl-C=C-C (cis only)
d. C=C-Cl-C=C-Cl (cis and trans)
e. C-Cl-C=C-Cl-C (cis and trans)
Therefore, there are three structural isomers (a, b, and c) and two geometrical isomers (cis and trans) for each of them, giving a total of six isomers. However, some of them are identical, so the final answer is three cyclic isomers for C3H3Cl3.
Cyclic Isomers of C3H3Cl3
Cyclic isomers of a molecule are those that can be arranged in a ring or cycle, with the same number and types of atoms but different connectivity and/or orientation. For C3H3Cl3, we need to consider both structural and geometrical isomers, as there are three carbon-carbon double bonds and one chlorine atom attached to each carbon atom. We can use a systematic approach to generate all possible cyclic isomers, by varying the positions of the chlorine atoms and the orientation of the double bonds.
1. Draw the basic skeleton of the cyclic molecule, with three carbon atoms connected by double bonds, and one chlorine atom attached to each carbon atom. Label the atoms and bonds to keep track of them.
C=C-C=C-C
| | | |
Cl Cl Cl
2. Consider the possible arrangements of the three chlorine atoms. Since they are all equivalent, we can start with one of them and move it to the adjacent carbon atoms, one at a time, until we have gone around the ring.
a. Cl-C=C-C-Cl-C
b. Cl-C=C-Cl-C-C
c. Cl-C-Cl-C=C-C
d. C=C-Cl-C=C-Cl
e. C-Cl-C=C-Cl-C
3. For each of the three possible arrangements of the chlorine atoms, we need to examine the possible geometrical isomers, which depend on the relative positions of the two chlorine atoms attached to the same carbon atom. There are two possibilities: cis (on the same side) and trans (on opposite sides).
a. Cl-C=C-C-Cl-C (cis and trans)
b. Cl-C=C-Cl-C-C (cis and trans)
c. Cl-C-Cl-C=C-C (cis only, as the trans is not possible due to steric hindrance)
d. C=C-Cl-C=C-Cl (cis and trans)
e. C-Cl-C=C-Cl-C (cis and trans)
4. Count the number of distinct cyclic isomers. We can eliminate the ones that are mirror images or rotations of each other.
a. Cl-C=C-C-Cl-C (cis and trans)
b. Cl-C=C-Cl-C-C (cis and trans)
c. Cl-C-Cl-C=C-C (cis only)
d. C=C-Cl-C=C-Cl (cis and trans)
e. C-Cl-C=C-Cl-C (cis and trans)
Therefore, there are three structural isomers (a, b, and c) and two geometrical isomers (cis and trans) for each of them, giving a total of six isomers. However, some of them are identical, so the final answer is three cyclic isomers for C3H3Cl3.
Community Answer
How many cyclic isomers exists (structural and geometrical only) for C...
Attention Class 11 Students!
To make sure you are not studying endlessly, EduRev has designed Class 11 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 11.

|
Explore Courses for Class 11 exam
|

|
Similar Class 11 Doubts
How many cyclic isomers exists (structural and geometrical only) for C3H3CI3?a)2b)3c)4d)5Correct answer is option 'B'. Can you explain this answer?
Question Description
How many cyclic isomers exists (structural and geometrical only) for C3H3CI3?a)2b)3c)4d)5Correct answer is option 'B'. Can you explain this answer? for Class 11 2024 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about How many cyclic isomers exists (structural and geometrical only) for C3H3CI3?a)2b)3c)4d)5Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Class 11 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for How many cyclic isomers exists (structural and geometrical only) for C3H3CI3?a)2b)3c)4d)5Correct answer is option 'B'. Can you explain this answer?.
How many cyclic isomers exists (structural and geometrical only) for C3H3CI3?a)2b)3c)4d)5Correct answer is option 'B'. Can you explain this answer? for Class 11 2024 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about How many cyclic isomers exists (structural and geometrical only) for C3H3CI3?a)2b)3c)4d)5Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Class 11 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for How many cyclic isomers exists (structural and geometrical only) for C3H3CI3?a)2b)3c)4d)5Correct answer is option 'B'. Can you explain this answer?.
Solutions for How many cyclic isomers exists (structural and geometrical only) for C3H3CI3?a)2b)3c)4d)5Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of How many cyclic isomers exists (structural and geometrical only) for C3H3CI3?a)2b)3c)4d)5Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
How many cyclic isomers exists (structural and geometrical only) for C3H3CI3?a)2b)3c)4d)5Correct answer is option 'B'. Can you explain this answer?, a detailed solution for How many cyclic isomers exists (structural and geometrical only) for C3H3CI3?a)2b)3c)4d)5Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of How many cyclic isomers exists (structural and geometrical only) for C3H3CI3?a)2b)3c)4d)5Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice How many cyclic isomers exists (structural and geometrical only) for C3H3CI3?a)2b)3c)4d)5Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice Class 11 tests.

|
Explore Courses for Class 11 exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























