Class 12 Exam > Class 12 Questions > Calculate the radius of a water drop which wo...
Start Learning for Free
Calculate the radius of a water drop which would just remain suspended in the earth's electric field of 300 V/m when charged with one electron?
Most Upvoted Answer
Calculate the radius of a water drop which would just remain suspended...
Calculating the radius of a water drop suspended in the earth's electric field:
To calculate the radius of a water drop that would remain suspended in the earth's electric field of 300 V/m when charged with one electron, we need to use the formula for the electric force on a charged particle in an electric field.
The formula is:
F = qE
Where F is the electric force, q is the charge on the particle, and E is the electric field.
Step 1: Calculate the electric force on a single electron in the earth's electric field of 300 V/m.
We know that the charge on a single electron is -1.6 x 10^-19 Coulombs, and the electric field in this case is 300 V/m.
Plugging these values into the formula, we get:
F = (-1.6 x 10^-19 C) x (300 V/m) = -4.8 x 10^-17 N
The negative sign indicates that the force is acting in the opposite direction to the electric field.
Step 2: Calculate the weight of the water droplet.
To determine the radius of the water droplet, we need to know its weight. For simplicity, we will assume that the droplet is a perfect sphere and calculate the weight using the formula:
W = (4/3)πr^3ρg
Where W is the weight, r is the radius, ρ is the density of water, and g is the acceleration due to gravity.
Assuming a density of 1000 kg/m^3 for water, and an acceleration due to gravity of 9.8 m/s^2, we get:
W = (4/3)πr^3(1000)(9.8) = 41.2r^3 N
Step 3: Equate the electric force on the electron with the weight of the water droplet.
Since the droplet is in equilibrium, the electric force on the electron must be equal and opposite to the weight of the droplet. Therefore, we can equate the two forces and solve for the radius of the droplet:
-4.8 x 10^-17 N = 41.2r^3 N
r^3 = (-4.8 x 10^-17 N) / (41.2 N)
r^3 = -1.166 x 10^-18 m^3
Taking the cube root of both sides, we get:
r = 2.8 x 10^-7 m
Therefore, the radius of the water droplet that would remain suspended in the earth's electric field of 300 V/m when charged with one electron is approximately 2.8 x 10^-7 m.
Explanation:
The electric field in the earth's atmosphere is caused by the separation of positive and negative charges in the atmosphere. When a water droplet is charged with one electron, it experiences an electric force in the opposite direction to the electric field. If this force is equal and opposite to the weight of the droplet, the droplet will remain suspended in the air. By equating the electric force on the electron with the weight of the droplet, we can calculate the radius of the droplet that would remain suspended in the electric field.
To calculate the radius of a water drop that would remain suspended in the earth's electric field of 300 V/m when charged with one electron, we need to use the formula for the electric force on a charged particle in an electric field.
The formula is:
F = qE
Where F is the electric force, q is the charge on the particle, and E is the electric field.
Step 1: Calculate the electric force on a single electron in the earth's electric field of 300 V/m.
We know that the charge on a single electron is -1.6 x 10^-19 Coulombs, and the electric field in this case is 300 V/m.
Plugging these values into the formula, we get:
F = (-1.6 x 10^-19 C) x (300 V/m) = -4.8 x 10^-17 N
The negative sign indicates that the force is acting in the opposite direction to the electric field.
Step 2: Calculate the weight of the water droplet.
To determine the radius of the water droplet, we need to know its weight. For simplicity, we will assume that the droplet is a perfect sphere and calculate the weight using the formula:
W = (4/3)πr^3ρg
Where W is the weight, r is the radius, ρ is the density of water, and g is the acceleration due to gravity.
Assuming a density of 1000 kg/m^3 for water, and an acceleration due to gravity of 9.8 m/s^2, we get:
W = (4/3)πr^3(1000)(9.8) = 41.2r^3 N
Step 3: Equate the electric force on the electron with the weight of the water droplet.
Since the droplet is in equilibrium, the electric force on the electron must be equal and opposite to the weight of the droplet. Therefore, we can equate the two forces and solve for the radius of the droplet:
-4.8 x 10^-17 N = 41.2r^3 N
r^3 = (-4.8 x 10^-17 N) / (41.2 N)
r^3 = -1.166 x 10^-18 m^3
Taking the cube root of both sides, we get:
r = 2.8 x 10^-7 m
Therefore, the radius of the water droplet that would remain suspended in the earth's electric field of 300 V/m when charged with one electron is approximately 2.8 x 10^-7 m.
Explanation:
The electric field in the earth's atmosphere is caused by the separation of positive and negative charges in the atmosphere. When a water droplet is charged with one electron, it experiences an electric force in the opposite direction to the electric field. If this force is equal and opposite to the weight of the droplet, the droplet will remain suspended in the air. By equating the electric force on the electron with the weight of the droplet, we can calculate the radius of the droplet that would remain suspended in the electric field.
Community Answer
Calculate the radius of a water drop which would just remain suspended...
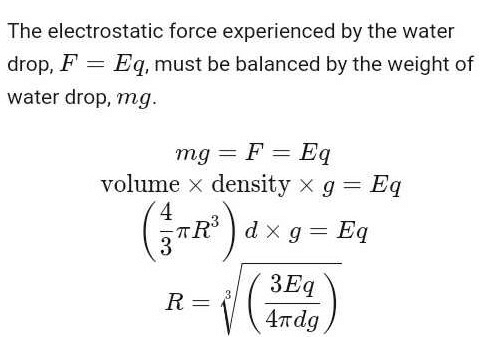

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
Calculate the radius of a water drop which would just remain suspended in the earth's electric field of 300 V/m when charged with one electron?
Question Description
Calculate the radius of a water drop which would just remain suspended in the earth's electric field of 300 V/m when charged with one electron? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Calculate the radius of a water drop which would just remain suspended in the earth's electric field of 300 V/m when charged with one electron? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Calculate the radius of a water drop which would just remain suspended in the earth's electric field of 300 V/m when charged with one electron?.
Calculate the radius of a water drop which would just remain suspended in the earth's electric field of 300 V/m when charged with one electron? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Calculate the radius of a water drop which would just remain suspended in the earth's electric field of 300 V/m when charged with one electron? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Calculate the radius of a water drop which would just remain suspended in the earth's electric field of 300 V/m when charged with one electron?.
Solutions for Calculate the radius of a water drop which would just remain suspended in the earth's electric field of 300 V/m when charged with one electron? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of Calculate the radius of a water drop which would just remain suspended in the earth's electric field of 300 V/m when charged with one electron? defined & explained in the simplest way possible. Besides giving the explanation of
Calculate the radius of a water drop which would just remain suspended in the earth's electric field of 300 V/m when charged with one electron?, a detailed solution for Calculate the radius of a water drop which would just remain suspended in the earth's electric field of 300 V/m when charged with one electron? has been provided alongside types of Calculate the radius of a water drop which would just remain suspended in the earth's electric field of 300 V/m when charged with one electron? theory, EduRev gives you an
ample number of questions to practice Calculate the radius of a water drop which would just remain suspended in the earth's electric field of 300 V/m when charged with one electron? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















