Class 9 Exam > Class 9 Questions > what is meant by integration and differentiat...
Start Learning for Free
what is meant by integration and differentiation
Verified Answer
what is meant by integration and differentiation
Suppose you need to find the slope of the tangent line to a graph at point P. The slope can be approximated by drawing a line through the point P and finding the slope by a line that is known as secant line.A function f in x is said to be differentiable at the point x = a if the derivative f'(a) exists at every point in its domain. The differentiation formula is given by:
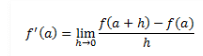
For a function to be differentiable at any point x=a in its domain, it must be continuous at that particular point but vice-versa is necessarily not always true. The domain of f’(x) is defined by the existence of its limits.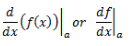
If y = f(x) is a function in x, then the derivative of f(x) is given as dy/dx . This is known as the derivative of y with respect to x.
Also, the derivative of a function f in x at x = a is given as:
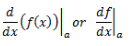
Derivative of a function f(x) signifies the rate of change of the function f(x) with respect to x at a point a lying in its domain.
If the derivative of the function, f’, is known which is differentiable in its domain then we can find the function f. In integral calculus, we call f as the anti-derivative or primitive of the function f’. The method of calculating the anti-derivative is known as anti-differentiation or integration.
Integration Rules
The integration of a function f(x) is given by F(x) and it is represented by: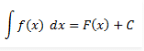 
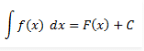
where
R.H.S. of the equation indicates integral of f(x) with respect to x
F(x) is called anti-derivative or primitive.
f(x) is called the integrand.
dx is called the integrating agent.
C is the constant of integration or arbitrary constant.
x is the variable of integration.
From the above discussion, it can be said that differentiation and integration are the reverse processes of each other. Both differentiation and integration are operations which are performed on functions.
This question is part of UPSC exam. View all Class 9 courses
Most Upvoted Answer
what is meant by integration and differentiation
Integration and Differentiation
Integration and differentiation are fundamental concepts in calculus that involve the manipulation of functions to find new functions or relationships between quantities.
Integration:
- Integration is the process of finding the integral of a function. It involves finding the area under a curve or the accumulation of quantities over a given interval.
- The result of integration is an antiderivative, which represents the original function up to a constant.
- The symbol used for integration is the integral sign (∫), and the process is also known as finding the primitive function of a given function.
- Integration is used in various fields such as physics, engineering, and economics to calculate quantities like displacement, velocity, and area.
Differentiation:
- Differentiation is the process of finding the derivative of a function. It involves calculating the rate of change or slope of a function at a given point.
- The derivative represents the instantaneous rate of change of a function at a specific point.
- The symbol used for differentiation is the derivative sign (d/dx or f'(x)), and the process is also known as finding the slope of a curve.
- Differentiation is used to solve problems involving optimization, finding maximum and minimum values, and determining the behavior of functions.
In conclusion, integration and differentiation are two sides of the same coin in calculus. Integration focuses on finding the area under a curve or accumulation of quantities, while differentiation deals with finding the rate of change or slope of a function. Both concepts are essential tools for analyzing functions and solving a wide range of mathematical and real-world problems.
Integration and differentiation are fundamental concepts in calculus that involve the manipulation of functions to find new functions or relationships between quantities.
Integration:
- Integration is the process of finding the integral of a function. It involves finding the area under a curve or the accumulation of quantities over a given interval.
- The result of integration is an antiderivative, which represents the original function up to a constant.
- The symbol used for integration is the integral sign (∫), and the process is also known as finding the primitive function of a given function.
- Integration is used in various fields such as physics, engineering, and economics to calculate quantities like displacement, velocity, and area.
Differentiation:
- Differentiation is the process of finding the derivative of a function. It involves calculating the rate of change or slope of a function at a given point.
- The derivative represents the instantaneous rate of change of a function at a specific point.
- The symbol used for differentiation is the derivative sign (d/dx or f'(x)), and the process is also known as finding the slope of a curve.
- Differentiation is used to solve problems involving optimization, finding maximum and minimum values, and determining the behavior of functions.
In conclusion, integration and differentiation are two sides of the same coin in calculus. Integration focuses on finding the area under a curve or accumulation of quantities, while differentiation deals with finding the rate of change or slope of a function. Both concepts are essential tools for analyzing functions and solving a wide range of mathematical and real-world problems.
Attention Class 9 Students!
To make sure you are not studying endlessly, EduRev has designed Class 9 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 9.
|
|
Explore Courses for Class 9 exam
|
|
Top Courses for Class 9View all
what is meant by integration and differentiation
Question Description
what is meant by integration and differentiation for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about what is meant by integration and differentiation covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for what is meant by integration and differentiation.
what is meant by integration and differentiation for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about what is meant by integration and differentiation covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for what is meant by integration and differentiation.
Solutions for what is meant by integration and differentiation in English & in Hindi are available as part of our courses for Class 9.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Here you can find the meaning of what is meant by integration and differentiation defined & explained in the simplest way possible. Besides giving the explanation of
what is meant by integration and differentiation, a detailed solution for what is meant by integration and differentiation has been provided alongside types of what is meant by integration and differentiation theory, EduRev gives you an
ample number of questions to practice what is meant by integration and differentiation tests, examples and also practice Class 9 tests.
|
|
Explore Courses for Class 9 exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup