8.XY is a line parallel to side BC of a triangle ABC. If BE -- AC and CF -- AB meet XY at E and F respectively, show that ar ABE = ar ACF?

Explore Courses UPSC Exam UPSC Test Series Free Notes EduRev Infinity

Open App

Class 9 Exam > Class 9 Questions > 8.XY is a line parallel to side BC of a trian...

Join the Discussion on the App

8.XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar ABE = ar ACF?

Join for Free

Join for Free

Verified Answer

8.XY is a line parallel to side BC of a triangle ABC. If BE || AC and ...

To Prove: ar(ΔABE) = ar(ΔACF).

Proof: ∵ XY || BC | given

and CF || BX | ∵ CF || AB (given)

∴ □BCFX is a || gm

A quadrilateral is a parallelogram if its opposite sides are parallel

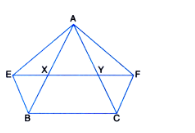
∴ BC = XF

| Opposite sides of a parallelogram are equal ⇒ BC = XY + YF ...(1)

Again,

∵ XY || BC | given

and BE || CY | ∵ BE || AC (given)

∴ □BCYE is a parallelogram

A quadrilateral is a parallelogram if its opposite sides are parallel

∴ BC = YE

| Opposite sides of a parallelogram are equal

⇒ BC = XY + XE ...(2)

From (1) and (2),

XY + YF = XY + XE

⇒ YF = XE

⇒ XE = YF ...(3)

∵ ΔAEX and ΔAYF have equal bases (∵ XE = YF) on the same line EF and have a common vertex A.

∴ Their altitudes are also the same.

∴ ar(ΔAEX) = ar(ΔAFY) ...(4)

∵ ΔBEX and ΔCFY have equal bases (∵ XE = YF) on the same line EF and are between the same parallels EF and BC (∵ XY || BC).

∴ ar(ΔBEX) = ar(ΔCFY) ...(5)

Two triangles on the same base (or equal bases) and between the same parallels are equal in area

Adding the corresponding sides of (4) and (5), we get

ar(ΔAEX) + ar(ΔBEX) = ar(ΔAFY) + ar(ΔCFY)

⇒ ar(ΔABE) = ar(⇒ACF).

This question is part of UPSC exam. View all Class 9 courses

View all answers Start learning for free

Explore Courses for Class 9 exam

Similar Class 9 Doubts

the sides ab and ac of a triangle ABC are produced to P and Q respectively. if the bisector of angle abc and angle ACB intersected at then prove that is equal to angle BOC is equal to 90 minus half angle A Related: Hots Questions- Triangles?

View answer

P,q &r are the mid points of the sides BC, CA and AB respectively of a triangle ABC .PR and BQ meet at X, CR and PQ meet at Y . Prove that XY=1/4BC.?

View answer

ABC is a triangle and througg A,B,C lines are drawn parallel to BC ,CA and AB respectively intersecting at P,Q and R .prove that the perimeter of triangle PQR is double the perimeter of triangleABC?

View answer

The bisectors of base angles q and R of an equilateral triangle pqr intersect at point S. ST and smdrawn parallel to the sides PQ and PR intersecting side q r at t and M respectively prove that QT = cm equals Mr?

View answer

Top Courses for Class 9View all

Top Courses for Class 9

View all

8.XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar ABE = ar ACF?

Share with a Friend

Answer this doubt

Question Description
8.XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar ABE = ar ACF? for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about 8.XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar ABE = ar ACF? covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for 8.XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar ABE = ar ACF?.

Solutions for 8.XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar ABE = ar ACF? in English & in Hindi are available as part of our courses for Class 9. Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.

Here you can find the meaning of 8.XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar ABE = ar ACF? defined & explained in the simplest way possible. Besides giving the explanation of 8.XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar ABE = ar ACF?, a detailed solution for 8.XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar ABE = ar ACF? has been provided alongside types of 8.XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar ABE = ar ACF? theory, EduRev gives you an ample number of questions to practice 8.XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar ABE = ar ACF? tests, examples and also practice Class 9 tests.

Explore Courses for Class 9 exam