Class 9 Exam > Class 9 Questions > If two equal chords of a circle intersect wit...
Start Learning for Free
If two equal chords of a circle intersect within the circle prove that the line joining the point of intersection to the center makes equal angles withe the chord.
Verified Answer
If two equal chords of a circle intersect within the circle prove that...
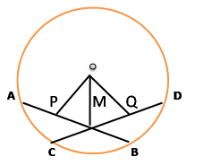
Let AB and CD are the two equal chords of a circle having center O
Again let AB and CD intersect each other at a point M.
Now, draw OP perpendicular AB and OQ perpendicular CD
From the figure,
In ΔOPM and ΔOQM,
OP = OQ {equal chords are equally distant from the cntre}
∠OPM = ∠OQM
OM = OM {common}
By SAS congruence criterion,
ΔOPM ≅ ΔOQM
So, ∠OMA = ∠OMD
or ∠OMP = ∠OMQ {by CPCT}
 This question is part of UPSC exam. View all Class 9 courses
This question is part of UPSC exam. View all Class 9 courses

|
Explore Courses for Class 9 exam
|

|
Similar Class 9 Doubts
If two equal chords of a circle intersect within the circle prove that the line joining the point of intersection to the center makes equal angles withe the chord. Related: Angles Related to a Circle - Mathematics, Class 9
Question Description
If two equal chords of a circle intersect within the circle prove that the line joining the point of intersection to the center makes equal angles withe the chord. Related: Angles Related to a Circle - Mathematics, Class 9 for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about If two equal chords of a circle intersect within the circle prove that the line joining the point of intersection to the center makes equal angles withe the chord. Related: Angles Related to a Circle - Mathematics, Class 9 covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If two equal chords of a circle intersect within the circle prove that the line joining the point of intersection to the center makes equal angles withe the chord. Related: Angles Related to a Circle - Mathematics, Class 9.
If two equal chords of a circle intersect within the circle prove that the line joining the point of intersection to the center makes equal angles withe the chord. Related: Angles Related to a Circle - Mathematics, Class 9 for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about If two equal chords of a circle intersect within the circle prove that the line joining the point of intersection to the center makes equal angles withe the chord. Related: Angles Related to a Circle - Mathematics, Class 9 covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If two equal chords of a circle intersect within the circle prove that the line joining the point of intersection to the center makes equal angles withe the chord. Related: Angles Related to a Circle - Mathematics, Class 9.
Solutions for If two equal chords of a circle intersect within the circle prove that the line joining the point of intersection to the center makes equal angles withe the chord. Related: Angles Related to a Circle - Mathematics, Class 9 in English & in Hindi are available as part of our courses for Class 9.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Here you can find the meaning of If two equal chords of a circle intersect within the circle prove that the line joining the point of intersection to the center makes equal angles withe the chord. Related: Angles Related to a Circle - Mathematics, Class 9 defined & explained in the simplest way possible. Besides giving the explanation of
If two equal chords of a circle intersect within the circle prove that the line joining the point of intersection to the center makes equal angles withe the chord. Related: Angles Related to a Circle - Mathematics, Class 9, a detailed solution for If two equal chords of a circle intersect within the circle prove that the line joining the point of intersection to the center makes equal angles withe the chord. Related: Angles Related to a Circle - Mathematics, Class 9 has been provided alongside types of If two equal chords of a circle intersect within the circle prove that the line joining the point of intersection to the center makes equal angles withe the chord. Related: Angles Related to a Circle - Mathematics, Class 9 theory, EduRev gives you an
ample number of questions to practice If two equal chords of a circle intersect within the circle prove that the line joining the point of intersection to the center makes equal angles withe the chord. Related: Angles Related to a Circle - Mathematics, Class 9 tests, examples and also practice Class 9 tests.

|
Explore Courses for Class 9 exam
|

|
Suggested Free Tests
Test: The Fundamental Unit of Life- Case Based Type Questions- 1
Test | 10 questions
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























