Class 11 Exam > Class 11 Questions > A ray of light is deviated by 90 degree by a ...
Start Learning for Free
A ray of light is deviated by 90 degree by a right isosceles prism. What should be the minimum refractive index of material of prism?
Verified Answer
A ray of light is deviated by 90 degree by a right isosceles prism. Wh...
A light beam, falling on one of the two face of a 90degree angle prism, at A will enter the prism without any deviation. Then it will hit the hypotenuse at θ = 45degree, going from an optically dense material with RE np to an optically lighter material, air.
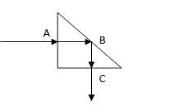


If nα and np are the refractive indexes of air (= 1) and prism (= ??), the minimum RE is found when the angle of reflection on the hypotenuse on B, θ, (= 45degree) is equal at least to the critical angle θc

 This question is part of UPSC exam. View all Class 11 courses
This question is part of UPSC exam. View all Class 11 courses
Most Upvoted Answer
A ray of light is deviated by 90 degree by a right isosceles prism. Wh...
Introduction:
When a ray of light passes through a prism, it undergoes refraction, which causes it to change direction. The amount of deviation depends on the refractive index of the material of the prism. In this case, we have a right isosceles prism that deviates the ray of light by 90 degrees. We need to determine the minimum refractive index of the prism's material to achieve this deviation.
Understanding refraction:
Refraction occurs when light passes from one medium to another, and its speed changes. The change in speed causes the light ray to bend. The amount of bending depends on the refractive indices of the two media involved. The refractive index (n) of a material is the ratio of the speed of light in a vacuum (c) to the speed of light in that material (v): n = c/v.
Deviation by a right isosceles prism:
A right isosceles prism is a prism with a right angle between its two equal faces. When a ray of light enters such a prism perpendicular to one of its faces, it undergoes two refractions and one total internal reflection. The deviation caused by this prism depends on the refractive index of the material.
Minimum refractive index for 90-degree deviation:
To achieve a 90-degree deviation, the incoming ray of light should be incident at the critical angle. The critical angle (θc) is the angle of incidence at which the refracted ray travels along the interface between the two media. For a right isosceles prism, the critical angle occurs at the interface between the prism and air.
Calculating the minimum refractive index:
The critical angle (θc) can be calculated using the formula: sin(θc) = 1/n, where n is the refractive index of the prism's material. For a 90-degree deviation, the critical angle is 45 degrees.
To find the minimum refractive index, we can rearrange the formula as: n = 1/sin(θc).
Using the critical angle of 45 degrees, we can substitute it into the equation:
n = 1/sin(45°) = 1/√2 ≈ 0.707.
Therefore, the minimum refractive index of the prism's material should be approximately 0.707 to achieve a 90-degree deviation.
Conclusion:
In conclusion, for a ray of light to be deviated by 90 degrees in a right isosceles prism, the minimum refractive index of the prism's material should be approximately 0.707. This can be achieved by ensuring the incident angle of the ray is at the critical angle, which is 45 degrees in this case.
When a ray of light passes through a prism, it undergoes refraction, which causes it to change direction. The amount of deviation depends on the refractive index of the material of the prism. In this case, we have a right isosceles prism that deviates the ray of light by 90 degrees. We need to determine the minimum refractive index of the prism's material to achieve this deviation.
Understanding refraction:
Refraction occurs when light passes from one medium to another, and its speed changes. The change in speed causes the light ray to bend. The amount of bending depends on the refractive indices of the two media involved. The refractive index (n) of a material is the ratio of the speed of light in a vacuum (c) to the speed of light in that material (v): n = c/v.
Deviation by a right isosceles prism:
A right isosceles prism is a prism with a right angle between its two equal faces. When a ray of light enters such a prism perpendicular to one of its faces, it undergoes two refractions and one total internal reflection. The deviation caused by this prism depends on the refractive index of the material.
Minimum refractive index for 90-degree deviation:
To achieve a 90-degree deviation, the incoming ray of light should be incident at the critical angle. The critical angle (θc) is the angle of incidence at which the refracted ray travels along the interface between the two media. For a right isosceles prism, the critical angle occurs at the interface between the prism and air.
Calculating the minimum refractive index:
The critical angle (θc) can be calculated using the formula: sin(θc) = 1/n, where n is the refractive index of the prism's material. For a 90-degree deviation, the critical angle is 45 degrees.
To find the minimum refractive index, we can rearrange the formula as: n = 1/sin(θc).
Using the critical angle of 45 degrees, we can substitute it into the equation:
n = 1/sin(45°) = 1/√2 ≈ 0.707.
Therefore, the minimum refractive index of the prism's material should be approximately 0.707 to achieve a 90-degree deviation.
Conclusion:
In conclusion, for a ray of light to be deviated by 90 degrees in a right isosceles prism, the minimum refractive index of the prism's material should be approximately 0.707. This can be achieved by ensuring the incident angle of the ray is at the critical angle, which is 45 degrees in this case.
Attention Class 11 Students!
To make sure you are not studying endlessly, EduRev has designed Class 11 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 11.

|
Explore Courses for Class 11 exam
|

|
Similar Class 11 Doubts
A ray of light is deviated by 90 degree by a right isosceles prism. What should be the minimum refractive index of material of prism?
Question Description
A ray of light is deviated by 90 degree by a right isosceles prism. What should be the minimum refractive index of material of prism? for Class 11 2024 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about A ray of light is deviated by 90 degree by a right isosceles prism. What should be the minimum refractive index of material of prism? covers all topics & solutions for Class 11 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A ray of light is deviated by 90 degree by a right isosceles prism. What should be the minimum refractive index of material of prism?.
A ray of light is deviated by 90 degree by a right isosceles prism. What should be the minimum refractive index of material of prism? for Class 11 2024 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about A ray of light is deviated by 90 degree by a right isosceles prism. What should be the minimum refractive index of material of prism? covers all topics & solutions for Class 11 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A ray of light is deviated by 90 degree by a right isosceles prism. What should be the minimum refractive index of material of prism?.
Solutions for A ray of light is deviated by 90 degree by a right isosceles prism. What should be the minimum refractive index of material of prism? in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of A ray of light is deviated by 90 degree by a right isosceles prism. What should be the minimum refractive index of material of prism? defined & explained in the simplest way possible. Besides giving the explanation of
A ray of light is deviated by 90 degree by a right isosceles prism. What should be the minimum refractive index of material of prism?, a detailed solution for A ray of light is deviated by 90 degree by a right isosceles prism. What should be the minimum refractive index of material of prism? has been provided alongside types of A ray of light is deviated by 90 degree by a right isosceles prism. What should be the minimum refractive index of material of prism? theory, EduRev gives you an
ample number of questions to practice A ray of light is deviated by 90 degree by a right isosceles prism. What should be the minimum refractive index of material of prism? tests, examples and also practice Class 11 tests.

|
Explore Courses for Class 11 exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























