Computer Science Engineering (CSE) Exam > Computer Science Engineering (CSE) Questions > Consider an interpolation search which is an ...
Start Learning for Free
Consider an interpolation search which is an improvement over binary search where the values in a sorted array are uniformly distributed. In interpolation search construction of new data points take place at different locations according to the value of the key being searched. Find the time complexity of interpolation search.
- a)O(log n)
- b)O(n)
- c)O(n log n)
- d)O(log(log n))
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Consider an interpolation search which is an improvement over binary s...
To narrow down the search space binary search uses mid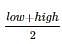 
while interpolation search uses mid =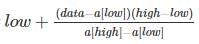 
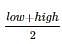while interpolation search uses mid =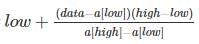 On average the interpolation search makes about log (log n) comparisons if the elements are uniformly distributed, where n is the number of elements to be searched.
Most Upvoted Answer
Consider an interpolation search which is an improvement over binary s...
The time complexity of interpolation search is O(log(log n)).
Interpolation search is an improvement over binary search, especially when the values in a sorted array are uniformly distributed. In binary search, the middle element of the sorted array is chosen as the pivot in each iteration. However, in interpolation search, the pivot is chosen based on the value of the key being searched. This allows for a more efficient search in cases where the values are uniformly distributed.
The algorithm for interpolation search can be summarized as follows:
1. Initialize the low and high indices of the array to search.
2. Calculate the position of the pivot using the formula:
pivot = low + ((key - array[low]) * (high - low)) / (array[high] - array[low])
This formula is used to estimate the position of the key in the sorted array based on its value and the distribution of the array values.
3. If the pivot is equal to the key, return the index of the pivot.
4. If the pivot is less than the key, update the low index to pivot + 1 and repeat step 2.
5. If the pivot is greater than the key, update the high index to pivot - 1 and repeat step 2.
6. Repeat steps 2-5 until the key is found or the search range is exhausted.
The time complexity of interpolation search can be analyzed by considering the worst-case scenario. In the worst case, the key being searched is either the minimum or maximum value in the array, or it is not present in the array at all.
In the worst case, the interpolation search algorithm reduces the search range by a constant factor in each iteration. This is because the pivot is calculated based on the value of the key and the distribution of the array values. As a result, the search range is reduced exponentially as the iterations progress.
Therefore, the number of iterations required to find the key in the worst case can be expressed as log(log n), where n is the size of the array. This is because each iteration reduces the search range by a constant factor, resulting in a logarithmic time complexity.
Hence, the time complexity of interpolation search is O(log(log n)).
Interpolation search is an improvement over binary search, especially when the values in a sorted array are uniformly distributed. In binary search, the middle element of the sorted array is chosen as the pivot in each iteration. However, in interpolation search, the pivot is chosen based on the value of the key being searched. This allows for a more efficient search in cases where the values are uniformly distributed.
The algorithm for interpolation search can be summarized as follows:
1. Initialize the low and high indices of the array to search.
2. Calculate the position of the pivot using the formula:
pivot = low + ((key - array[low]) * (high - low)) / (array[high] - array[low])
This formula is used to estimate the position of the key in the sorted array based on its value and the distribution of the array values.
3. If the pivot is equal to the key, return the index of the pivot.
4. If the pivot is less than the key, update the low index to pivot + 1 and repeat step 2.
5. If the pivot is greater than the key, update the high index to pivot - 1 and repeat step 2.
6. Repeat steps 2-5 until the key is found or the search range is exhausted.
The time complexity of interpolation search can be analyzed by considering the worst-case scenario. In the worst case, the key being searched is either the minimum or maximum value in the array, or it is not present in the array at all.
In the worst case, the interpolation search algorithm reduces the search range by a constant factor in each iteration. This is because the pivot is calculated based on the value of the key and the distribution of the array values. As a result, the search range is reduced exponentially as the iterations progress.
Therefore, the number of iterations required to find the key in the worst case can be expressed as log(log n), where n is the size of the array. This is because each iteration reduces the search range by a constant factor, resulting in a logarithmic time complexity.
Hence, the time complexity of interpolation search is O(log(log n)).
Attention Computer Science Engineering (CSE) Students!
To make sure you are not studying endlessly, EduRev has designed Computer Science Engineering (CSE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Computer Science Engineering (CSE).
|
Explore Courses for Computer Science Engineering (CSE) exam
|
|
Top Courses for Computer Science Engineering (CSE)View all
Consider an interpolation search which is an improvement over binary search where the values in a sorted array are uniformly distributed. In interpolation search construction of new data points take place at different locations according to the value of the key being searched. Find the time complexity of interpolation search.a)O(log n)b)O(n)c)O(n log n)d)O(log(log n))Correct answer is option 'D'. Can you explain this answer?
Question Description
Consider an interpolation search which is an improvement over binary search where the values in a sorted array are uniformly distributed. In interpolation search construction of new data points take place at different locations according to the value of the key being searched. Find the time complexity of interpolation search.a)O(log n)b)O(n)c)O(n log n)d)O(log(log n))Correct answer is option 'D'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Consider an interpolation search which is an improvement over binary search where the values in a sorted array are uniformly distributed. In interpolation search construction of new data points take place at different locations according to the value of the key being searched. Find the time complexity of interpolation search.a)O(log n)b)O(n)c)O(n log n)d)O(log(log n))Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider an interpolation search which is an improvement over binary search where the values in a sorted array are uniformly distributed. In interpolation search construction of new data points take place at different locations according to the value of the key being searched. Find the time complexity of interpolation search.a)O(log n)b)O(n)c)O(n log n)d)O(log(log n))Correct answer is option 'D'. Can you explain this answer?.
Consider an interpolation search which is an improvement over binary search where the values in a sorted array are uniformly distributed. In interpolation search construction of new data points take place at different locations according to the value of the key being searched. Find the time complexity of interpolation search.a)O(log n)b)O(n)c)O(n log n)d)O(log(log n))Correct answer is option 'D'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Consider an interpolation search which is an improvement over binary search where the values in a sorted array are uniformly distributed. In interpolation search construction of new data points take place at different locations according to the value of the key being searched. Find the time complexity of interpolation search.a)O(log n)b)O(n)c)O(n log n)d)O(log(log n))Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider an interpolation search which is an improvement over binary search where the values in a sorted array are uniformly distributed. In interpolation search construction of new data points take place at different locations according to the value of the key being searched. Find the time complexity of interpolation search.a)O(log n)b)O(n)c)O(n log n)d)O(log(log n))Correct answer is option 'D'. Can you explain this answer?.
Solutions for Consider an interpolation search which is an improvement over binary search where the values in a sorted array are uniformly distributed. In interpolation search construction of new data points take place at different locations according to the value of the key being searched. Find the time complexity of interpolation search.a)O(log n)b)O(n)c)O(n log n)d)O(log(log n))Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Computer Science Engineering (CSE).
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Here you can find the meaning of Consider an interpolation search which is an improvement over binary search where the values in a sorted array are uniformly distributed. In interpolation search construction of new data points take place at different locations according to the value of the key being searched. Find the time complexity of interpolation search.a)O(log n)b)O(n)c)O(n log n)d)O(log(log n))Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider an interpolation search which is an improvement over binary search where the values in a sorted array are uniformly distributed. In interpolation search construction of new data points take place at different locations according to the value of the key being searched. Find the time complexity of interpolation search.a)O(log n)b)O(n)c)O(n log n)d)O(log(log n))Correct answer is option 'D'. Can you explain this answer?, a detailed solution for Consider an interpolation search which is an improvement over binary search where the values in a sorted array are uniformly distributed. In interpolation search construction of new data points take place at different locations according to the value of the key being searched. Find the time complexity of interpolation search.a)O(log n)b)O(n)c)O(n log n)d)O(log(log n))Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of Consider an interpolation search which is an improvement over binary search where the values in a sorted array are uniformly distributed. In interpolation search construction of new data points take place at different locations according to the value of the key being searched. Find the time complexity of interpolation search.a)O(log n)b)O(n)c)O(n log n)d)O(log(log n))Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider an interpolation search which is an improvement over binary search where the values in a sorted array are uniformly distributed. In interpolation search construction of new data points take place at different locations according to the value of the key being searched. Find the time complexity of interpolation search.a)O(log n)b)O(n)c)O(n log n)d)O(log(log n))Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice Computer Science Engineering (CSE) tests.
|
|
Explore Courses for Computer Science Engineering (CSE) exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup