Engineering Mathematics Exam > Engineering Mathematics Questions > Q Let P3 be the inner product space of polyno...
Start Learning for Free
Q Let P3 be the inner product space of polynomials of degree at most 3 over R with respect to the inner product f,g = lim1-0 integrate f(x)g(x)dx. Apply the Gram-Schmidt orthogonalisation process to find an orthonormal basis for the subspace of P3 generated by the vectors{1−2x,2x 6x^2,−3x^2 4x^3} .?
Verified Answer
Q Let P3 be the inner product space of polynomials of degree at most 3...
Ans.
Method to Solve :
Let v1 = 1
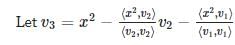
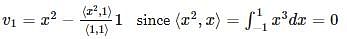
 This question is part of UPSC exam. View all Engineering Mathematics courses
This question is part of UPSC exam. View all Engineering Mathematics courses
Most Upvoted Answer
Q Let P3 be the inner product space of polynomials of degree at most 3...
Ans.
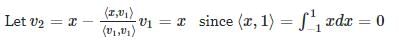
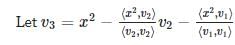
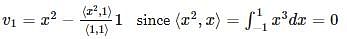
Method to Solve :
Let
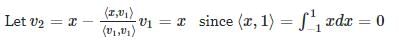
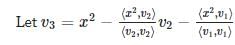
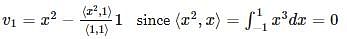
Community Answer
Q Let P3 be the inner product space of polynomials of degree at most 3...
Gram-Schmidt Orthogonalization Process
The Gram-Schmidt orthogonalization process is a method used to find an orthonormal basis for a given subspace of an inner product space. The process involves iteratively constructing orthogonal vectors and normalizing them to obtain an orthonormal basis.
Step 1: Finding the First Vector
To begin the process, we will find the first vector in the orthonormal basis. In this case, the given vectors are {1 - 2x, 2x, 6x^2, -3x^2 + 4x^3}. We can choose any non-zero vector from this set as the first vector. Let's choose the first vector as v1 = 1 - 2x.
Step 2: Orthogonalizing the Second Vector
Next, we need to orthogonalize the second vector, v2 = 2x, with respect to v1. We can do this by subtracting the projection of v2 onto v1 from v2. The projection of v2 onto v1 is given by:
proj(v2, v1) = (v2 · v1) / ||v1||^2 * v1
where · represents the inner product and ||v1|| is the norm of v1. In this case, the inner product is defined as f, g = lim1-0 integrate f(x)g(x)dx, and ||v1||^2 = (v1 · v1).
Calculating the projection, we have:
proj(v2, v1) = ((2x) · (1 - 2x)) / ((1 - 2x) · (1 - 2x)) * (1 - 2x)
= (2x - 4x^2) / (1 - 4x + 4x^2) * (1 - 2x)
= (2x - 4x^2) / (1 - 4x + 4x^2 - 2 + 4x)
= (2x - 4x^2) / (3 - 4x + 4x^2)
Subtracting the projection from v2, we get:
u2 = v2 - proj(v2, v1)
= 2x - (2x - 4x^2) / (3 - 4x + 4x^2)
Simplifying the expression, we have:
u2 = (6x^2 - 3x^2 + 4x^3) / (3 - 4x + 4x^2)
= (3x^2 + 4x^3) / (3 - 4x + 4x^2)
Step 3: Orthogonalizing the Third Vector
Now we need to orthogonalize the third vector, v3 = 6x^2, with respect to v1 and v2. Following the same procedure as before, we calculate the projection of v3 onto v1 and v2, and subtract them from v3.
proj(v3, v1) = ((6x^2) · (1 - 2x)) / ((1 - 2x) · (1 - 2x))
The Gram-Schmidt orthogonalization process is a method used to find an orthonormal basis for a given subspace of an inner product space. The process involves iteratively constructing orthogonal vectors and normalizing them to obtain an orthonormal basis.
Step 1: Finding the First Vector
To begin the process, we will find the first vector in the orthonormal basis. In this case, the given vectors are {1 - 2x, 2x, 6x^2, -3x^2 + 4x^3}. We can choose any non-zero vector from this set as the first vector. Let's choose the first vector as v1 = 1 - 2x.
Step 2: Orthogonalizing the Second Vector
Next, we need to orthogonalize the second vector, v2 = 2x, with respect to v1. We can do this by subtracting the projection of v2 onto v1 from v2. The projection of v2 onto v1 is given by:
proj(v2, v1) = (v2 · v1) / ||v1||^2 * v1
where · represents the inner product and ||v1|| is the norm of v1. In this case, the inner product is defined as f, g = lim1-0 integrate f(x)g(x)dx, and ||v1||^2 = (v1 · v1).
Calculating the projection, we have:
proj(v2, v1) = ((2x) · (1 - 2x)) / ((1 - 2x) · (1 - 2x)) * (1 - 2x)
= (2x - 4x^2) / (1 - 4x + 4x^2) * (1 - 2x)
= (2x - 4x^2) / (1 - 4x + 4x^2 - 2 + 4x)
= (2x - 4x^2) / (3 - 4x + 4x^2)
Subtracting the projection from v2, we get:
u2 = v2 - proj(v2, v1)
= 2x - (2x - 4x^2) / (3 - 4x + 4x^2)
Simplifying the expression, we have:
u2 = (6x^2 - 3x^2 + 4x^3) / (3 - 4x + 4x^2)
= (3x^2 + 4x^3) / (3 - 4x + 4x^2)
Step 3: Orthogonalizing the Third Vector
Now we need to orthogonalize the third vector, v3 = 6x^2, with respect to v1 and v2. Following the same procedure as before, we calculate the projection of v3 onto v1 and v2, and subtract them from v3.
proj(v3, v1) = ((6x^2) · (1 - 2x)) / ((1 - 2x) · (1 - 2x))

|
Explore Courses for Engineering Mathematics exam
|

|
Similar Engineering Mathematics Doubts
Q Let P3 be the inner product space of polynomials of degree at most 3 over R with respect to the inner product f,g = lim1-0 integrate f(x)g(x)dx. Apply the Gram-Schmidt orthogonalisation process to find an orthonormal basis for the subspace of P3 generated by the vectors{1−2x,2x 6x^2,−3x^2 4x^3} .?
Question Description
Q Let P3 be the inner product space of polynomials of degree at most 3 over R with respect to the inner product f,g = lim1-0 integrate f(x)g(x)dx. Apply the Gram-Schmidt orthogonalisation process to find an orthonormal basis for the subspace of P3 generated by the vectors{1−2x,2x 6x^2,−3x^2 4x^3} .? for Engineering Mathematics 2024 is part of Engineering Mathematics preparation. The Question and answers have been prepared according to the Engineering Mathematics exam syllabus. Information about Q Let P3 be the inner product space of polynomials of degree at most 3 over R with respect to the inner product f,g = lim1-0 integrate f(x)g(x)dx. Apply the Gram-Schmidt orthogonalisation process to find an orthonormal basis for the subspace of P3 generated by the vectors{1−2x,2x 6x^2,−3x^2 4x^3} .? covers all topics & solutions for Engineering Mathematics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Q Let P3 be the inner product space of polynomials of degree at most 3 over R with respect to the inner product f,g = lim1-0 integrate f(x)g(x)dx. Apply the Gram-Schmidt orthogonalisation process to find an orthonormal basis for the subspace of P3 generated by the vectors{1−2x,2x 6x^2,−3x^2 4x^3} .?.
Q Let P3 be the inner product space of polynomials of degree at most 3 over R with respect to the inner product f,g = lim1-0 integrate f(x)g(x)dx. Apply the Gram-Schmidt orthogonalisation process to find an orthonormal basis for the subspace of P3 generated by the vectors{1−2x,2x 6x^2,−3x^2 4x^3} .? for Engineering Mathematics 2024 is part of Engineering Mathematics preparation. The Question and answers have been prepared according to the Engineering Mathematics exam syllabus. Information about Q Let P3 be the inner product space of polynomials of degree at most 3 over R with respect to the inner product f,g = lim1-0 integrate f(x)g(x)dx. Apply the Gram-Schmidt orthogonalisation process to find an orthonormal basis for the subspace of P3 generated by the vectors{1−2x,2x 6x^2,−3x^2 4x^3} .? covers all topics & solutions for Engineering Mathematics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Q Let P3 be the inner product space of polynomials of degree at most 3 over R with respect to the inner product f,g = lim1-0 integrate f(x)g(x)dx. Apply the Gram-Schmidt orthogonalisation process to find an orthonormal basis for the subspace of P3 generated by the vectors{1−2x,2x 6x^2,−3x^2 4x^3} .?.
Solutions for Q Let P3 be the inner product space of polynomials of degree at most 3 over R with respect to the inner product f,g = lim1-0 integrate f(x)g(x)dx. Apply the Gram-Schmidt orthogonalisation process to find an orthonormal basis for the subspace of P3 generated by the vectors{1−2x,2x 6x^2,−3x^2 4x^3} .? in English & in Hindi are available as part of our courses for Engineering Mathematics .
Download more important topics, notes, lectures and mock test series for Engineering Mathematics Exam by signing up for free.
Here you can find the meaning of Q Let P3 be the inner product space of polynomials of degree at most 3 over R with respect to the inner product f,g = lim1-0 integrate f(x)g(x)dx. Apply the Gram-Schmidt orthogonalisation process to find an orthonormal basis for the subspace of P3 generated by the vectors{1−2x,2x 6x^2,−3x^2 4x^3} .? defined & explained in the simplest way possible. Besides giving the explanation of
Q Let P3 be the inner product space of polynomials of degree at most 3 over R with respect to the inner product f,g = lim1-0 integrate f(x)g(x)dx. Apply the Gram-Schmidt orthogonalisation process to find an orthonormal basis for the subspace of P3 generated by the vectors{1−2x,2x 6x^2,−3x^2 4x^3} .?, a detailed solution for Q Let P3 be the inner product space of polynomials of degree at most 3 over R with respect to the inner product f,g = lim1-0 integrate f(x)g(x)dx. Apply the Gram-Schmidt orthogonalisation process to find an orthonormal basis for the subspace of P3 generated by the vectors{1−2x,2x 6x^2,−3x^2 4x^3} .? has been provided alongside types of Q Let P3 be the inner product space of polynomials of degree at most 3 over R with respect to the inner product f,g = lim1-0 integrate f(x)g(x)dx. Apply the Gram-Schmidt orthogonalisation process to find an orthonormal basis for the subspace of P3 generated by the vectors{1−2x,2x 6x^2,−3x^2 4x^3} .? theory, EduRev gives you an
ample number of questions to practice Q Let P3 be the inner product space of polynomials of degree at most 3 over R with respect to the inner product f,g = lim1-0 integrate f(x)g(x)dx. Apply the Gram-Schmidt orthogonalisation process to find an orthonormal basis for the subspace of P3 generated by the vectors{1−2x,2x 6x^2,−3x^2 4x^3} .? tests, examples and also practice Engineering Mathematics tests.

|
Explore Courses for Engineering Mathematics exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















