Class 12 Exam > Class 12 Questions > How to derive lens makers formula?
Start Learning for Free
How to derive lens makers formula?
Verified Answer
How to derive lens makers formula?
Derivation Of Lens Maker Formula
Lenses of different focal lengths are used for various optical instruments. The focal length of a lens depends upon the refractive index of the material of the lens and the radii of curvatures of the two surfaces. The derivation of lens maker formula is provided here so that aspirants can understand the concept more effectively. The lens maker formula is commonly used by lens manufacturers for manufacturing lenses of desired focal length.
Lens Maker Formula Derivation
Lens Maker Formula Derivation
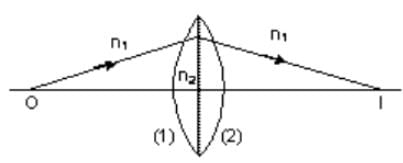
Assumptions
The following assumptions are taken for the derivation of lens maker formula.
Let us consider the thin lens shown in the image above with 2 refracting surfaces having the radii of curvatures R1 and R2 respectively.
Let the refractive indices of the surrounding medium and the lens material be n1 and n2 respectively.
Derivation
The complete derivation of lens maker formula is described below. Using the formula for refraction at a single spherical surface we can say that,
For the first surface,

Therefore we can say that,
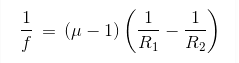
Where μ is the refractive index of the material.
This is the lens maker formula derivation. Check the limitations of the lens maker’s formula to understand the lens maker formula derivation is a better way.
Limitations of the lens maker’s formula
The lens should not be thick so that the space between the 2 refracting surfaces can be small.
The medium used on both sides of the lens should always be same.
 This question is part of UPSC exam. View all Class 12 courses
This question is part of UPSC exam. View all Class 12 courses
Most Upvoted Answer
How to derive lens makers formula?
Derivation of Lens Maker's Formula
To derive the lens maker's formula, let's consider a thin lens with two spherical surfaces. The lens has a refractive index of n and radii of curvature R1 and R2 for the first and second surfaces, respectively. The lens has a thickness of t at the center.
1. Lens Geometry
- The lens is assumed to be thin, meaning that its thickness is much smaller than the radii of curvature.
- The lens is symmetric, so the center of thickness coincides with the optical axis.
- The lens has an object at a distance u from the first surface and an image at a distance v from the second surface.
2. Refraction at the First Surface
- Using Snell's law, we can determine the angle of refraction at the first surface:
- n1 sin θ1 = n sin θ2
- θ1 is the angle of incidence, and θ2 is the angle of refraction.
- Since the lens is thin, we can assume small angles and approximate sin θ1 ≈ θ1 and sin θ2 ≈ θ2.
- Therefore, the lens equation for the first surface can be written as: θ1/n1 ≈ θ2/n
3. Refraction at the Second Surface
- Similarly, we can apply Snell's law to the second surface:
- n2 sin θ2 = n sin θ3
- θ3 is the angle of refraction after the light passes through the lens.
- By approximating sin θ2 ≈ θ2 and sin θ3 ≈ θ3, we get: θ2/n2 ≈ θ3/n
4. Lens Maker's Formula
- The lens equation relates the object distance (u), image distance (v), and the focal length (f) of the lens:
- 1/f = (n - 1) × (1/R1 - 1/R2)
- We can express the radii of curvature in terms of the lens geometry:
- R1 = R1 - t
- R2 = -R2 + t
- Plugging these values into the lens equation and simplifying, we obtain the lens maker's formula:
- 1/f = (n - 1) × [(n1 - 1)/R1 + (n2 - 1)/R2]
5. Sign Conventions
- The lens maker's formula considers the following sign conventions:
- Distances to the left of the lens are negative, and distances to the right are positive.
- Radii of curvature are positive for convex surfaces and negative for concave surfaces.
- Focal length is positive for converging lenses and negative for diverging lenses.
By applying these steps, the lens maker's formula can be derived, providing a useful tool for calculating the focal length of a lens based on its refractive index and geometry.

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
How to derive lens makers formula?
Question Description
How to derive lens makers formula? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about How to derive lens makers formula? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for How to derive lens makers formula?.
How to derive lens makers formula? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about How to derive lens makers formula? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for How to derive lens makers formula?.
Solutions for How to derive lens makers formula? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of How to derive lens makers formula? defined & explained in the simplest way possible. Besides giving the explanation of
How to derive lens makers formula?, a detailed solution for How to derive lens makers formula? has been provided alongside types of How to derive lens makers formula? theory, EduRev gives you an
ample number of questions to practice How to derive lens makers formula? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















