Class 11 Exam > Class 11 Questions > To which quadrants the interval belongs to( -...
Start Learning for Free
To which quadrants the interval belongs to( -pi/2,pi/2)?
Most Upvoted Answer
To which quadrants the interval belongs to( -pi/2,pi/2)?
Quadrants of the Interval (-π/2, π/2)
The interval (-π/2, π/2) refers to all real numbers that are greater than -π/2 and less than π/2. To determine which quadrants this interval belongs to, we must first understand the concept of quadrants and their corresponding angles.
Quadrants and Corresponding Angles
A quadrant is one of the four regions created by the intersection of the x-axis and the y-axis on a coordinate plane. Each quadrant is labeled with a Roman numeral I, II, III, or IV, starting from the top right and going counterclockwise. The angles in each quadrant have specific characteristics:
- Quadrant I: angles have a positive x-value and a positive y-value
- Quadrant II: angles have a negative x-value and a positive y-value
- Quadrant III: angles have a negative x-value and a negative y-value
- Quadrant IV: angles have a positive x-value and a negative y-value
For example, an angle of 45 degrees would be in quadrant I because it has a positive x and y value. An angle of 135 degrees would be in quadrant II because it has a negative x value and a positive y value.
Determining the Quadrants of (-π/2, π/2)
The interval (-π/2, π/2) contains all real numbers that are greater than -π/2 and less than π/2. We can convert these values to degrees to better understand which quadrants they belong to:
- -π/2 radians is equivalent to -90 degrees
- π/2 radians is equivalent to 90 degrees
Since the interval (-π/2, π/2) includes all real numbers between -90 and 90 degrees, we can conclude that it belongs to quadrants I and IV. This is because angles in quadrant I have a positive x and y value, which corresponds to angles between 0 and 90 degrees, and angles in quadrant IV have a positive x and negative y value, which corresponds to angles between 270 and 360 degrees.
Conclusion
The interval (-π/2, π/2) belongs to quadrants I and IV because it contains all real numbers between -90 and 90 degrees. Understanding the concept of quadrants and their corresponding angles is crucial in determining which quadrant a given angle or interval belongs to.
Community Answer
To which quadrants the interval belongs to( -pi/2,pi/2)?
|
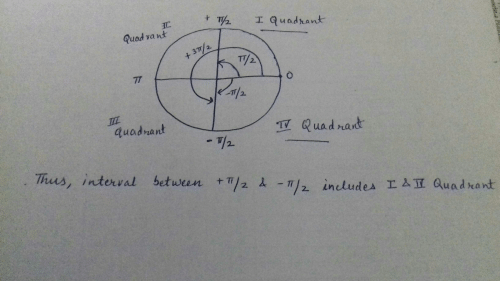
Explore Courses for Class 11 exam
|
|
Similar Class 11 Doubts
Top Courses for Class 11View all
To which quadrants the interval belongs to( -pi/2,pi/2)?
Question Description
To which quadrants the interval belongs to( -pi/2,pi/2)? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about To which quadrants the interval belongs to( -pi/2,pi/2)? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for To which quadrants the interval belongs to( -pi/2,pi/2)?.
To which quadrants the interval belongs to( -pi/2,pi/2)? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about To which quadrants the interval belongs to( -pi/2,pi/2)? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for To which quadrants the interval belongs to( -pi/2,pi/2)?.
Solutions for To which quadrants the interval belongs to( -pi/2,pi/2)? in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of To which quadrants the interval belongs to( -pi/2,pi/2)? defined & explained in the simplest way possible. Besides giving the explanation of
To which quadrants the interval belongs to( -pi/2,pi/2)?, a detailed solution for To which quadrants the interval belongs to( -pi/2,pi/2)? has been provided alongside types of To which quadrants the interval belongs to( -pi/2,pi/2)? theory, EduRev gives you an
ample number of questions to practice To which quadrants the interval belongs to( -pi/2,pi/2)? tests, examples and also practice Class 11 tests.
|
|
Explore Courses for Class 11 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup