Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > A rectangular block 6m long, 4m wide and 2m h...
Start Learning for Free
A rectangular block 6m long, 4m wide and 2m high is immersed in a oil of specific gravity 0.90. if the metacentric height for the stable equilibrium is 1.4m, then the depth of immersion of the rectangular block in a oil will be _____m.
(up to two decimal places)
Correct answer is '0.63-0.65'. Can you explain this answer?
Verified Answer
A rectangular block 6m long, 4m wide and 2m high is immersed in a oil ...
Concept:
Metacentric height of the rectangular block is given by:
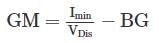
Imin = Moment of inertia of the plan about X – X or Y – Y (minimum value should be taken)
VDis = Volume of the displaced fluid
B G = Distance between centre of Buoyancy and centre of gravity of the block
Calculation:
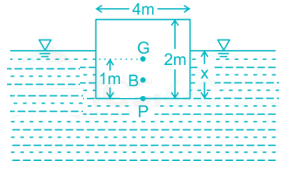
Let the Depth of immersion of the block will be ‘x’
GM = 1.4 m
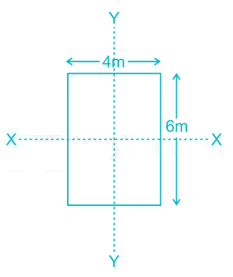
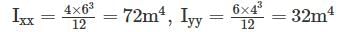
Imin = Iyy = 32 m4
BG = PG – PB

PG = 1 m

VDis = x × 4 × 6 = 24x
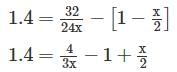

3x2 – 14.4x + 8 = 0
X1 = 4.16 m
X2 = 0.641 m
X1 = 4.16 m is not possible
So, X2 = x = 0.641 m
So, depth of immersion will be 0.641 m.
Most Upvoted Answer
A rectangular block 6m long, 4m wide and 2m high is immersed in a oil ...
Calculation of the Depth of Immersion of a Rectangular Block in Oil
Given data:
- Length of rectangular block (L) = 6m
- Width of rectangular block (B) = 4m
- Height of rectangular block (H) = 2m
- Specific gravity of oil (S) = 0.90
- Metacentric height (GM) = 1.4m
We need to find the depth of immersion (d) of the rectangular block in oil.
1. Determine the weight of the rectangular block
The weight of the rectangular block can be calculated using the formula:
Weight = Volume x Density x Gravity
- Volume (V) = L x B x H = 6m x 4m x 2m = 48m³
- Density (ρ) = 1,000 kg/m³ (density of water)
- Gravity (g) = 9.81 m/s²
Weight = 48m³ x 1,000 kg/m³ x 9.81 m/s² = 470,880 N
2. Determine the buoyant force acting on the block
The buoyant force acting on the block can be calculated using the formula:
Buoyant force = Volume displaced x Density of fluid x Gravity
- Volume displaced (Vd) = L x B x d
- Density of fluid (S) = 0.90 x 1,000 kg/m³ = 900 kg/m³
- Gravity (g) = 9.81 m/s²
Buoyant force = (L x B x d) x 900 kg/m³ x 9.81 m/s²
3. Determine the position of the center of gravity of the block
The center of gravity of the block can be assumed to be at the geometric center, which is at half of the height, i.e. at H/2 = 1m.
4. Determine the position of the metacenter
The metacenter is located at the intersection of the vertical line passing through the center of buoyancy and the line passing through the center of gravity of the block when it is tilted slightly. In this case, the block is rectangular and symmetrical, so the center of buoyancy coincides with the center of the block, which is at (L/2, B/2, d/2). Therefore, the metacenter is also at (L/2, B/2, GM+d/2).
5. Determine the righting moment
The righting moment is the product of the buoyant force and the distance between the metacenter and the center of gravity, which is (GM + d/2 - 1m).
Righting moment = Buoyant force x (GM + d/2 - 1m)
6. Find the equilibrium condition
For stable equilibrium, the righting moment must be greater than or equal to the overturning moment. The overturning moment is the product of the weight of the block and half of its height, which is 235,440 Nm.
Righting moment ≥ Overturning moment
Buoyant force x (GM + d/2 - 1m) ≥ 235,440 Nm
7. Solve for the depth of immersion
Substituting the values and solving for d, we get:
d ≥ 0.63m
Given data:
- Length of rectangular block (L) = 6m
- Width of rectangular block (B) = 4m
- Height of rectangular block (H) = 2m
- Specific gravity of oil (S) = 0.90
- Metacentric height (GM) = 1.4m
We need to find the depth of immersion (d) of the rectangular block in oil.
1. Determine the weight of the rectangular block
The weight of the rectangular block can be calculated using the formula:
Weight = Volume x Density x Gravity
- Volume (V) = L x B x H = 6m x 4m x 2m = 48m³
- Density (ρ) = 1,000 kg/m³ (density of water)
- Gravity (g) = 9.81 m/s²
Weight = 48m³ x 1,000 kg/m³ x 9.81 m/s² = 470,880 N
2. Determine the buoyant force acting on the block
The buoyant force acting on the block can be calculated using the formula:
Buoyant force = Volume displaced x Density of fluid x Gravity
- Volume displaced (Vd) = L x B x d
- Density of fluid (S) = 0.90 x 1,000 kg/m³ = 900 kg/m³
- Gravity (g) = 9.81 m/s²
Buoyant force = (L x B x d) x 900 kg/m³ x 9.81 m/s²
3. Determine the position of the center of gravity of the block
The center of gravity of the block can be assumed to be at the geometric center, which is at half of the height, i.e. at H/2 = 1m.
4. Determine the position of the metacenter
The metacenter is located at the intersection of the vertical line passing through the center of buoyancy and the line passing through the center of gravity of the block when it is tilted slightly. In this case, the block is rectangular and symmetrical, so the center of buoyancy coincides with the center of the block, which is at (L/2, B/2, d/2). Therefore, the metacenter is also at (L/2, B/2, GM+d/2).
5. Determine the righting moment
The righting moment is the product of the buoyant force and the distance between the metacenter and the center of gravity, which is (GM + d/2 - 1m).
Righting moment = Buoyant force x (GM + d/2 - 1m)
6. Find the equilibrium condition
For stable equilibrium, the righting moment must be greater than or equal to the overturning moment. The overturning moment is the product of the weight of the block and half of its height, which is 235,440 Nm.
Righting moment ≥ Overturning moment
Buoyant force x (GM + d/2 - 1m) ≥ 235,440 Nm
7. Solve for the depth of immersion
Substituting the values and solving for d, we get:
d ≥ 0.63m

|
Explore Courses for Civil Engineering (CE) exam
|

|
Similar Civil Engineering (CE) Doubts
A rectangular block 6m long, 4m wide and 2m high is immersed in a oil of specific gravity 0.90. if the metacentric height for the stable equilibrium is 1.4m, then the depth of immersion of the rectangular block in a oil will be _____m.(up to two decimal places)Correct answer is '0.63-0.65'. Can you explain this answer?
Question Description
A rectangular block 6m long, 4m wide and 2m high is immersed in a oil of specific gravity 0.90. if the metacentric height for the stable equilibrium is 1.4m, then the depth of immersion of the rectangular block in a oil will be _____m.(up to two decimal places)Correct answer is '0.63-0.65'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A rectangular block 6m long, 4m wide and 2m high is immersed in a oil of specific gravity 0.90. if the metacentric height for the stable equilibrium is 1.4m, then the depth of immersion of the rectangular block in a oil will be _____m.(up to two decimal places)Correct answer is '0.63-0.65'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A rectangular block 6m long, 4m wide and 2m high is immersed in a oil of specific gravity 0.90. if the metacentric height for the stable equilibrium is 1.4m, then the depth of immersion of the rectangular block in a oil will be _____m.(up to two decimal places)Correct answer is '0.63-0.65'. Can you explain this answer?.
A rectangular block 6m long, 4m wide and 2m high is immersed in a oil of specific gravity 0.90. if the metacentric height for the stable equilibrium is 1.4m, then the depth of immersion of the rectangular block in a oil will be _____m.(up to two decimal places)Correct answer is '0.63-0.65'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A rectangular block 6m long, 4m wide and 2m high is immersed in a oil of specific gravity 0.90. if the metacentric height for the stable equilibrium is 1.4m, then the depth of immersion of the rectangular block in a oil will be _____m.(up to two decimal places)Correct answer is '0.63-0.65'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A rectangular block 6m long, 4m wide and 2m high is immersed in a oil of specific gravity 0.90. if the metacentric height for the stable equilibrium is 1.4m, then the depth of immersion of the rectangular block in a oil will be _____m.(up to two decimal places)Correct answer is '0.63-0.65'. Can you explain this answer?.
Solutions for A rectangular block 6m long, 4m wide and 2m high is immersed in a oil of specific gravity 0.90. if the metacentric height for the stable equilibrium is 1.4m, then the depth of immersion of the rectangular block in a oil will be _____m.(up to two decimal places)Correct answer is '0.63-0.65'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of A rectangular block 6m long, 4m wide and 2m high is immersed in a oil of specific gravity 0.90. if the metacentric height for the stable equilibrium is 1.4m, then the depth of immersion of the rectangular block in a oil will be _____m.(up to two decimal places)Correct answer is '0.63-0.65'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A rectangular block 6m long, 4m wide and 2m high is immersed in a oil of specific gravity 0.90. if the metacentric height for the stable equilibrium is 1.4m, then the depth of immersion of the rectangular block in a oil will be _____m.(up to two decimal places)Correct answer is '0.63-0.65'. Can you explain this answer?, a detailed solution for A rectangular block 6m long, 4m wide and 2m high is immersed in a oil of specific gravity 0.90. if the metacentric height for the stable equilibrium is 1.4m, then the depth of immersion of the rectangular block in a oil will be _____m.(up to two decimal places)Correct answer is '0.63-0.65'. Can you explain this answer? has been provided alongside types of A rectangular block 6m long, 4m wide and 2m high is immersed in a oil of specific gravity 0.90. if the metacentric height for the stable equilibrium is 1.4m, then the depth of immersion of the rectangular block in a oil will be _____m.(up to two decimal places)Correct answer is '0.63-0.65'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A rectangular block 6m long, 4m wide and 2m high is immersed in a oil of specific gravity 0.90. if the metacentric height for the stable equilibrium is 1.4m, then the depth of immersion of the rectangular block in a oil will be _____m.(up to two decimal places)Correct answer is '0.63-0.65'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























