IIT JAM Exam > IIT JAM Questions > Two men are carrying a uniform bar of length ...
Start Learning for Free
Two men are carrying a uniform bar of length L on their shoulders. The bar is held horizontally such that younger man gets 1/4th of load. Suppose the younger man is at the end of the bar what is the distance of the other man from the end ?
Verified Answer
Two men are carrying a uniform bar of length L on their shoulders. The...
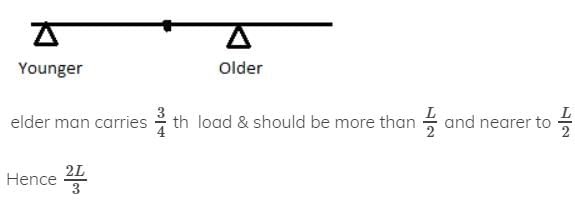
 This question is part of UPSC exam. View all IIT JAM courses
This question is part of UPSC exam. View all IIT JAM courses
Most Upvoted Answer
Two men are carrying a uniform bar of length L on their shoulders. The...
Understanding the Load Distribution
When two men are carrying a uniform bar, the load distribution depends on their positions and how much of the bar's weight each of them supports. In this scenario, the younger man at one end takes 1/4th of the load.
Load on Each Man
- The total weight of the bar can be represented as W.
- The younger man carries 1/4th of the load:
- Load on younger man = W/4
- Load on older man = W - W/4 = 3W/4
Finding the Distance from the End
To find the distance of the older man from the end of the bar where the younger man is positioned:
1. Set Up the System:
- Let the younger man be at point A (0 distance).
- Let the older man be at point B, which we need to determine.
2. Balance the Moments:
- The bar is uniform, so its center of mass is at L/2.
- For the system to be in equilibrium, the moments around any point must balance.
3. Calculate the Moment:
- Moment due to younger man: (W/4) * 0 = 0 (no distance to consider)
- Moment due to older man at distance x from the younger man: (3W/4) * (L - x)
4. Equilibrium Condition:
- Set the sum of moments around the center of mass:
(W/4) * (L/2) = (3W/4) * (L - x)
5. Solve for x:
- Simplifying gives:
x = (3L)/8
Conclusion
Thus, the distance of the older man from the end of the bar where the younger man is positioned is 3L/8. This indicates that the older man stands closer to the center of the bar, ensuring a balanced load distribution.
When two men are carrying a uniform bar, the load distribution depends on their positions and how much of the bar's weight each of them supports. In this scenario, the younger man at one end takes 1/4th of the load.
Load on Each Man
- The total weight of the bar can be represented as W.
- The younger man carries 1/4th of the load:
- Load on younger man = W/4
- Load on older man = W - W/4 = 3W/4
Finding the Distance from the End
To find the distance of the older man from the end of the bar where the younger man is positioned:
1. Set Up the System:
- Let the younger man be at point A (0 distance).
- Let the older man be at point B, which we need to determine.
2. Balance the Moments:
- The bar is uniform, so its center of mass is at L/2.
- For the system to be in equilibrium, the moments around any point must balance.
3. Calculate the Moment:
- Moment due to younger man: (W/4) * 0 = 0 (no distance to consider)
- Moment due to older man at distance x from the younger man: (3W/4) * (L - x)
4. Equilibrium Condition:
- Set the sum of moments around the center of mass:
(W/4) * (L/2) = (3W/4) * (L - x)
5. Solve for x:
- Simplifying gives:
x = (3L)/8
Conclusion
Thus, the distance of the older man from the end of the bar where the younger man is positioned is 3L/8. This indicates that the older man stands closer to the center of the bar, ensuring a balanced load distribution.

|
Explore Courses for IIT JAM exam
|

|
Similar IIT JAM Doubts
Two men are carrying a uniform bar of length L on their shoulders. The bar is held horizontally such that younger man gets 1/4th of load. Suppose the younger man is at the end of the bar what is the distance of the other man from the end ?
Question Description
Two men are carrying a uniform bar of length L on their shoulders. The bar is held horizontally such that younger man gets 1/4th of load. Suppose the younger man is at the end of the bar what is the distance of the other man from the end ? for IIT JAM 2024 is part of IIT JAM preparation. The Question and answers have been prepared according to the IIT JAM exam syllabus. Information about Two men are carrying a uniform bar of length L on their shoulders. The bar is held horizontally such that younger man gets 1/4th of load. Suppose the younger man is at the end of the bar what is the distance of the other man from the end ? covers all topics & solutions for IIT JAM 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two men are carrying a uniform bar of length L on their shoulders. The bar is held horizontally such that younger man gets 1/4th of load. Suppose the younger man is at the end of the bar what is the distance of the other man from the end ?.
Two men are carrying a uniform bar of length L on their shoulders. The bar is held horizontally such that younger man gets 1/4th of load. Suppose the younger man is at the end of the bar what is the distance of the other man from the end ? for IIT JAM 2024 is part of IIT JAM preparation. The Question and answers have been prepared according to the IIT JAM exam syllabus. Information about Two men are carrying a uniform bar of length L on their shoulders. The bar is held horizontally such that younger man gets 1/4th of load. Suppose the younger man is at the end of the bar what is the distance of the other man from the end ? covers all topics & solutions for IIT JAM 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two men are carrying a uniform bar of length L on their shoulders. The bar is held horizontally such that younger man gets 1/4th of load. Suppose the younger man is at the end of the bar what is the distance of the other man from the end ?.
Solutions for Two men are carrying a uniform bar of length L on their shoulders. The bar is held horizontally such that younger man gets 1/4th of load. Suppose the younger man is at the end of the bar what is the distance of the other man from the end ? in English & in Hindi are available as part of our courses for IIT JAM.
Download more important topics, notes, lectures and mock test series for IIT JAM Exam by signing up for free.
Here you can find the meaning of Two men are carrying a uniform bar of length L on their shoulders. The bar is held horizontally such that younger man gets 1/4th of load. Suppose the younger man is at the end of the bar what is the distance of the other man from the end ? defined & explained in the simplest way possible. Besides giving the explanation of
Two men are carrying a uniform bar of length L on their shoulders. The bar is held horizontally such that younger man gets 1/4th of load. Suppose the younger man is at the end of the bar what is the distance of the other man from the end ?, a detailed solution for Two men are carrying a uniform bar of length L on their shoulders. The bar is held horizontally such that younger man gets 1/4th of load. Suppose the younger man is at the end of the bar what is the distance of the other man from the end ? has been provided alongside types of Two men are carrying a uniform bar of length L on their shoulders. The bar is held horizontally such that younger man gets 1/4th of load. Suppose the younger man is at the end of the bar what is the distance of the other man from the end ? theory, EduRev gives you an
ample number of questions to practice Two men are carrying a uniform bar of length L on their shoulders. The bar is held horizontally such that younger man gets 1/4th of load. Suppose the younger man is at the end of the bar what is the distance of the other man from the end ? tests, examples and also practice IIT JAM tests.

|
Explore Courses for IIT JAM exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















