रेखाएँ और कोण Chapter Notes | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

परिचय

ज्यामिति की शुरुआत सबसे सरल अवधारणाओं से होती है: बिंदु, रेखाएँ, किरणें, रेखा खंड, और कोण। ये मौलिक विचार समतल ज्यामिति के निर्माण खंड हैं। इन्हें समझना आवश्यक है क्योंकि ये विभिन्न आकृतियों के निर्माण और विश्लेषण जैसे अधिक जटिल विषयों की खोज के लिए आधार प्रदान करते हैं।

बिंदु

कल्पना करें कि आप अपने कागज़ पर एक तेज़ पेंसिल से एक छोटा सा बिंदु बना रहे हैं। जितनी तेज़ नोक होगी, बिंदु उतना ही छोटा होगा। यह बिंदु आपको ज्यामिति में बिंदु का क्या अर्थ है, इसका एक विचार देता है। एक बिंदु एक सटीक स्थान को दर्शाता है, लेकिन इसका कोई आकार नहीं होता—न कोई लंबाई, चौड़ाई, या ऊँचाई—यह केवल एक स्थिति है।

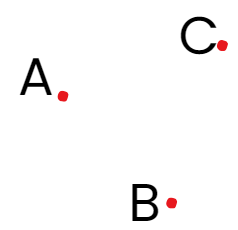
ज्यामिति में, हम बिंदुओं को बड़े अक्षरों से लेबल करते हैं जैसे A, B, या C। इन्हें "बिंदु A," "बिंदु B," और "बिंदु C" कहा जाता है। जबकि आप जो बिंदु देखते हैं, वे दृश्य होते हैं, ज्यामिति में ये सटीक स्थानों का प्रतिनिधित्व करते हैं, जिन्हें अत्यंत छोटे, लगभग अदृश्य माना जाता है।

रेखा खंड

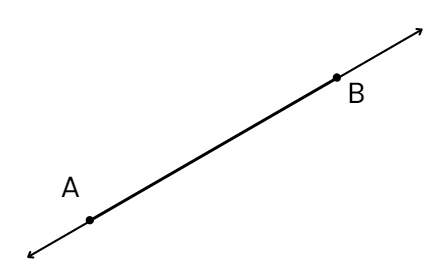
कल्पना करें कि आप एक कागज़ को मोड़ते हैं और फिर उसे खोलते हैं। आप देखेंगे कि जहां मोड़ किया गया था, वहाँ एक crease है। यह crease एक रेखा खंड के समान है। एक रेखा खंड के दो अंत बिंदु होते हैं, जिन्हें A और B के रूप में चिह्नित किया जा सकता है। इसे बेहतर समझने के लिए, एक कागज़ पर दो बिंदु, A और B, चिह्नित करें। A को B से जोड़ने के लिए विभिन्न मार्गों का प्रयास करें।

अब, सोचें कि कौन सा मार्ग सबसे छोटा है। A और B के बीच का सबसे छोटा मार्ग वही है जिसे हम रेखा खंड कहते हैं। यह रेखा खंड दोनों बिंदुओं A और B को शामिल करता है और इसे AB के रूप में लिखा जाता है। बिंदु A और B रेखा खंड के अंत बिंदु कहलाते हैं। खंड के प्रत्येक अंत पर स्थित बिंदुओं को अंत बिंदु कहा जाता है।

रेखा

रेखा एक रेखा खंड की तरह होती है लेकिन दोनों दिशाओं में अनंत विस्तार करती है। इसे इस तरह समझें कि A से B तक की रेखा खंड को दोनों दिशाओं में अनंत रूप से बढ़ाया जाए। यही विस्तारित रूप है जिसे हम रेखा कहते हैं। रेखा के कोई अंत बिंदु नहीं होते और यह दोनों दिशाओं में हमेशा के लिए चलती है। इसलिए आप कभी भी रेखा का एक पूरा चित्र नहीं बना सकते—यह अनंत होती है!

एक रेखा दोनों दिशाओं में हमेशा के लिए चलती है, जैसे एक अंतहीन सड़क। जबकि एक रेखा खंड उस सड़क का एक टुकड़ा होता है—इसके पास एक स्पष्ट प्रारंभ और अंत बिंदु होता है।

किरण

किरण एक रेखा की तरह होती है जो एक विशिष्ट बिंदु से शुरू होती है और एक दिशा में हमेशा के लिए चलती रहती है। जिस बिंदु से यह शुरू होती है, उसे प्रारंभ बिंदु या किरण का प्रारंभिक बिंदु कहा जाता है।

उदाहरण के लिए, एक टॉर्च से निकलने वाली रोशनी या एक लाइटहाउस की किरण एक किरण के समान होती है—यह स्रोत से शुरू होती है और चलती रहती है। हम एक किरण का प्रतिनिधित्व उसके प्रारंभ बिंदु और किरण पर एक अन्य बिंदु से करते हैं, जैसे कि किरण AB, जहाँ A प्रारंभ बिंदु है।

कोण

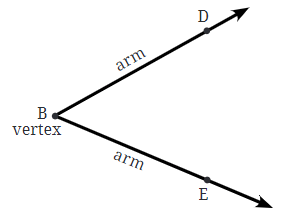
जब दो किरणें एक सामान्य प्रारंभ बिंदु साझा करती हैं, तो एक कोण बनता है। उदाहरण के लिए, यदि आपके पास किरणें हैं जो एक ही बिंदु B से शुरू होती हैं, तो वे एक कोण बनाती हैं। सामान्य बिंदु B को कोण का शीर्षक कहा जाता है, और किरणों को कोण के भुजाएँ कहा जाता है।

कोण का नामकरण

• कोण का नामकरण करने के लिए, आप बस शीर्षक का उपयोग कर सकते हैं, इसे "कोण B" कह सकते हैं।
• हालांकि, अधिक विशिष्ट होने के लिए, आप शीर्षक के साथ-साथ प्रत्येक भुजा से एक बिंदु का उपयोग करते हैं।
• उदाहरण के लिए, किरणों द्वारा बने कोण को कोण DBE या कोण EBD कहा जा सकता है।
• कोण का प्रतीक "∠" है, इसलिए आप इसे ∠DBE या ∠EBD के रूप में लिख सकते हैं। यह याद रखना महत्वपूर्ण है कि कोण का नामकरण करते समय शीर्षक (बिंदु B) हमेशा मध्य में लिखा जाता है।

कोणों के वास्तविक जीवन के उदाहरण

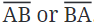
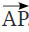
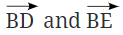
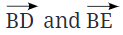
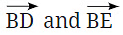
कोण हर जगह दैनिक जीवन में होते हैं:

• कंपास/डिवाइडर: जब आप कंपास की भुजाओं को घुमाते हैं, तो उनके मिलन बिंदु पर एक कोण बनता है।
• कैंची: जब आप कैंची के ब्लेड को खोलते हैं, तो वे एक कोण बनाते हैं, जहां वे मिलते हैं उसे शीर्ष बिंदु (vertex) कहा जाता है।

इन वस्तुओं को देखते हुए, आप देख सकते हैं कि कोण कैसे एक भाग के घूमने या मोड़ने से बनते हैं।

कोणों की तुलना करना

जब आप जानवरों के मुंह को खोलते हुए देखते हैं, तो आप वास्तव में उनके जबड़ों द्वारा बनते हुए कोण देख सकते हैं। कुछ मुंह दूसरों की तुलना में ज्यादा खोलते हैं, जिसका मतलब है कि उनके पास बड़े कोण होते हैं।

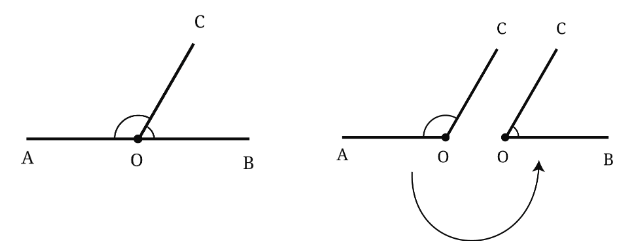
परत चढ़ाकर कोणों की तुलना

• दो कोणों की सटीक तुलना करने के लिए, आप एक कोण को दूसरे के ऊपर रख सकते हैं, जिसे परत चढ़ाना (superimposition) कहा जाता है। इसके लिए सुनिश्चित करें कि दोनों कोणों के शीर्ष बिंदु (vertices) एकदम मेल खाते हैं।
• परत चढ़ाने के बाद, यह देखना आसान हो जाता है कि कौन सा कोण छोटा है और कौन सा बड़ा है। उदाहरण के लिए, यदि आप ∠PQR को ∠ABC के ऊपर रखते हैं और भुजाएँ मेल नहीं खाती हैं, तो यह स्पष्ट होगा कि कौन सा कोण बड़ा है।

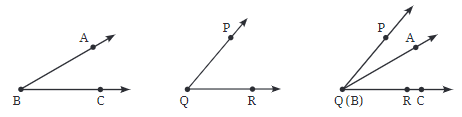
समान कोण

अब ∠AOB और ∠XOY जैसे कोणों पर विचार करें। आप कैसे बता सकते हैं कि वे समान आकार के हैं?

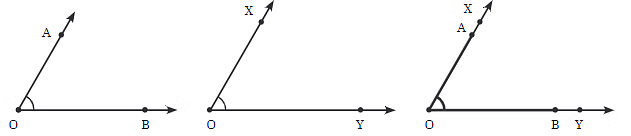
• जब आप दो कोणों की तुलना करते हैं, यदि उनके कोने (vertices) पूरी तरह से मेल खाते हैं और भुजाएँ (rays) एकदम ओवरलैप (overlap) होती हैं, जैसे OA का OX पर ओवरलैप होना और OB का OY पर ओवरलैप होना, तो यह दर्शाता है कि कोण आकार में समान हैं।
• इन कोणों को समान माना जाता है क्योंकि यदि आप प्रत्येक कोण को एक किरण (ray) को घुमाने के रूप में सोचते हैं, तो एक किरण को दूसरी पर लाने के लिए आवश्यक घुमाव की मात्रा दोनों कोणों के लिए समान होती है।
• परत चढ़ाने के दृष्टिकोण से, यदि दो कोणों को एक-दूसरे के ऊपर रखा जाता है, और उनके शीर्ष बिंदु और किरणें पूरी तरह से मेल खाती हैं, तो कोण आकार में समान होते हैं।

परत चढ़ाने के बिना कोणों की तुलना करना

यदि आप कोणों को सीधे सुपरइम्पोज़ नहीं करना चाहते हैं, तो क्या होगा? उदाहरण के लिए, दो क्रेन इस बारे में बहस कर रही हैं कि कौन अपना मुंह चौड़ा खोल सकता है। आप:

• एक पारदर्शी वृत्त का उपयोग करें: इसे एक कोण पर रखें ताकि वृत्त का केंद्र कोण के शिखर पर हो।
• वृत्त पर उन बिंदुओं को चिह्नित करें जहां कोण की भुजाएँ गुजरती हैं।
• वृत्त को दूसरे कोण पर ले जाएँ: शिखर को वृत्त के केंद्र के साथ संरेखित करें और देखें कि भुजाएँ वृत्त के माध्यम से कहाँ गुजरती हैं।

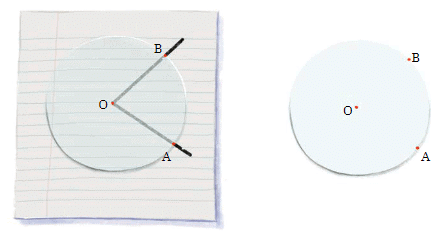
यह विधि आपको यह निर्धारित करने में मदद कर सकती है कि कौन सा कोण बड़ा है, बिना कोणों को भौतिक रूप से ओवरलैप किए। यह कोणों की तुलना करने का एक सुविधाजनक तरीका है, विशेषकर जब सुपरइम्पोज़ नहीं किया जा सकता।

घूर्णन भुजाएँ बनाना

आप कागज़ की स्ट्रॉ और एक पेपर क्लिप जैसी साधारण सामग्रियों का उपयोग करके घूर्णन भुजाएँ बना सकते हैं। इन चरणों का पालन करें:

• चरण 1: दो कागज़ की स्ट्रॉ और एक पेपर क्लिप लें।
• चरण 2: स्ट्रॉ को पेपर क्लिप के दो सिरों में डालें।
• चरण 3: आपकी घूर्णन भुजा तैयार है!

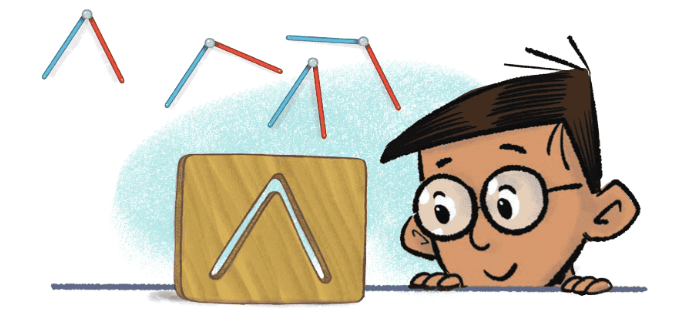
अब, स्ट्रॉ के बीच विभिन्न कोणों के साथ कई घूर्णन भुजाएँ बनाएं। जब आपने उन्हें बना लिया है, तो उन्हें एक-दूसरे के ऊपर रखकर (सुपरइम्पोज़ करके) कोणों की तुलना करें और उन्हें सबसे छोटे से बड़े तक व्यवस्थित करें।

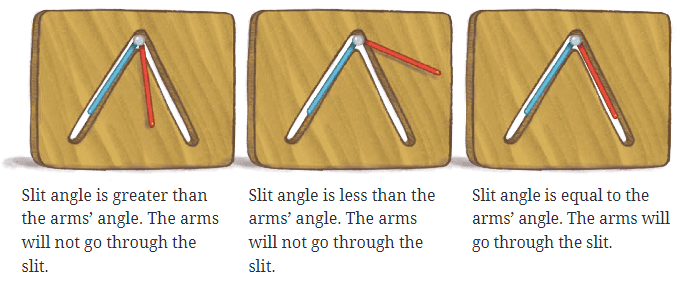
एक स्लिट के माध्यम से गुजरना

आइए, आपकी घूर्णन भुजाओं के साथ एक मजेदार गतिविधि करें। पहले, विभिन्न कोणों के साथ कई घूर्णन भुजाएँ इकट्ठा करें, लेकिन गतिविधि के दौरान उन्हें घुमाएँ नहीं। एक कार्डबोर्ड का टुकड़ा लें और अपने घूर्णन भुजा के एक आकार के अनुसार एक स्लिट बनाएं। अब, अपनी सभी घूर्णन भुजाओं को शफल और मिश्रित करें। आपका कार्य यह पता लगाना है कि कौन सी घूर्णन भुजा स्लिट के माध्यम से गुज़र सकती है। इसके लिए, प्रत्येक घूर्णन भुजा को स्लिट के ऊपर रखें और देखें कि क्या यह फिट होती है। केवल वही घूर्णन भुजा जो स्लिट के कोण से मेल खाती है, वह इसके माध्यम से गुज़रेगी। याद रखें, भुजा का स्लिट में फिट होना कोण पर निर्भर करता है, न कि भुजाओं की लंबाई पर (जब तक वे स्लिट से छोटी हैं)।

विशेष प्रकार के कोण
आइए कुछ विशेष प्रकार के कोणों का अन्वेषण करें, एक अलग उदाहरण के साथ।

सपाट कोण और समकोण

अब, इस सपाट कोण के बारे में सोचें, ∠AOB, जहाँ A और B दरवाज़े और दीवार पर बिंदु हैं, और O काज है। यदि आप काज (O) से दरवाज़े के किनारे (C) तक एक धागा लगाते हैं, तो यह धागा सपाट कोण को दो छोटे कोणों, ∠AOC और ∠COB में विभाजित करेगा।

प्रश्न है: क्या आप धागा ऐसे रख सकते हैं कि ये दोनों कोण समान हों?

यहाँ जानने का तरीका है:

• कागज मोड़ना: कल्पना करें कि आपके पास एक कागज़ है जिसे आप आधा मोड़ते हैं। यह मोड़ एक रेखा का प्रतिनिधित्व करता है जो एक सपाट कोण को दो समान भागों में विभाजित करता है।
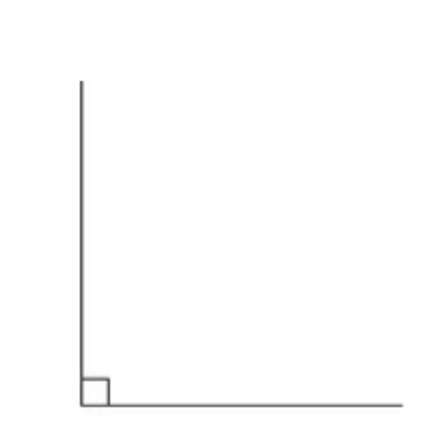
• समकोण: बने हुए दो समान कोणों को समकोण कहा जाता है। एक सपाट कोण में दो समकोण होते हैं। जब दरवाज़ा दीवार के साथ समकोण बनाने के लिए खोला जाता है, तो यह 'L' के आकार का दिखता है। यह एक सपाट कोण का आधा है।
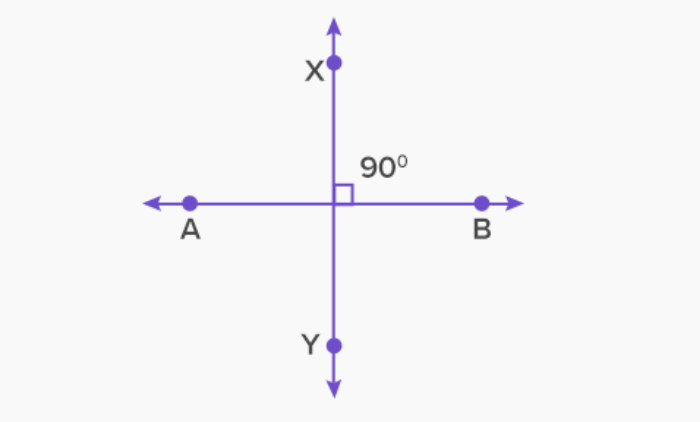
• लंबवत रेखाएँ: यदि आप छत से फर्श तक एक धागा लंबवत लगाते हैं, तो यह फर्श के साथ समकोण बनाएगा, जिससे दोनों रेखाएँ लंबवत बनेंगी।

कोणों का वर्गीकरण

कोणों को तीन मुख्य समूहों में वर्गीकृत किया जा सकता है:

• तीव्र कोण: ये कोण सीधे कोण से कम होते हैं। ये तेज और संकीर्ण होते हैं, जैसे जब दरवाजा थोड़ा खुला होता है।

• सही कोण: ये बिल्कुल सीधे कोण के बराबर होते हैं। जब दरवाजा आधा खुला होता है, तो यह फर्श के साथ एक सही 'एल' आकार बनाता है।

• obtuse कोण: ये कोण सीधे कोण से बड़े होते हैं लेकिन सीधे कोण से छोटे होते हैं। ये तब बनते हैं जब दरवाजा और अधिक खुला होता है लेकिन दीवार के साथ पूरी तरह से सीध में नहीं होता। दरवाजे का यह उदाहरण विभिन्न प्रकार के कोणों को समझने में मदद करता है और यह कैसे खुलते या घुमते हैं, के आधार पर वर्गीकृत होते हैं।

• सीधा कोण: यह एक कोण है जो ठीक 180° के बराबर होता है। यह एक सीधी रेखा जैसा दिखता है। उदाहरण के लिए, कागज़ के एक टुकड़े के कोने सही कोण होते हैं, और कैंची के थोड़े खुले होने पर बनने वाले कोण तीव्र कोण होते हैं।

कोणों का मापन

कोणों को सटीक रूप से मापने के लिए, गणितज्ञों ने वृत्त को 360 समान भागों में विभाजित किया। प्रत्येक भाग 1 डिग्री का प्रतिनिधित्व करता है, जिसे 1° के रूप में लिखा जाता है। विचार यह है कि एक कोण का माप बस उन 1° इकाइयों की संख्या है जो उसमें फिट होती हैं। उदाहरण के लिए:

कोणों के माप

• पूर्ण चक्र: एक पूर्ण वृत्त में 360° होते हैं। इसलिए, एक पूर्ण चक्र 360° होता है।
• सीधा कोण: एक सीधा कोण पूर्ण चक्र का आधा होता है। चूंकि पूर्ण चक्र 360° है, इसलिए एक सीधा कोण 180° होता है।
• दाहिना कोण: दो दाहिने कोण मिलकर एक सीधा कोण बनाते हैं। चूंकि एक सीधा कोण 180° है, इसलिए एक दाहिना कोण 90° होता है।

उदाहरण के लिए, यदि आप घड़ी की सुइयों को देखें, तो विभिन्न समय पर उनके बीच का कोण डिग्री में मापा जा सकता है। 3 बजे, घंटे और मिनट की सुइयों के बीच का कोण एक दाहिना कोण (90°) होता है।

360 डिग्री क्यों?

लेकिन 360° क्यों? इसका सही कारण थोड़ा सा रहस्य है, लेकिन कई ऐतिहासिक कारण हैं:

• प्राचीन सभ्यताएँ, जैसे कि भारत, फारस, बाबुल, और मिस्र ने अपने कैलेंडरों में 360 दिनों वाला वर्ष उपयोग किया।
• संख्याएँ 360 व्यावहारिक हैं क्योंकि इसे कई संख्याओं (जैसे 1, 2, 3, 4, 5, 6, 8, 9, 10, और 12) द्वारा समान रूप से विभाजित किया जा सकता है, जिससे वृत्त को समान भागों में विभाजित करना आसान हो जाता है।

यह विभाज्यता ही कारण है कि 360° का उपयोग इतने लंबे समय से किया जा रहा है—यह वास्तव में सुविधाजनक है!

कोणों के डिग्री माप

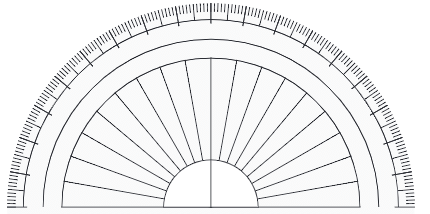
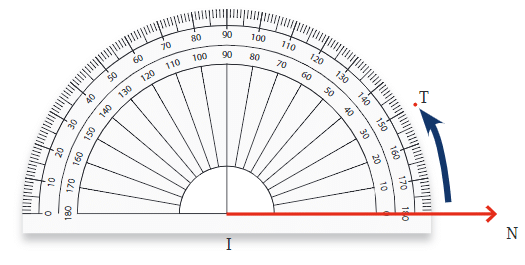
कोणों को मापना ज्यामिति का एक मौलिक सिद्धांत है, और इसे सटीकता से करने के लिए हम एक उपकरण का उपयोग करते हैं जिसे प्रोट्रैक्टर कहा जाता है। एक प्रोट्रैक्टर या तो एक पूर्ण वृत्त होता है जिसे 360 समान भागों में विभाजित किया गया है या एक आधा वृत्त जिसे 180 समान भागों में विभाजित किया गया है।

प्रोट्रैक्टर का उपयोग करना

• प्रोट्रैक्टर की संरचना: एक सामान्य प्रोट्रैक्टर के केंद्र में एक सीधा कोण होता है, जिसे 180 इकाइयों में विभाजित किया गया है, प्रत्येक 1 डिग्री के बराबर। ये इकाइयाँ आपको कोणों को सटीक रूप से मापने में मदद करती हैं।
• प्रोट्रैक्टर को पढ़ना: सबसे दाहिने बिंदु से शुरू करते हुए, हर 10 डिग्री के लिए लंबे मार्क और हर 5 डिग्री के लिए मध्यम आकार के मार्क होते हैं। इससे कोणों को गिनना और मापना आसान हो जाता है।

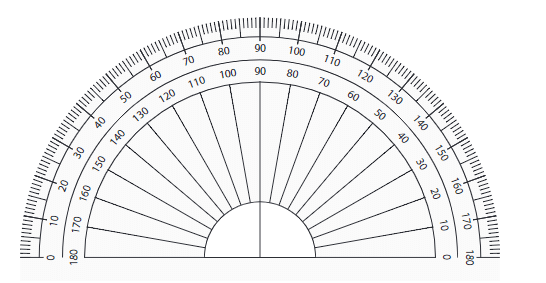
प्रोट्रैक्टर के दो प्रकार होते हैं:

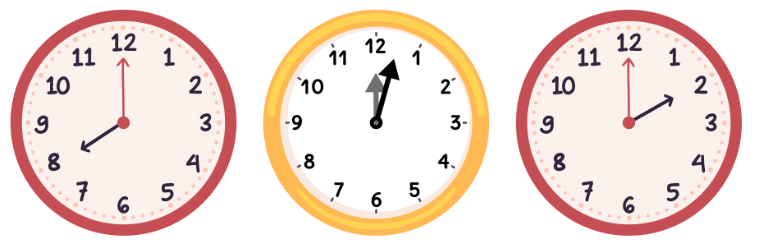
अंकगणित में कोणों को मापने के लिए प्रोट्रैक्टर का उपयोग किया जाता है। प्रोट्रैक्टर दो प्रकार के होते हैं:

• अनलेबल्ड प्रोट्रैक्टर: यह एक प्रोट्रैक्टर है जिसमें संख्या नहीं होती, केवल मार्किंग होती है। कोण को मापने के लिए आपको मार्किंग से डिग्री यूनिट्स को गिनना होता है। इसके लिए आपको हर छोटी मार्क को ध्यान से गिनना होता है।
• लेबल्ड प्रोट्रैक्टर: यह एक प्रोट्रैक्टर है जिसमें संख्या होती है, जिससे कोणों को मापना आसान होता है। संख्या आमतौर पर 0° से 180° तक होती है, दोनों दिशाओं में (घड़ी की दिशा में और घड़ी की दिशा के विपरीत)। लेबल्ड प्रोट्रैक्टर का उपयोग करने से कोणों को मापने की प्रक्रिया सरल हो जाती है, क्योंकि आप सीधे कोण के डिग्री माप को देख सकते हैं।

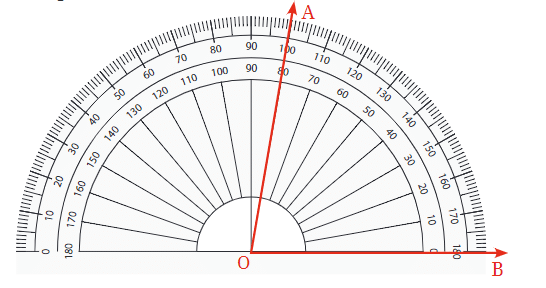
कोण मापने की प्रक्रिया:

• प्रोट्रैक्टर रखें: प्रोट्रैक्टर को इस तरह संरेखित करें कि इसका केंद्र कोण के शीर्ष पर हो।
• एक भुजा को संरेखित करें: सुनिश्चित करें कि कोण की एक भुजा प्रोट्रैक्टर पर 0° मार्क से होकर गुजरती है।
• माप पढ़ें: प्रोट्रैक्टर पर वह संख्या जहाँ दूसरी भुजा गुजरती है, वह कोण का माप डिग्री में दर्शाती है।

अपना खुद का प्रोट्रैक्टर बनाना:

आप कागज का उपयोग करके एक साधारण प्रोट्रैक्टर बना सकते हैं:

चक्र बनाना: सबसे पहले एक कागज़ पर एक चक्र (Circle) बनाएं और उसे काट लें।

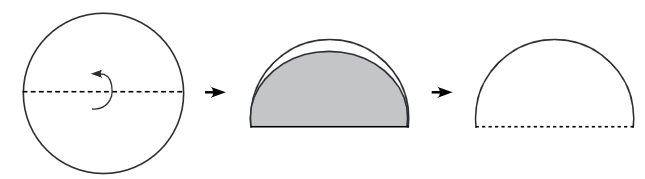
आर्ध चक्र बनाना: चक्र को आधा मोड़ें ताकि एक आर्ध चक्र (Semicircle) बन जाए। दाईं ओर कोने को 0° और बाईं ओर कोने को 180° चिह्नित करें।

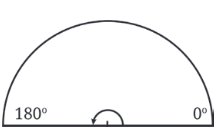
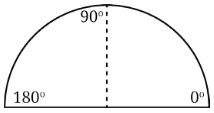
चौथाई चक्र बनाना: आर्ध चक्र को फिर से मोड़ें ताकि एक चौथाई चक्र (Quarter Circle) बन जाए। अब आर्ध चक्र का शीर्ष 90° को दर्शाता है।

अधिक विभाजन: छोटे कोण जैसे 45°, 135° आदि बनाने के लिए मोड़ना जारी रखें। प्रत्येक नया मोड़ कोण को बाईसेक्ट (Bisects) करता है, जिससे आपको सटीक माप मिलती है।

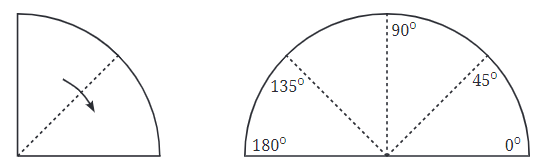
प्रत्येक बार जब आप कागज़ को मोड़ते हैं, तो आप कोण को बाईसेक्ट कर रहे हैं, जिसका अर्थ है आप कोण को दो समान भागों में विभाजित कर रहे हैं। मोड़ से बनी रेखा को कोण बाईसेक्टर (Angle Bisector) कहा जाता है।

गलतियों पर ध्यान दें, उन्हें सुधारें!

प्रो्ट्रैक्टर (Protractor) का उपयोग करते समय, गलतियाँ करना आसान है। यहां कुछ सामान्य गलतियाँ और उन्हें कैसे ठीक करें:

• गलत स्थान: गलती: प्रो्ट्रैक्टर का केंद्र बिंदु शीर्ष पर नहीं है।
  सुधार: सुनिश्चित करें कि प्रो्ट्रैक्टर का केंद्र बिंदु बिल्कुल शीर्ष पर है।

• असंगति: गलती: कोण की आधार रेखा 0° रेखा के साथ संरेखित नहीं है।
  सुधार: कोण की एक भुजा को प्रो्ट्रैक्टर पर 0° रेखा के साथ संरेखित करें।

• गलत स्केल: गलती: गलत स्केल (आंतरिक बनाम बाह्य) पढ़ना।
  सुधार: प्रो्ट्रैक्टर की संरेखण के आधार पर सही स्केल का उपयोग करें।

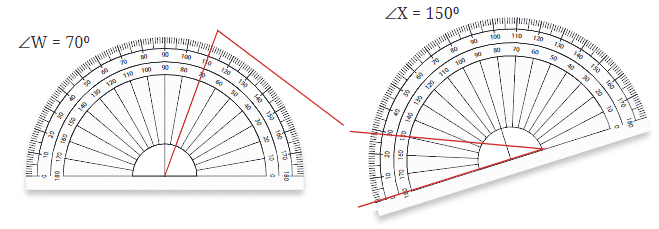
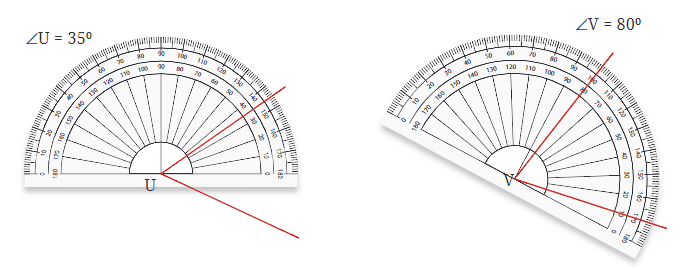
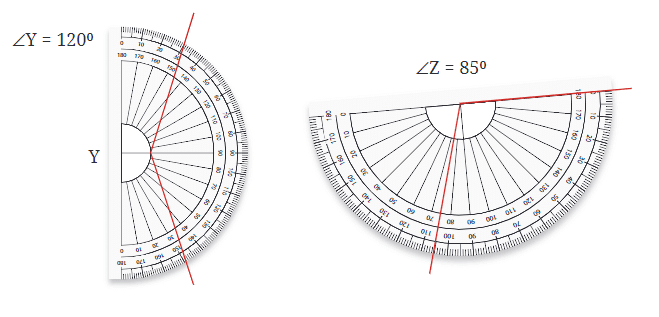
कोण बनाना

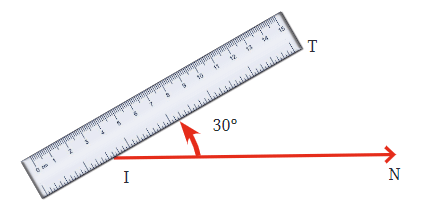
∠AOB को प्रो्ट्रैक्टर का उपयोग करके मापने के लिए: एक विशिष्ट डिग्री माप के साथ कोण बनाने के लिए, आप प्रो्ट्रैक्टर का उपयोग कर सकते हैं। उदाहरण के लिए, 30° कोण बनाने के लिए:

• एक सीधी रेखा खींचें, जो कोण की एक भुजा होगी।

• प्रो्ट्रैक्टर का केंद्र रेखा के एक छोर पर रखें।

• प्रो्ट्रैक्टर के आधार को रेखा के साथ संरेखित करें।
• प्रो्ट्रैक्टर पर 30° का चिह्न खोजें और कागज़ पर एक छोटा चिह्न बनाएं।

• प्रो्ट्रैक्टर को हटा दें और मूल रेखा के अंत से चिह्न तक एक रेखा खींचें। यह रेखा कोण की दूसरी भुजा बनाती है, जिससे 30° कोण बनता है।

• यह प्रक्रिया आपको सटीक कोण बनाने में मदद करती है, जिसका उपयोग ज्यामिति और अन्य गणितीय अनुप्रयोगों में किया जा सकता है।

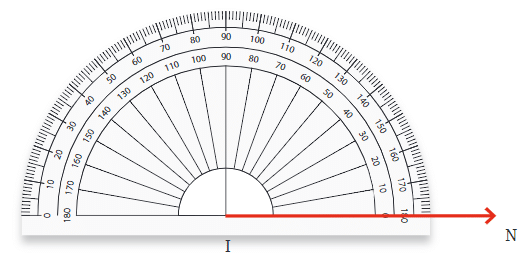
कोणों के प्रकार और उनके माप

हमने विभिन्न प्रकार के कोणों का अन्वेषण किया है, जिसमें सीधा और समकोण शामिल हैं। चलिए देखते हैं कि अन्य कोणों को कैसे मापा जाता है:

• तीव्र कोण: एक तीव्र कोण समकोण से छोटा होता है, यानी इसका माप 90° से कम लेकिन 0° से अधिक होता है। उदाहरण: 40° का कोण एक तीव्र कोण है।

• उदाहरण: 40° का कोण एक तीव्र कोण है।

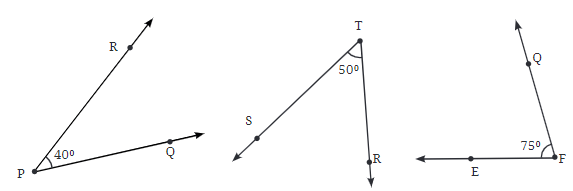
• अधूरा कोण: एक अधूरा कोण समकोण से बड़ा लेकिन सीधा कोण से छोटा होता है, इसलिए इसका माप 90° से अधिक लेकिन 180° से कम होता है। उदाहरण: 130° का कोण एक अधूरा कोण है।

• उदाहरण: 130° का कोण एक अधूरा कोण है।

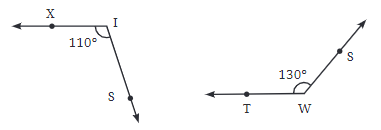
• प्रतिवर्तन कोण: एक प्रतिवर्तन कोण सीधा कोण से बड़ा होता है लेकिन पूरा वृत्त से छोटा होता है। इसका माप 180° से अधिक लेकिन 360° से कम होता है।

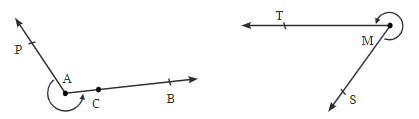
ये प्रकार सभी संभावित कोणों को उनके डिग्री माप के आधार पर कवर करते हैं।

मुख्य बिंदु:

• एक बिंदु एक स्थान है जिसका आकार नहीं होता, इसे एक बिंदु द्वारा दर्शाया जाता है और इसे एक बड़े अक्षर जैसे A, B, या C से लेबल किया जाता है।
• एक रेखा खंड दो बिंदुओं के बीच की सबसे छोटी दूरी है, जिसके दो अंत बिंदु होते हैं, और इसे AB या BA के रूप में दर्शाया जाता है।
• एक रेखा अनंत रूप से दोनों दिशाओं में बढ़ती है, इसके अंत बिंदु नहीं होते हैं, और इसे दो बिंदुओं या एक छोटे अक्षर द्वारा दर्शाया जा सकता है।
• एक किरण एक बिंदु से शुरू होती है और एक दिशा में अनंत तक बढ़ती है, इसे प्रारंभ बिंदु और किरण पर एक अन्य बिंदु द्वारा दर्शाया जाता है, जैसे कि किरण AB।
• एक कोण दो किरणों द्वारा बनाया जाता है जो एक सामान्य प्रारंभ बिंदु को साझा करते हैं जिसे शीर्षक कहा जाता है, और इसे एक किरण से दूसरी किरण के घूमने से मापा जाता है।
• कोणों को डिग्री (°) में मापा जाता है, एक पूरा वृत्त 360°, एक सीधा कोण 180°, और एक समकोण 90° होता है।
• एक प्रोट्रैक्टर एक उपकरण है जिसका उपयोग कोणों को मापने के लिए किया जाता है, लेबल वाले प्रोट्रैक्टर्स में आसान पढ़ाई के लिए चिह्नित डिग्री होती हैं, जबकि बिना लेबल वाले प्रोट्रैक्टर्स में डिग्री इकाइयों की सावधानीपूर्वक गिनती की आवश्यकता होती है।
• एक कोण द्विभाजक एक रेखा या किरण होती है जो एक कोण को दो समान भागों में विभाजित करती है, जिससे दो समान माप के कोण बनते हैं।
• कोणों को तीव्र (90° से कम), सम (सटीक 90°), अधूरा (90° से अधिक लेकिन 180° से कम), सीधा (180°), और प्रतिवर्तन (180° से अधिक लेकिन 360° से कम) के रूप में वर्गीकृत किया जाता है।

चलो अभ्यास करते हैं!

प्रश्न 1. दो कोणों के रफ चित्र बनाएँ ताकि उनके बीच निम्नलिखित समानताएँ हों:

• (क) एक बिंदु सामान्य हो।
• (ख) दो बिंदु सामान्य हों।

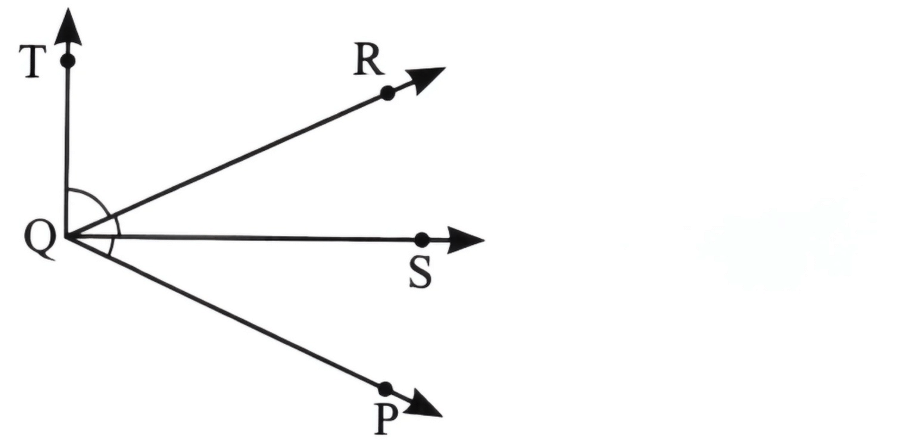
उत्तर: (क) नीचे दिए गए चित्र में, ∠PQS और ∠RQT का एक बिंदु Q सामान्य है।

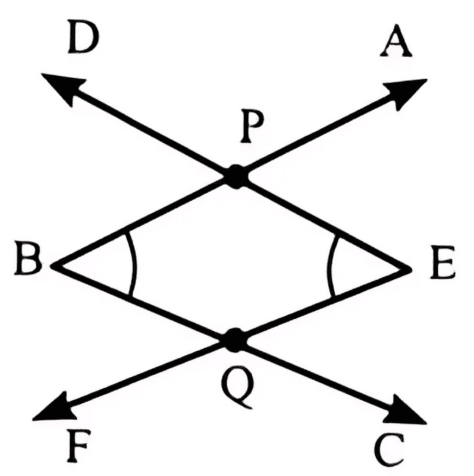
(ख) नीचे दिए गए चित्र में, ∠ABC और ∠DEF के दो बिंदु P और Q सामान्य हैं।