अवलोकन: एकात्मक विधि | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
एकात्मक विधि
एकात्मक विधि की परिभाषा: एकात्मक विधि एक गणितीय प्रक्रिया है जिसका उपयोग एकल इकाई के मूल्य को कई इकाइयों के मूल्य से और कई इकाई दर के मूल्य को एकल इकाई के मूल्य से निकालने के लिए किया जाता है।
- यह एक संख्यात्मक प्रक्रिया है जिसका उपयोग हम किसी भी मूल्य जैसे कि लागत, गति या किसी भी आवश्यक मात्रा की गणना करने के लिए करते हैं।
- इस विधि का प्राथमिक शर्त यह है कि हमें कुछ मात्रा के मूल्य प्रदान किए जाने चाहिए, और फिर हम एकात्मक विधि का उपयोग करके आवश्यक मात्रा का मूल्य निकाल सकते हैं।
उदाहरण 1: यदि हमें डेटा प्रदान किया गया है जहाँ कहा गया है कि 3 छात्र मिलकर एक समूह परियोजना को 5 घंटे में पूरा कर सकते हैं, और हमें यह गणना करनी है कि यदि समूह में 5 छात्र हैं, तो उस परियोजना को पूरा करने में कितने घंटे लगेंगे। हल: यहाँ हमारे पास एक निश्चित मात्रा का मूल्य है, अर्थात् 3 छात्रों को पूरा करने के लिए 5 घंटे की आवश्यकता है, और हमें आवश्यक मात्रा का मूल्य निकालना है, अर्थात् 5 छात्रों द्वारा आवश्यक घंटे। इसलिए, हम यहाँ एकात्मक विधि का उपयोग कर सकते हैं। एक छात्र द्वारा लिए गए घंटे = 5/3 = 1.6667। इसलिए, 5 छात्रों द्वारा लिए गए घंटे = 1.6667 × 5 = 8.3335।
एकात्मक विधि के प्रकार
एकात्मक विधि का उपयोग करते समय हम दो प्रकार की परिवर्तनशीलता देखते हैं।
प्रत्यक्ष परिवर्तन
- यह दी गई मात्रा के मूल्य और आवश्यक मात्रा के मूल्य के बीच एक प्रत्यक्ष संबंध है। अन्य शब्दों में, यदि एक मात्रा का मूल्य बढ़ता है, तो दूसरी मात्रा का मूल्य भी बढ़ता है और इसके विपरीत। हम यह भी कह सकते हैं कि एक मूल्य दूसरे मूल्य के सीधे अनुपात में है। उदाहरण के लिए, यदि एक कार की गति बढ़ती है, तो दूरी भी बढ़ती है और इसी प्रकार, यदि एक कार की गति घटती है, तो दूरी भी घटती है। यह गति, समय और दूरी के बीच प्रत्यक्ष परिवर्तन को दर्शाता है।
अप्रत्यक्ष परिवर्तन
यह एक अप्रत्यक्ष सीधा संबंध है जो दी गई मात्रा के मूल्य और आवश्यक मात्रा के मूल्य के बीच होता है। दूसरे शब्दों में, यदि एक मात्रा का मूल्य बढ़ता है, तो दूसरी मात्रा का मूल्य घटता है और इसके विपरीत। हम यह भी कह सकते हैं कि एक मूल्य दूसरे मूल्य के विपरीत आनुपातिक है। उदाहरण के लिए, जब एक कार की गति बढ़ती है, तो दूरी को कवर करने में लगने वाला समय कम होता है, जबकि जब कार की गति घटती है, तो उसी दूरी को कवर करने में लगने वाला समय बढ़ता है। यह गति और समय के बीच अप्रत्यक्ष परिवर्तन को दर्शाता है।
यूनिटरी विधि का उपयोग करने के चरण
यूनिटरी विधि का उपयोग करने के चरण नीचे उल्लेखित हैं।
- चरण 1: सबसे पहले, हम दी गई मात्रा को दी गई मूल्य से विभाजित करके इकाई मात्रा का मूल्य निकालते हैं। इस प्रकार, हम इकाई मात्रा का मूल्य प्राप्त करते हैं।
- चरण 2: फिर हम आवश्यक मात्रा को प्राप्त मूल्य के साथ गुणा करते हैं। इसलिए हमें आवश्यक मात्रा का मूल्य मिलता है।
उदाहरण 2: हमें 10 गेंदों की खरीद की लागत दी गई है, जो कि 95 रुपये है, और हमें 7 गेंदों की लागत निकालनी है। समाधान: ऊपर उल्लिखित चरण 1 के अनुसार, हम सबसे पहले इकाई मात्रा का मूल्य निकालते हैं, अर्थात् एक गेंद की खरीद की लागत = 95/10 = 9.5 रुपये। अब हम चरण 2 में उल्लेखित आवश्यक मात्रा का मूल्य निकाल सकते हैं, अर्थात् 1 गेंद की लागत को प्राप्त मूल्य के साथ गुणा करके, यानी 9.5 x 7 = 68.5 रुपये। इस प्रकार, हमें यूनिटरी विधि का उपयोग करके 7 गेंदों की लागत मिलती है, जो कि 68.5 रुपये है।
अनुपात और अनुपात में एकात्मक विधि
एकात्मक विधि का उपयोग एक मात्रा के अनुपात को दूसरी मात्रा के सापेक्ष खोजने के लिए किया जाता है। अनुपात-प्रपोर्शन और एकात्मक विधि की अवधारणाएँ एक-दूसरे से बहुत अधिक संबंधित हैं। अनुपात और अनुपात के व्यायाम के योग भिन्नों पर आधारित होते हैं। एक भिन्न को a:b के रूप में दर्शाया जाता है। a और b कोई भी दो पूर्णांक हो सकते हैं।
उदाहरण 3: हरिश की मासिक आय Rs 20000 है, और शालिनी की वार्षिक आय Rs 191520 है। यदि प्रत्येक का मासिक व्यय Rs 9000 है, तो उनके बचत का अनुपात ज्ञात करें। समाधान:
- हरिश की मासिक बचत = 20000 - 9000 = 11000।
- शालिनी की मासिक आय = 191520/12 = 15960
- शालिनी की मासिक बचत = 15960 - 9000 = 6960
- इसलिए, हरिश की बचत का अनुपात शालिनी की बचत के प्रति = 11000/6960 = 1.58046
एकात्मक विधि के उपयोग
एकात्मक विधि का हमारे दैनिक जीवन में विभिन्न समस्याओं को हल करने में व्यापक उपयोग होता है। इसके मुख्य उपयोग निम्नलिखित हैं।
- किसी मात्रा का प्रतिशत निकालने के लिए इसका उपयोग किया जाता है।
- किसी निर्धारित कार्य को पूरा करने के लिए आवश्यक जनशक्ति ज्ञात की जा सकती है।
- यदि एक वर्ग के क्षेत्रफल और भुजा का अनुपात दिया गया है, तो हम उस वर्ग का क्षेत्रफल एकात्मक विधि से ज्ञात कर सकते हैं।
- यदि किसी वस्तु की लागत और मात्रा दी गई है, तो इसकी लागत ज्ञात करने में मदद करता है।
- यह हमें दिए गए दूरी के लिए किसी वाहन की गति की गणना करने में भी मदद करता है।
उदाहरण 4: 2 नोटबुक की लागत Rs. 90 है। 10 नोटबुक की लागत ज्ञात करें। समाधान: हमारे पास दी गई मात्रा 2 है और इन 2 मात्रा की कीमत Rs. 90 है। पहले हम 1 मात्रा की कीमत ज्ञात करते हैं, फिर हम 10 नोटबुक की कीमत ज्ञात करते हैं। 10 नोटबुक की लागत = 1 नोटबुक की लागत × 10 पुस्तकों की संख्या = 45 × 10 = Rs 450। इस प्रकार हमें 10 नोटबुक की लागत मिलती है अर्थात् Rs. 450।
उदाहरण 5: निम्नलिखित विकल्पों में से कौन सा लागत प्रभावी है?
- (i) बोतल A की कीमत 2 लीटर के लिए ₹55 है
- (ii) बोतल B की कीमत 3 लीटर के लिए ₹70 है
- (i) 1 लीटर की लागत = 55/2 = ₹27.5
- (ii) 1 लीटर की लागत = 70/3 = ₹23.3
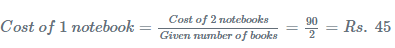
|
142 videos|172 docs|185 tests
|




















