अवलोकन: समय और कार्य | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
समय और कार्य एक महत्वपूर्ण विषय है जो प्रतियोगी परीक्षाओं में महत्वपूर्ण है। समय और कार्य से संबंधित प्रश्नों का विभिन्न अनुप्रयोगों के कारण महत्वपूर्ण वजन होता है।

समय और कार्य उस समय से संबंधित है जो एक व्यक्ति या व्यक्तियों के समूह को एक कार्य को पूरा करने में लगता है और उनके द्वारा किए गए कार्य की दक्षता।
समय और कार्य के समस्याएँ दो श्रेणियों में आती हैं:
- निर्धारित कार्य को पूरा करने के लिए आवश्यक समय खोजना।
- दिए गए समय अवधि में किए गए कार्य को खोजना।
समय और कार्य क्या है?
- कार्य को परिभाषित किया गया है कि यह कुछ ऐसा है जिसका प्रभाव या परिणाम है; अक्सर वह जो वांछित या अपेक्षित होता है।
- समय और कार्य का मूलभूत सिद्धांत सभी अंकगणितीय विषयों में समान है, अर्थात्, अनुपात का सिद्धांत।
- जब कार्य की मात्रा स्थिर होती है, तो दक्षता समय के लिए विपरीत अनुपात में होती है। अर्थात्, दक्षता ∝ 1/समय लिया गया।
यदि एक व्यक्ति 'n' दिनों में कार्य पूरा कर सकता है, तो 1 दिन में किया गया कार्य = 1/n, और इस एक दिन के कार्य को प्रतिशत के रूप में क्षमता कहा जाता है।
- यदि एक व्यक्ति एक दिन में 1/n कार्य पूरा कर सकता है, तो वह पूरे कार्य को n दिनों में पूरा कर सकता है। यहाँ, हम मानते हैं कि कुल कार्य एक (इकाई) है; निर्धारित कार्य पूरा करने के लिए आवश्यक दिनों की संख्या दिन के कार्य के व्युत्क्रमी के समान होगी।
यदि A अपने कार्य को a दिनों में पूरा कर सकता है, तो A का एक दिन का कार्य = 1/a
यदि B अपना कार्य b दिनों में पूरा कर सकता है, तो B का एक दिन का कार्य = 1/b है। यदि A और B एक साथ एक दिन में काम करते हैं, तो उनका संयुक्त कार्य 1/a + 1/b या (a*b)/(a+b) होगा।
इस प्रकार की समस्याओं को तीन तरीकों से हल किया जा सकता है:
- यूनिटरी पद्धति
- प्रतिशत क्षमता
- LCM दृष्टिकोण (सर्वश्रेष्ठ दृष्टिकोण)
यूनिटरी पद्धति पुराने जमाने की है क्योंकि इसमें गणनाएँ कठिन होती हैं।
नोट:
- ज्यादा लोग, कम दिन और विपरीत रूप से, कम लोग, ज्यादा दिन।
- ज्यादा लोग, ज्यादा कार्य और विपरीत रूप से, ज्यादा कार्य, ज्यादा लोग।
- ज्यादा दिन, ज्यादा कार्य और विपरीत रूप से, ज्यादा कार्य, ज्यादा दिन।
दृष्टिकोण
1. प्रतिशत दृष्टिकोण
कुल कार्य का मान 1 कार्य की इकाई मानने के बजाय, हम कुल कार्य को कार्य का 100 प्रतिशत भी मान सकते हैं। ऐसी स्थिति में निम्नलिखित नियम लागू होता है:
- यदि A एक कार्य a दिनों में करता है, तो एक दिन में A 100/a % कार्य करता है।
- यदि B एक कार्य b दिनों में करता है, तो एक दिन में B 100/b % कार्य करता है।
- फिर, एक दिन में, यदि A और B एक साथ काम करते हैं, तो उनका संयुक्त कार्य 100/a + 100/b होगा।
उदाहरण: यदि A एक कार्य 10 दिनों में कर सकता है और B वही कार्य 12 दिनों में कर सकता है, तो वह कार्य कितने दिनों में पूरा होगा?
हल: A का एक दिन का कार्य = 100/10 % = 10%, B का एक दिन का कार्य = 100/12 % = 8.33%। एक दिन में कुल कार्य = 10% + 8.33% = 18.33%। कुल दिनों की आवश्यकता = 100/18.33 ≈ 5.45 दिन।
2. LCM विधि (सर्वश्रेष्ठ दृष्टिकोण)
LCM विधि को एक उदाहरण के माध्यम से सबसे अच्छे तरीके से समझाया जा सकता है। आइए ऊपर दिए गए उदाहरण का ही उपयोग करें।
उदाहरण: यदि A एक कार्य को 10 दिनों में कर सकता है और B उसी कार्य को 12 दिनों में कर सकता है, तो कार्य कितने दिनों में पूरा होगा?
समाधान: 10 और 12 का LCM लें, अर्थात 60। इसे कुल कार्य मान लें। A कार्य को 10 दिनों में कर सकता है; इसलिए, वह प्रतिदिन 6 इकाइयाँ कार्य करेगा (60/10)। B कार्य को 12 दिनों में कर सकता है; इसलिए, वह प्रतिदिन 5 इकाइयाँ कार्य करेगा (60/12)।
- प्रतिदिन कुल कार्य की इकाइयाँ = 6 + 5 = 11
- कुल दिनों की आवश्यकता = कुल कार्य / प्रतिदिन संयुक्त कार्य = 60 / 11 = 5.45
नकारात्मक कार्य का सिद्धांत
- मान लें कि X और Y मिलकर एक दीवार बना रहे हैं लेकिन Z दीवार को तोड़ने का कार्य कर रहा है। इस स्थिति में दीवार X और Y द्वारा बनाई जा रही है लेकिन Z द्वारा तोड़ी जा रही है। यदि हम दीवार बनाने के कार्य को सकारात्मक मानते हैं, तो हम कह सकते हैं कि Z नकारात्मक कार्य कर रहा है।
- गणितीय रूप से, यदि 1 व्यक्ति किसी चीज़ को A दिनों में बनाता है और दूसरा उसे B दिनों में तोड़ता है, तो:
- प्रतिदिन किया गया कार्य = 1/A - 1/B = (B-A)/AB
- दिनों की संख्या = AB/(B-A)
उदाहरण: अमित एक दीवार को 6 घंटे में बना सकता है लेकिन रोहित उसे 10 घंटे में नष्ट कर सकता है। यदि दोनों एक साथ काम करते हैं, तो दीवार को वास्तव में बनाने के लिए कितने घंटे की आवश्यकता होगी?
समाधान: अमित दीवार को 6 घंटे में बनाता है (सकारात्मक कार्य) और रोहित दीवार को 10 घंटे में नष्ट करता है (नकारात्मक कार्य)।
अमित द्वारा 1 घंटे में किया गया कार्य = 1/6
रोहित द्वारा 1 घंटे में किया गया कार्य = 1/10
प्रति घंटे किया गया कार्य = 1/6 - 1/10 = 2/30 = 1/15
दीवार को पूरा करने के लिए आवश्यक घंटे = 15 घंटे
उत्पाद स्थिरता तालिका का अनुप्रयोग
समय और कार्य के लिए जो मूल समीकरण लागू होता है वह है: कार्य किया गया = कार्य दर x समय
- यह समीकरण दर्शाता है कि जब कार्य किया गया समान होता है, तो कार्य दर समय के साथ विपरीत रूप से बदलती है।
- इस प्रकार, उत्पाद स्थिरता तालिका का सीधा उपयोग समय और कार्य के प्रश्नों के साथ किया जाएगा।
- समय आमतौर पर दिन या घंटे में होता है।
- कार्य दर के प्रश्न में उपयोग की जाने वाली समय की इकाई आमतौर पर कार्य दर की इकाई के हर में निर्धारित होती है।
- इसलिए, कार्य दर को परिभाषित करने के लिए दो तरीके हैं।
- व्यक्तिगत कार्य दक्षताएँ: उन प्रश्नों में जहां व्यक्तिगत कार्य दक्षताएँ या व्यक्तिगत कार्य समय दिया गया है, कार्य दर को इस प्रकार परिभाषित किया जाता है: कार्य किया गया/समय।
- इस मामले में, कुल कार्य को 1 (यदि हम भिन्नों के माध्यम से हल करते हैं) और 100% (यदि हम प्रतिशत के माध्यम से हल करते हैं) माना जाता है।
उदाहरण: यदि A एक कार्य को 10 दिनों में कर सकता है और B वही कार्य 12 दिनों में कर सकता है। A और B मिलकर कार्य कितने दिनों में कर सकते हैं?
हल: हम इस प्रश्न को प्रतिशत विधि के माध्यम से हल करेंगे। एक दिन का कार्य = 10% + 8.33% = 18.33%। इसलिए, A और B मिलकर एक दिन में 18.33% कार्य करते हैं। इस प्रकार, हम कह सकते हैं कि 18.33% कार्य x आवश्यक दिन की संख्या = 100% कार्य। आवश्यक दिन की संख्या = 100/18.33 = 5.45। इसलिए, हमने निष्कर्ष निकाला कि जब व्यक्तिगत कार्य दिया जाता है, तो हम कार्य दर को कार्य किया गया/समय के रूप में परिभाषित करते हैं और कुल कार्य = 100% या 1 मानते हैं।
- कार्य एक निश्चित श्रेणी के श्रमिकों द्वारा पूरे होते हैं। इस प्रकार में जहां एक निश्चित श्रेणी के श्रमिक किसी कार्य या परियोजना पर काम कर रहे हैं, कार्य दर को परियोजना पर काम कर रहे विशेष श्रेणी के श्रमिकों की संख्या के रूप में परिभाषित किया जाएगा। ऐसे मामलों में, किया जाने वाला कार्य आवश्यक घंटे की संख्या के रूप में लिया जाता है।
कार्य समकक्षता विधि
- कार्य समकक्षता विधि कुछ नहीं बल्कि समय और कार्य समस्याओं का एक महत्वपूर्ण अनुप्रयोग है। हम पहले से ही सूत्र जानते हैं अर्थात् कार्य दर x समय = किया गया कार्य। अब, कार्य समकक्षता विधि कहती है कि यदि हम किया गया कार्य दोगुना करते हैं, तो (कार्य दर x समय) को भी दोगुना होना चाहिए। इसी तरह, यदि किया गया कार्य 20% बढ़ाना है, तो उत्पाद (कार्य दर x समय) को भी 20% बढ़ाना चाहिए और ऐसा ही आगे बढ़ाना चाहिए।
उदाहरण: एक बढ़ई का अनुमान है कि वह 50 पुरुषों को empley करके अपने परियोजना को 100 दिनों में पूरा करेगा। हालांकि, 50वें दिन के अंत में, जब उसके अनुमान के अनुसार आधा कार्य पूरा हो जाना चाहिए था, उसे पता चलता है कि केवल 40% कार्य पूरा हुआ है।
- क. कार्य पूरा करने के लिए और कितने दिन की आवश्यकता होगी?
- ख. क्या उसे अपने कार्य को समय पर पूरा करने के लिए और कितने पुरुषों की आवश्यकता होगी?
समाधान: a) कारपेंटर ने 50 दिनों में अपने कार्य का 40% पूरा किया है। यदि पुरुषों की संख्या समान रहती है, तो जिस दर पर कार्य चल रहा है वह समान रहेगा। इसलिए, शेष कार्य अर्थात 60% कार्य को पूरा करने में 75 दिन लगेंगे (इसे युनिटरी विधि का उपयोग करके हल किया गया)। इसलिए, पूरे प्रोजेक्ट को पूरा करने के लिए 75 और दिन की आवश्यकता है। b) अब, यदि वह समय पर कार्य पूरा करना चाहता है, तो उसे प्रोजेक्ट पर अधिक पुरुषों को नियुक्त करना होगा। 50 पुरुष 50 दिनों के लिए काम कर रहे हैं = 2500 व्यक्ति-दिन => 2500 व्यक्ति-दिन 40% कार्य पूरा करने के लिए आवश्यक हैं। शेष कार्य = 60% शेष कार्य को पूरा करने में = 2500 x 60/40 = 2500 x 1.5 = 3750 व्यक्ति-दिन। इसे 50 दिनों में पूरा करना है, इसलिए, पुरुषों की संख्या = 3750 / 50 = 75 पुरुष।
चूंकि 50 पुरुष पहले से काम कर रहे हैं, आवश्यक अतिरिक्त पुरुष हैं:
75 - 50 = 25 पुरुष
पाइप और जलाशय
- हम पाइप और जलाशयों पर आधारित प्रश्नों को हल करने के लिए ‘समय और कार्य’ के उसी मूलभूत सिद्धांत का उपयोग करते हैं। हालांकि, कुछ मामलों में इनलेट पाइप के अलावा, प्रश्न में आउटलेट पाइप भी उल्लेखित होते हैं।
- एक पाइप जो जलाशय से जुड़ी होती है, उसे इनलेट पाइप या आउटलेट पाइप कहा जाता है, जो इसे भरती है या इसे खाली करती है।
- यहां कार्य और समय के सिद्धांत को लागू करने के लिए, हम मानते हैं कि इनलेट पाइप सकारात्मक कार्य कर रहे हैं और आउटलेट पाइप नकारात्मक कार्य कर रहे हैं और इन प्रश्नों को हल करने का सिद्धांत समान रहता है।
उदाहरण: दो पाइप A और B क्रमशः 20 और 30 मिनट में एक टैंक भर सकते हैं, और तीसरी पाइप C इसे 40 मिनट में खाली कर सकती है। यदि तीनों पाइप एक साथ खोली जाती हैं, तो टैंक भरने में कितना समय लगेगा?
हल: 20, 30 और 40 का LCM = 120। मान लेते हैं कि टैंक की क्षमता 120 लीटर है। इसलिए, पाइप A की दर = 120/20 = 6 लीटर/मिनट। इसी प्रकार, पाइप B की दर = 120/30 = 4 लीटर/मिनट। और पाइप C की दर = 120/40 = 3 लीटर/मिनट। यदि तीनों पाइप एक साथ खोले जाते हैं, तो एक मिनट में टैंक में पानी की मात्रा = 6 + 4 - 3 = 7 लीटर होगी। चूंकि पाइप C एक आउटलेट पाइप है, हम इसके कार्य को नकारात्मक मान रहे हैं। अतः, टैंक को भरने में समय = 120/7 मिनट। इसलिए, उपरोक्त व्याख्या से यह स्पष्ट है कि पाइप और टंकियों की समस्याएँ कार्य और समय का विस्तार हैं।
पाइप और टंकियों के महत्वपूर्ण सिद्धांत
1. टैंक को खाली करने के लिए लीक पाइप द्वारा आवश्यक समय
- यदि एक इनलेट पाइप को एक टंकी भरने में 'x' मिनट लगते हैं,
- लेकिन लीक के कारण, इसे टंकी भरने में अतिरिक्त 'y' मिनट लगते हैं,
- तो, लीक के द्वारा पूरी टंकी को खाली करने में लगने वाला समय मिनटों में है।
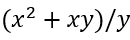
उदाहरण: यदि एक टैंक को सामान्यतः भरने के लिए 20 मिनट लगते हैं, लेकिन लीक के कारण, इसे भरने में 10 अतिरिक्त मिनट लगते हैं, तो लीक को पूरी टंकी को खाली करने में कितना समय लगेगा? हल: तुलना करने पर, हमें x=20 और y=10 मिलते हैं। इसलिए, लीक को मिनटों में लगेगा। x और y के मान डालने पर, हमें प्राप्त होता है (20 * 20)/(20 + 10) = 60 मिनट।
2. टैंक की क्षमता ज्ञात करना
एक जलाशय में एक रिसाव है जो इसे 'a' घंटों में खाली कर सकता है। एक पाइप जो प्रति घंटे 'b' लीटर पानी जलाशय में डालता है, चालू किया जाता है, और अब जलाशय 'c' घंटों में खाली होता है। फिर जलाशय की क्षमता लीटर में है: (a x b x c)/(c-a)
उदाहरण : एक टैंक में एक रिसाव है जो इसे 4 घंटों में खाली कर सकता है। एक पाइप जो प्रति घंटे 20 लीटर पानी टैंक में डालता है, चालू किया जाता है, और अब टैंक 6 घंटों में खाली होता है। टैंक की क्षमता क्या है?
हल: शॉर्टकट फ़ॉर्मूले की तुलना करते हुए, a=4, b=20, और c=6। इसलिए, टैंक की क्षमता = (a x b x c)/(c-a) में a, b और c के मान डालने पर, हमें मिलता है (4x20x6)/(6-4) = 240 लीटर।
3. विभिन्न समयावधियों के लिए खोली गई पाइपें: यदि दो पाइप A और B विभिन्न समयावधियों के लिए खोले जाते हैं, तो प्रश्न को हल करने के लिए हम उपयोग करते हैं A का कार्य / B का कार्य = 1। (A का खुला समय / A का अकेले भरने का समय) (B का खुला समय / B का अकेले भरने का समय) = 1
उदाहरण : दो पाइप A और B क्रमशः 12 और 16 मिनट में एक जलाशय भर सकते हैं। दोनों पाइप एक साथ खोले जाते हैं लेकिन जलाशय भरने से 4 मिनट पहले, एक पाइप A बंद कर दी जाती है। जलाशय भरने में कितना समय लगता है?
हल: मान लीजिए कि पाइप A और B को जलाशय भरने में x मिनट लगते हैं। इसलिए, पाइप के संचालन की अवधि = (x-4) मिनट। और पाइप B का संचालन x मिनट रहा। अब, उपरोक्त फ़ॉर्मूले में डालते हैं, हमें मिलता है: (x-4)/12 x/16 = 1 (4x-16 3x)/48 = 1 x = 64/7 मिनट। इसलिए, जलाशय भरने में 64/7 मिनट लगते हैं।
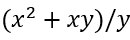
4. पाइप का प्रवाह दर व्यास के समानुपाती है। उदाहरण: तीन इनलेट पाइप हैं जिनका व्यास क्रमशः 1 सेमी, 2 सेमी, और 4 सेमी है। पानी का प्रवाह दर व्यास के वर्ग के सीधे समानुपाती होता है। सबसे बड़े व्यास वाली पाइप को एक टंकी भरने में 16 मिनट लगते हैं। तीनों पाइपों के एक साथ काम करने पर टंकी भरने में कितना समय लगेगा।
हल: मान लीजिए कि तीन पाइप A, B, और C हैं। इसलिए, पाइप A के लिए, प्रति मिनट प्रवाह दर = k(1)2 = k। इसी तरह, पाइप B की प्रति मिनट प्रवाह दर = k(2)2 = 4k और, पाइप C की प्रति मिनट प्रवाह दर = k(4)2 = 16k, जहाँ k एक समानुपातिक स्थिरांक है। यह दिया गया है कि पाइप C अकेले टंकी भरने में 16 मिनट लेती है। इसलिए, टंकी की क्षमता = पाइप C का प्रवाह दर × पाइप C द्वारा लिया गया समय = 16k × 16 = 256k लीटर। अब, जब तीनों पाइप एक साथ काम करती हैं, तो प्रति मिनट संयुक्त प्रवाह दर = k + 4k + 16k = 21k। इसलिए, टंकी भरने के लिए आवश्यक समय = 256k / 21k = 256 / 21 मिनट।
महत्वपूर्ण सूत्र
प्रकार - 1: मूल सूत्र
- यदि M1 पुरुष W1 कार्य को D1 दिनों में कर सकते हैं और M2 पुरुष W2 कार्य को D2 दिनों में कर सकते हैं, तो:
- यदि हम दो समूहों के लिए कार्य करने के घंटे T1 और T2 को शामिल करते हैं, तो:
- यदि M1 पुरुष E1 दक्षता के साथ W1 कार्य को D1 दिनों में T1 कार्य घंटे/दिन के साथ कर सकते हैं और M2 पुरुष E2 दक्षता के साथ W2 कार्य को D2 दिनों में T2 कार्य घंटे/दिन के साथ कर सकते हैं, तो:
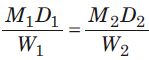
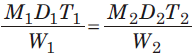
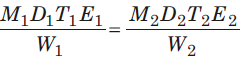
चलिये कुछ उदाहरणों पर नज़र डालते हैं।

उदाहरण 1: एक ठेकेदार एक कार्य को 100 दिनों में पूरा करने के लिए कार्य करता है। उसने 100 श्रमिकों को काम पर रखा। लेकिन 50 दिनों के बाद यह पाया गया कि केवल 1/3 कार्य पूरा हुआ है। समय पर कार्य पूरा करने के लिए उसे और कितने श्रमिकों को काम पर रखना चाहिए? (क) 100 (ख) 125 (ग) 150 (घ) 175
उदाहरण 1: यदि 25 पुरुष 10 घंटे काम करते हुए 36 दिनों में एक काम कर सकते हैं, तो 20 दिनों में 6 घंटे काम करते हुए उस काम को पूरा करने के लिए कितने पुरुषों की आवश्यकता होगी? (a) 65 (b) 75 (c) 84 (d) 92
उत्तर: विकल्प (b) सही है।
उदाहरण 2: एक ठेकेदार ने एक निश्चित संख्या में श्रमिकों को एक सड़क का निर्माण खत्म करने के लिए नियुक्त किया। कुछ समय बाद, जब एक भाग का काम पूरा हो चुका था, उसे एहसास हुआ कि काम निर्धारित समय के तीन-चौथाई समय तक देरी हो जाएगी, इसलिए उसने तुरंत श्रमिकों की संख्या को दोगुना कर दिया और इस प्रकार उसने सड़क को निर्धारित समय पर पूरा किया। काम बढ़ाने से पहले कितना काम पूरा हुआ था?
- (a) 10%
- (b) 12%
- (c) 15%
प्रकार - 2: जब 2 व्यक्ति काम कर रहे हों
यदि A एक काम को x दिनों में और B उसी काम को y दिनों में कर सकता है, तो A और B मिलकर उसी काम को (x * y) / (x + y) दिनों में करेंगे। आइए इसके कुछ उदाहरण देखते हैं।
उदाहरण 4: A और B 12 दिनों में काम कर सकते हैं, B और C 15 दिनों में, C और A 20 दिनों में। प्रत्येक को अलग-अलग उस काम को करने में कितना समय लगेगा? (a) A = 20 दिन, B = 30 दिन, C = 50 दिन (b) A = 30 दिन, B = 20 दिन, C = 60 दिन (c) A = 20 दिन, B = 20 दिन, C = 50 दिन (d) A = 30 दिन, B = 40 दिन, C = 30 दिन
प्रकार - 3: जब 3 व्यक्ति काम कर रहे हों
यदि A, B, और C क्रमशः x, y, और z दिनों में काम करते हैं, तो तीनों मिलकर काम को 1 / (1/x + 1/y + 1/z) दिनों में पूरा कर सकते हैं।
आइए एक उदाहरण देखें।
उदाहरण 5: A 10 दिनों में काम पूरा कर सकता है, B 20 दिनों में और C 25 दिनों में। यदि वे एक साथ काम करते हैं, तो वे कितने दिनों में काम पूरा कर सकते हैं? (a) (b) (c) (d)
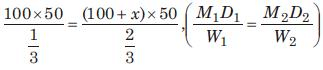
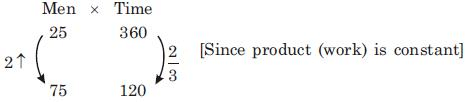
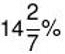
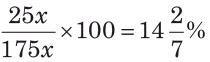
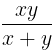

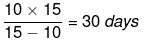
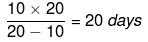
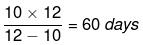
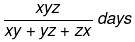
प्रकार - 4: अकेले काम करने के लिए कितने दिन?
यदि A और B मिलकर किसी काम को x दिनों में पूरा कर सकते हैं और A अकेला इसे y दिनों में कर सकता है, तो B अकेला इसे xy/(y-x) दिनों में कर सकता है। आइए एक उदाहरण से समझते हैं।
उदाहरण 6: टाप M द्वारा टैंक भरने की दर टाप N की दर से 60% अधिक है। यदि दोनों टाप एक साथ खोले जाएं, तो वे टैंक को भरने में 50 घंटे लेते हैं। N अकेला टैंक भरने में कितना समय लेता है (घंटों में): (क) 90 घंटे (ख) 110 घंटे (ग) 130 घंटे (घ) 150 घंटे
उत्तर: विकल्प 'ग' सही है।
समाधान: चूंकि टाप M द्वारा टैंक भरने की दर टाप N की दर से 60% अधिक है, इसलिए टाप M द्वारा टैंक भरने की दर N की दर का 1.6 गुना है। अतः, टाप M द्वारा टैंक भरने की दर 1.6x इकाइयाँ प्रति घंटे है। जब दोनों टाप एक साथ खोले जाते हैं, तो वे टैंक को 50 घंटे में भर सकते हैं। इसलिए, दोनों टापों की संयुक्त दर 1 टैंक प्रति 50 घंटे या 1/50 टैंक प्रति घंटे है। संयुक्त दर व्यक्तिगत दरों का योग है: x (N की दर) + 1.6x (M की दर) = 1/50
अब, x के लिए हल करें:
x = (1/50) / 2.6
x = 1/50 * 1/2.6
x = 1/130
इसलिए, टाप N प्रति घंटे 1/130 टैंक भरता है।
अब, N अकेले टैंक भरने में लगने वाले समय को खोजने के लिए, इसकी दर का व्युत्क्रम लें:
N अकेले द्वारा लिया गया समय = 1 / (1/130)
N अकेले द्वारा लिया गया समय = 130 घंटे
इसलिए, टाप N को अकेले टैंक भरने में 130 घंटे लगते हैं।
प्रकार - 5: समय और काम के बीच परिवर्तन
- जब एक मात्रा का मान दूसरी मात्रा की कमी के सापेक्ष बढ़ता है या इसके विपरीत, तो उन्हें विपरीत अनुपात में कहा जाता है। इसका मतलब है कि ये दो मात्राएँ स्वभाव से विपरीत व्यवहार करती हैं। कार्य को पूरा करने के लिए आवश्यक दिनों (D) की संख्या के साथ दक्षता विपरीत अनुपात में होती है। अर्थात्, E ∝ 1/D या E = K/D जहाँ K एक स्थिरांक है ∴ ED = स्थिरांक। इसी प्रकार, E1D1 = E2D2।
- ये उत्पाद विधियाँ स्थिर कार्य के लिए सीमित हैं, यदि कार्य की मात्रा बदलती है, तो यह काम नहीं करती, तब हमें एकक विधि से सहायता लेनी होती है।
- एकक विधि में, पहले एक मात्रा की एकक का मान निकलकर अन्य इकाइयों का मूल्य निकाला जाता है। इसमें दो प्रकार के परिवर्तन होते हैं: (i) प्रत्यक्ष परिवर्तन: प्रत्यक्ष परिवर्तन में, एक मात्रा में वृद्धि या कमी दूसरी मात्रा में वृद्धि या कमी का कारण बनती है। उदाहरण के लिए, सामान की संख्या में वृद्धि होने पर कीमत अधिक होगी। (ii) विपरीत परिवर्तन: यह प्रत्यक्ष परिवर्तन का विपरीत है। यदि हम एक मात्रा को बढ़ाते हैं, तो दूसरी मात्रा का मान घट जाता है।
उदाहरण 7: A अकेले एक कार्य को पूरा करने में 16 दिन लगाता है, जबकि B वही कार्य 8 दिन में पूरा करता है। उनकी दक्षता का अनुपात क्या है और कौन कम दक्ष है? (क) 1 : 2 (ख) 1 : 3 (ग) 2 : 3 (घ) 3 : 4
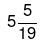
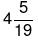
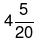
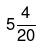
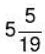
यदि आपको "समय और कार्य" विषय पर अभ्यास प्रश्नों को समझने के लिए शिक्षक की मदद चाहिए, तो नीचे दिए गए वीडियो को देखें:
आइए "समय और कार्य" पर कुछ प्रश्नों का अभ्यास करते हैं।
अभ्यास प्रश्न
प्रश्न 1: A एक कार्य को 10 दिनों में, B 12 दिनों में और C 15 दिनों में पूरा कर सकता है। सभी ने मिलकर कार्य शुरू किया, लेकिन A को कार्य शुरू करने के 2 दिन बाद छोड़ना पड़ा और B को कार्य की समाप्ति से 3 दिन पहले छोड़ना पड़ा। कार्य कितने दिन चला?
- (a) 5
- (b) 6
- (c) 7
- (d) 8
उत्तर: विकल्प (c) सही है।
प्रश्न 2: अरुण और सत्या व्यक्तिगत रूप से 12 दिन और 15 दिन में कार्य पूरा कर सकते हैं। अरुण केवल सोमवार, बुधवार और शुक्रवार को काम करता है जबकि सत्या मंगलवार, गुरुवार और शनिवार को काम करता है। रविवार हमेशा छुट्टी होती है। लेकिन अरुण और सत्या क्रमशः शुक्रवार और शनिवार को अपनी आधी क्षमता से काम करते हैं। यदि अरुण ने 1 जनवरी को काम शुरू किया, जो कि सोमवार है, उसके बाद सत्या अगले दिन काम शुरू करता है और इसी तरह (अर्थात वे वैकल्पिक दिनों पर मिलकर काम करते हैं), तो कार्य किस दिन पूरा होगा?
- (a) मंगलवार
- (b) गुरुवार
- (c) शुक्रवार
- (d) शनिवार
हल: यह पैटर्न कुल 2 सप्ताह तक जारी रहा जब तक 75% कार्य पूरा नहीं हुआ।
इस प्रकार, 2 सप्ताह में वे 75% कार्य पूरा करेंगे।
अब शेष 25% कार्य में से 15% तीसरे सप्ताह के सोमवार और मंगलवार को किया जाएगा। फिर 10% कार्य अधूरा रह जाएगा। इसमें से 8.33% कार्य बुधवार को अरुण द्वारा किया जाएगा और शेष 1.66% कार्य शुक्रवार को सत्या द्वारा पूरा किया जाएगा।
इसलिए कार्य गुरुवार को पूरा होगा।
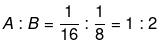
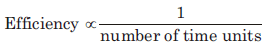
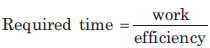
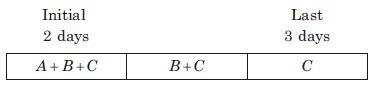

प्रश्न 3: प्राचीन शहर पोर्थियस में, सम्राट ने एक ओवरहेड टैंक स्थापित किया है जिसे दो पंप X और Y भरते हैं। X टैंक को 12 घंटे में भर सकता है जबकि Y टैंक को 15 घंटे में भर सकता है। एक पाइप Z है जो टैंक को 10 घंटे में खाली कर सकता है। दोनों पंप एक साथ खोले जाते हैं। टैंक के पर्यवेक्षक, कार्य पर जाने से पहले, अपने सहायक से कहते हैं कि जब टैंक ठीक 40% भरा हो जाए, तब Z को खोल दें ताकि जब वह वापस आएं, तो टैंक पूरी तरह से भरा हो। यदि वह X और Y को ठीक 11:00 AM पर शुरू करता है और वह A: B पर वापस आता है। तो A और B का मान ज्ञात करें।
- (a) 40
- (b) 41
- (c) 42
- (d) 43
उत्तर: विकल्प (b) सही है।
प्रश्न 4: तीन पाइप, A, B और C, क्रमशः 12, 18 और 24 मिनट में एक टैंक को भर सकते हैं। यदि सभी पाइप 7 मिनट के लिए एक साथ खोले जाते हैं, तो टैंक की कुल मात्रा के प्रतिशत के रूप में कितना पानी बह जाएगा?
- (a)
- (b)
- (c)
- (d)
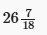
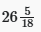
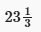
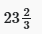
कुल कार्य = 72
पाइप A, B और C द्वारा 7 मिनट में किया गया कार्य = (6 + 4 + 3) × 7 = 91
जो पानी बह गया उसकी मात्रा = 91 – 72 = 19
आवश्यक प्रतिशत = (19/72) × 100 =
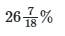
प्रश्न 5: एक अनुबंध को 72 दिनों में पूरा करना है और 104 पुरुषों को काम पर लगाया गया है, प्रत्येक 8 घंटे प्रति दिन काम करते हैं। 30 दिनों के बाद, केवल 1/5 कार्य पूरा हुआ है। समय पर कार्य पूरा करने के लिए कितने अतिरिक्त पुरुषों की आवश्यकता है? (यदि अब प्रत्येक पुरुष 9 घंटे प्रति दिन काम कर रहा है)?
- (a) 153 पुरुष
- (b) 155 पुरुष
- (c) 158 पुरुष
- (d) 161 पुरुष
उत्तर: विकल्प (d) सही है।
हल: कार्य समकक्षता विधि का उपयोग करते हुए, हमें पता है कि 1/5 कार्य = 104 x 30 x 8 पुरुष-घंटे।
इस प्रकार, शेष कार्य = 4 x 104 x 30 x 8। चूंकि यह कार्य शेष 42 दिनों में 9 घंटे प्रति दिन काम करके करना है, आवश्यक व्यक्तियों की संख्या होगी: (4 x 104 x 30 x 8) ÷ (42 x 9) = 264.12 = 265 व्यक्ति। इसका मतलब है कि हमें 161 अतिरिक्त व्यक्तियों को नियुक्त करने की आवश्यकता होगी।
प्रश्न 6: दो नल एक जलाशय को क्रमशः 14 और 16 घंटे में भर सकते हैं। नल एक साथ खोले जाते हैं और यह पाया जाता है कि जलाशय में रिसाव के कारण इसे भरने में 32 मिनट का अतिरिक्त समय लगता है। जब जलाशय भर जाता है, तो रिसाव इसे कितने समय में खाली करेगा?
हल: 32 मिनट अतिरिक्त समय उस अतिरिक्त समय का प्रतिनिधित्व करता है जो नलों ने रिसाव के कारण लिया।
नलों के लिए सामान्य समय → n * (1/14 + 1/16) = 1 → n = 112 / 15 = 7 घंटे 28 मिनट।
इस प्रकार, 32 मिनट अतिरिक्त समय के साथ, नल टैंक को भरने में 8 घंटे लेंगे।
इस प्रकार, 8(1/14 + 1/16) - 8 * (1/L) = 1 → 8 / L
= 8(15 / 112) - 1
1/L = 15 / 112 - 1/8
= 1/112।
इस प्रकार, L = 112 घंटे।
|
142 videos|172 docs|185 tests
|
















