कक्षा 6 गणित: नमूना पत्र समाधान - 4 | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download
सामान्य निर्देश:
सभी प्रश्न अनिवार्य हैं।
- अनुभाग A में 12 प्रश्न हैं, प्रत्येक 1 अंक के लिए।
- अनुभाग B में 10 प्रश्न हैं, प्रत्येक 2 अंकों के लिए।
- अनुभाग C में 8 प्रश्न हैं, प्रत्येक 3 अंकों के लिए।
- अनुभाग D में 2 प्रश्न हैं, प्रत्येक 5 अंकों के लिए।
Q1: यदि एक त्रिकोण का आधार दोगुना किया जाता है जबकि ऊँचाई वही रहती है, तो क्षेत्रफल में कैसे परिवर्तन होता है? (1 अंक)
- (a) वही रहता है
- (b) दोगुना हो जाता है
- (c) तिगुना हो जाता है
- (d) आधा हो जाता है
Q2: एक दुकानदार एक दिन ₹30 कमाता है और अगले दिन ₹45 खोता है। उसका कुल लाभ या हानि क्या है? (1 अंक)
- (a) ₹15 लाभ
- (b) ₹75 हानि
- (c) ₹15 हानि
- (d) ₹45 लाभ
Q3: निम्नलिखित में से कौन सा समरूपता की धुरी को सबसे अच्छे से वर्णन करता है? (1 अंक)
- (a) एक बिंदु जहाँ आकार घूमता है
- (b) एक रेखा जो एक आकृति को दो दर्पण छवि भागों में बांटती है
- (c) एक आकार के केंद्र से उसके किनारे तक की दूरी
- (d) घुमाव के कोण का माप
Q4: डेटा हैंडलिंग में आवृत्ति क्या दर्शाती है? (1 अंक)
- (a) कुल ग्राफ की संख्या
- (b) मानों, मापों या अवलोकनों की संख्या
- (c) चित्रात्मक ग्राफ में रंगों की संख्या
- (d) बार ग्राफ की लंबाई
Q5: 15/25 को इसके न्यूनतम रूप में सरल करें। (1 अंक)
- (a) 5/10
- (b) 3/5
- (c) 2/3
- (d) 6/10
Q6: पैटर्न में अगला संख्या क्या है? (1 अंक) 2, 4, 6, 8, __?
- (a) 9
- (b) 10
- (c) 12
- (d) 14
प्रश्न 7: एक आयताकार क्षेत्र का लंबाई 15 मीटर और चौड़ाई 10 मीटर है। इसका परिमाप क्या है? (1 अंक)
- (क) 50 मीटर
- (ख) 60 मीटर
- (ग) 40 मीटर
- (घ) 45 मीटर
प्रश्न 8: पैटर्न में कौन सा संख्या गायब है? (1 अंक) 3, 6, __, 12, 15
- (क) 7
- (ख) 8
- (ग) 9
- (घ) 10
प्रश्न 9: एक आकृति जो प्रतिबिंबीय समरूपता (reflection symmetry) रखती है, उसे इसके किनारे पर दो समान भागों में विभाजित किया जा सकता है:
- (क) तिर्यक (Diagonal)
- (ख) समरूपता की रेखा (Line of symmetry)
- (ग) घूर्णन का अक्ष (Axis of rotation)
- (घ) परिमाप (Perimeter)
प्रश्न 10: निम्नलिखित में से कौन सा 12 का गुणज (factor) है? (1 अंक)
- (क) 5
- (ख) 6
- (ग) 7
- (घ) 11
प्रश्न 11: एक डाइवर्स समुद्र स्तर (0 मीटर) से शुरू होकर 25 मीटर नीचे जाता है। यदि वह फिर 10 मीटर ऊपर आता है, तो उसकी अंतिम गहराई क्या होगी? (1 अंक)
- (क) -35 मीटर
- (ख) -15 मीटर
- (ग) 15 मीटर
- (घ) 35 मीटर
प्रश्न 12: एक समकोण (right angle) का माप क्या है? (1 अंक)
- (क) 45°
- (ख) 90°
- (ग) 180°
- (घ) 360°
प्रश्न 13: एक त्रिकोण की आधार (base) 8 सेमी और ऊँचाई (height) 6 सेमी है। इसका क्षेत्रफल (area) निकालें। (2 अंक) उत्तर: त्रिकोण का क्षेत्रफल = (1/2) × आधार × ऊँचाई = (1/2) × 8 × 6 = 4 × 6 = 24 वर्ग सेमी (sq. cm)
प्रश्न 14: जब आप सभी 2 की श्रेणी को जोड़ना शुरू करते हैं, तो आपको कौन सी श्रेणी मिलती है? जब आप सभी 2 की श्रेणी को ऊपर और नीचे जोड़ते हैं, तो आपको कौन सी श्रेणी मिलती है? (2 अंक)
- सभी 2 की श्रेणी ऊपर: परिणाम गिनती के संख्याएँ हैं जो 2 से गुणा की गई हैं (2, 4, 6, 8, ...)।
- सभी 2 की श्रेणी ऊपर और नीचे: परिणाम वर्ग संख्याएँ हैं (4, 16, 36, 64, ...)।
प्रश्न 15: निम्नलिखित को ड्रॉ करें और लेबल करें: (2 अंक)
- (क) समकोण और इसे ∠ABC के रूप में लेबल करें।
- (ख) एक तीव्र कोण (acute angle) बनाएं और इसे ∠XYZ के रूप में लेबल करें।
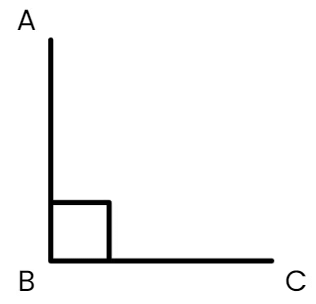
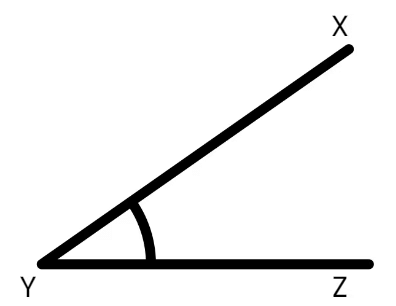
प्रश्न 16: नीचे एक माचिस की तीलियों के पैटर्न की एक श्रृंखला दी गई है। पैटर्न को ध्यान से देखें और इसे एक कदम आगे बढ़ाएं। इसके लिए एक संख्या पैटर्न भी दें: (2 अंक)
- माचिस की तीलियों की संख्या: 6, 11, 16, ___।
उत्तर: माचिस की तीलियों की संख्या: 6, 11, 16, 21।
प्रश्न 17: एक वर्गाकार खाने की मेज का एक भुजा 5 मीटर है। यदि पॉलिशिंग की लागत ₹20 प्रति वर्ग मीटर है, तो मेज को पॉलिश करने की कुल लागत क्या होगी? (2 अंक)
उत्तर: वर्गाकार मेज का क्षेत्रफल = भुजा × भुजा = 5 × 5 = 25 वर्ग मीटर
प्रति वर्ग मीटर लागत = ₹20
कुल लागत = 25 × 20 = ₹500
प्रश्न 18: संख्या 6174 को कपरेकर स्थिरांक तक पहुँचने में कितने चक्र लगते हैं? (2 अंक)
उत्तर: संख्या 6174 कपरेकर स्थिरांक है, और किसी भी 4-अंकीय संख्या (पुनरावृत्ति वाले अंकों को छोड़कर) को कपरेकर की प्रक्रिया का पालन करते हुए 6174 तक पहुँचने में अधिकतम 7 पुनरावृत्तियाँ लगती हैं।
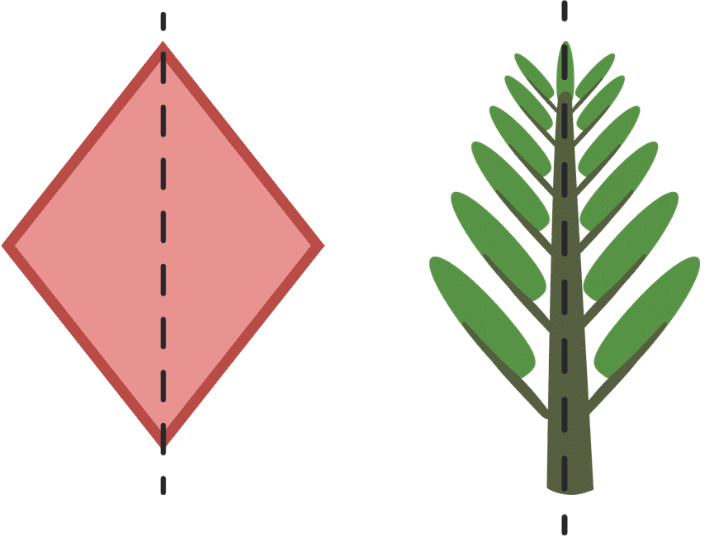
प्रश्न 19: क्या आप नीचे दिए गए चित्रों में कोई समतल रेखा देख रहे हैं? (2 अंक)
उत्तर: दोनों चित्रों में एक समतल रेखा है।
प्रश्न 20: निम्नलिखित में सही प्रतीक >, =, < डालें:="" (2="" अंक)="" (i)="" (–7)="" _________="" (2)="" (ii)="" 7="" _________="" (–12)="" (iii)="" 0="" _________="" (–2)="" (iv)="" (–16)="" _________="" (9="" />
उत्तर: (i) < (ii)="" /> (iii) > (iv)
प्रश्न 21: निम्नलिखित के लिए 'सत्य' या 'असत्य' लिखें: (2 अंक) (i) –20° C तापमान \"20°C के ऊपर\" का प्रतिनिधित्व करता है। (ii) 8 > (–10) (iii) (–2) = 2 (iv) (–4 – 2) > (–5)
उत्तर: (i) असत्य (ii) सत्य (iii) असत्य (iv) असत्य
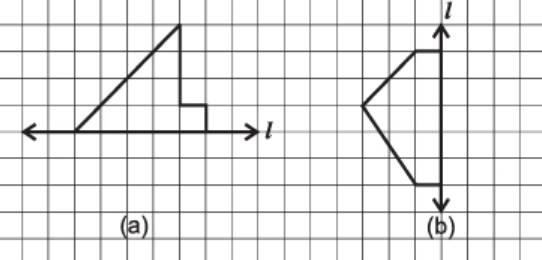
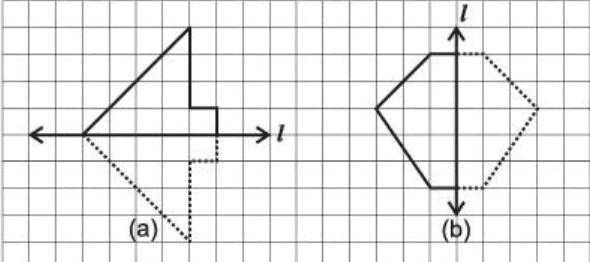
प्रश्न 22: निम्नलिखित चित्रों में, l समतल रेखा है। समरूप बनाने के लिए चित्र को पूरा करें। (2 अंक)
उत्तर:
प्रश्न 23: एक धागा 60 सेमी लंबा है। यदि धागे का उपयोग निम्नलिखित बनाने के लिए किया जाए तो प्रत्येक भुजा की लंबाई क्या होगी: (3 अंक) (क) एक वर्ग (ख) समकोण त्रिभुज (ग) एक नियमित पेंटागन
उत्तर: (क) तार की लंबाई = 60 सेमी
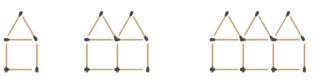


चूँकि तार का उपयोग एक वर्ग बनाने के लिए किया गया है, इसलिए तार की लंबाई वर्ग का परिमाप हो जाती है।
परिमाप = 60 सेमी 4 × पार्श्व = 60 सेमी 60/4 = 15 पार्श्व = 15 सेमी
(b) दिया गया
तार की लंबाई = 60 सेमी
यदि तार का उपयोग एक समकक्ष त्रिकोण (equilateral triangle) बनाने के लिए किया जाता है, तो त्रिकोण का परिमाप = तार की लंबाई
मान लें कि त्रिकोण का पार्श्व a है
a a a = 60 3a = 60 3a = 60 a = 20 सेमी
(c) दिया गया, नियमित पेंटागन (सभी पार्श्व समान)
परिमाप = 5 × पार्श्व = 60 सेमी
पार्श्व = 12 सेमी।
Q24: चित्रग्राफ (pictograph) दिखाता है कि प्रत्येक बच्चे ने कितने स्नोबॉल (snowballs) बनाए। दिए गए प्रश्नों के उत्तर देने के लिए चित्रग्राफ का उपयोग करें। (3 अंक)
(i) अल्फ्रेडो (Alfredo) ने कितने स्नोबॉल बनाए?
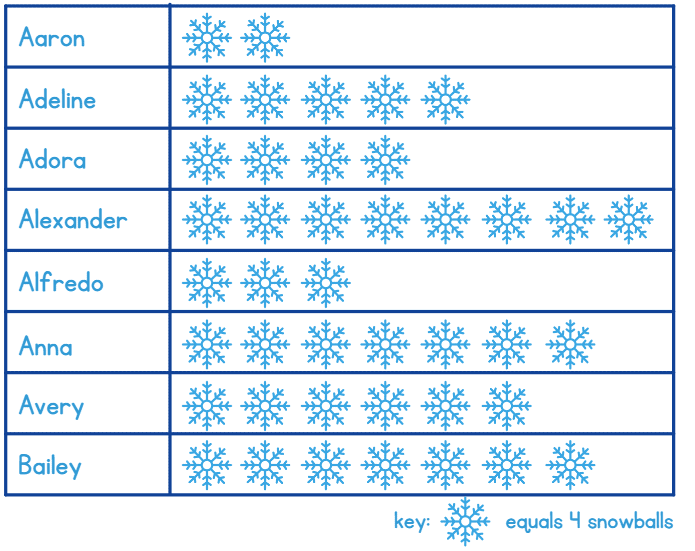
(ii) एरोन (Aaron) ने कितने स्नोबॉल बनाए?
(iii) दो ऐसे लोगों का नाम बताइए जिन्होंने समान संख्या में स्नोबॉल बनाए।
उत्तर: (i) अल्फ्रेडो के सामने 3 चित्र हैं। 1 स्नोफ्लेक (snowflake) 4 स्नोबॉल बनाए गए का प्रतिनिधित्व करता है। इसलिए, अल्फ्रेडो ने 3x4 = 12 स्नोबॉल बनाए।
(ii) एरोन के सामने 2 चित्र हैं। 1 स्नोफ्लेक 4 स्नोबॉल का प्रतिनिधित्व करता है। इसलिए, एरोन ने 2x4 = 8 स्नोबॉल बनाए।
(iii) अन्ना (Anna) और बेली (Bailey) ने समान संख्या में स्नोबॉल बनाए। हम प्रत्येक नाम के सामने स्नोफ्लेक की संख्या देख सकते हैं और देख सकते हैं कि अन्ना और बेली के नाम के सामने समान संख्या में स्नोफ्लेक बने हैं। 7 स्नोफ्लेक हैं, जिसका अर्थ है 7x4 = 28। इसलिए, अन्ना और बेली दोनों ने 28 स्नोबॉल बनाए।
Q25: दिए गए आकार का परिमाप खोजें: (3 अंक)
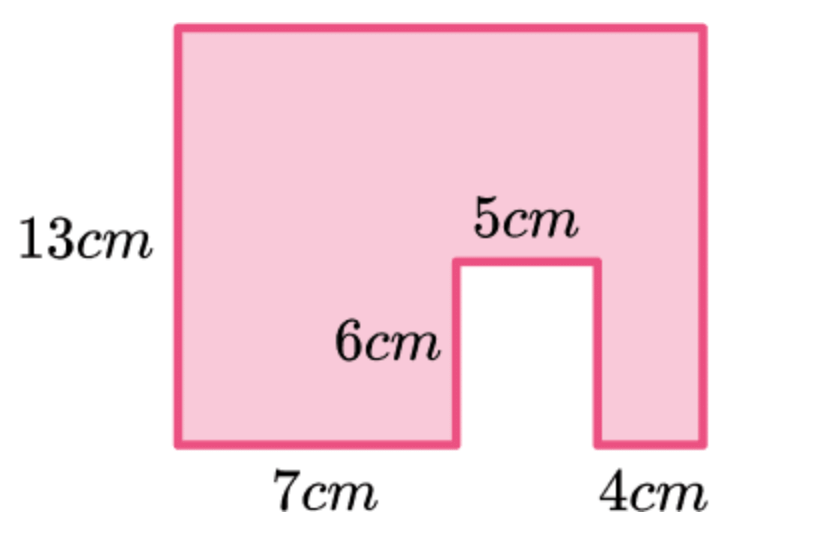
उत्तर: कुछ लंबाई गायब हैं जिन्हें हमें पहले निकालना है। हम ऊर्ध्वाधर लंबाई देख सकते हैं। गायब ऊर्ध्वाधर लंबाई 6 सेमी और 13 सेमी हैं। फिर हम गायब क्षैतिज लंबाई को देख सकते हैं। गायब पार्श्व 16 सेमी है क्योंकि 7 + 5 + 4 = 16।
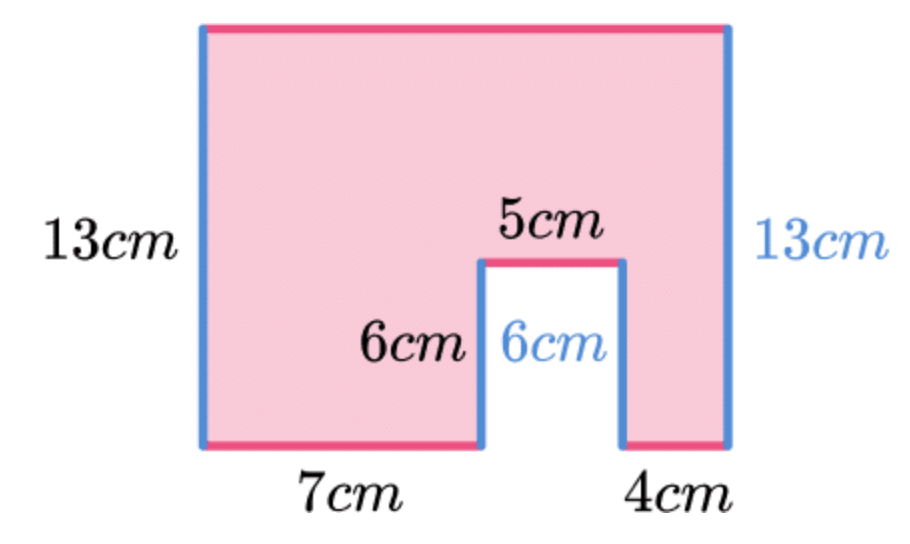
बाईं ओर से शुरू करते हुए और आकृति के चारों ओर घड़ी की दिशा में चलते हुए, हम किनारों को जोड़ सकते हैं।
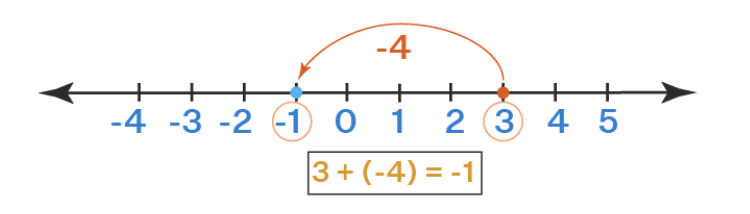
प्रश्न 26: (क) संख्या रेखा का उपयोग करके 3 (-4) का संचालन करें।
(ख) संख्या रेखा का उपयोग करके 5 - 3 का संचालन करें। (3 अंक)
(क)
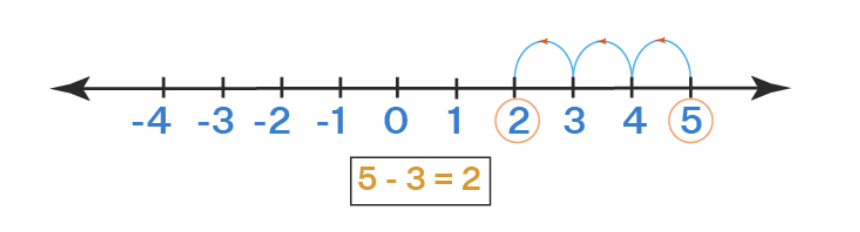
प्रश्न 27: एक आयताकार कक्षा का क्षेत्रफल 300 वर्ग मीटर है और इसकी लंबाई 25 मीटर है। कक्षा की चौड़ाई क्या होगी? (3 अंक)
उत्तर: दिया गया, कक्षा का क्षेत्रफल = 300 वर्ग मीटर लंबाई = 25 मीटर आयत का क्षेत्रफल = लंबाई × चौड़ाई ⇒ 300 = 25 × चौड़ाई ⇒ चौड़ाई = 12 मीटर
प्रश्न 28: क्या आप पैटर्न को ढूंढ सकते हैं और गायब संख्याओं को भर सकते हैं? अपने उत्तर को सही ठहराएँ। (3 अंक)

उत्तर: अनुक्रम का अवलोकन करते हुए:
- 16 → 20 (4)
- 20 → 24 (4)
- 24 → 28 (4)
पैटर्न जारी रखें:
- 28 + 4 = 32
- 32 + 4 = 36
- 36 + 4 = 40

प्रश्न 29: एक आयताकार बाग़ 120 मीटर लंबा और 80 मीटर चौड़ा है। यदि बाड़ लगाने की लागत ₹10 प्रति मीटर है, तो बाग़ को बाड़ लगाने की कुल लागत क्या होगी? (3 अंक)
उत्तर: आयत का परिमाप = 2 × (लंबाई + चौड़ाई) = 2 × (120 + 80) = 2 × 200 = 400 मीटर
कुल लागत = 400 × 10 = ₹4,000
प्रश्न 30: मान लीजिए कि आप अपने बैंक खाते में ₹0 से शुरू करते हैं, और फिर आपके पास ₹20, ₹35, और ₹45 की क्रेडिट हैं, और ₹25, ₹40, और ₹50 की डेबिट हैं। अब आपका बैंक खाता बैलेंस क्या है? (3 अंक)
उत्तर: यहाँ, क्रेडिट = ₹20 + ₹35 + ₹45 = ₹100 और डेबिट = ₹25 + ₹40 + ₹50 = ₹115
∴ बैलेंस = क्रेडिट – डेबिट = ₹100 – ₹115 = – ₹15
इसलिए, आपका बैंक खाता बैलेंस – ₹15 है।
प्रश्न 31: एक शॉपिंग मॉल में लिफ्ट ग्राउंड फ्लोर (0) से शुरू होती है। (5 अंक)
उदाहरण: यह 9 मंजिलों तक जाता है। यह अब किस मंजिल पर है?
- फिर, यह 5 मंजिल नीचे जाता है। यह अब कहाँ है?
- उसके बाद, यह 6 और मंजिल ऊपर जाता है। यह किस मंजिल पर पहुँचता है?
- अंत में, यह 10 मंजिल नीचे जाता है। लिफ्ट अब कहाँ है?
उत्तर:
- 9 मंजिल ऊपर जाने के बाद: 0 + 9 = 9, लिफ्ट 9वीं मंजिल पर है।
- 5 मंजिल नीचे जाने के बाद: 9 - 5 = 4, लिफ्ट 4वीं मंजिल पर है।
- 6 और मंजिल ऊपर जाने के बाद: 4 + 6 = 10, लिफ्ट 10वीं मंजिल पर है।
- 10 मंजिल नीचे जाने के बाद: 10 - 10 = 0, लिफ्ट फिर से ग्राउंड फ्लोर (0) पर है।
प्रश्न 32: चित्रग्राफ प्रश्न पढ़ें और उत्तर दें (5 अंक)
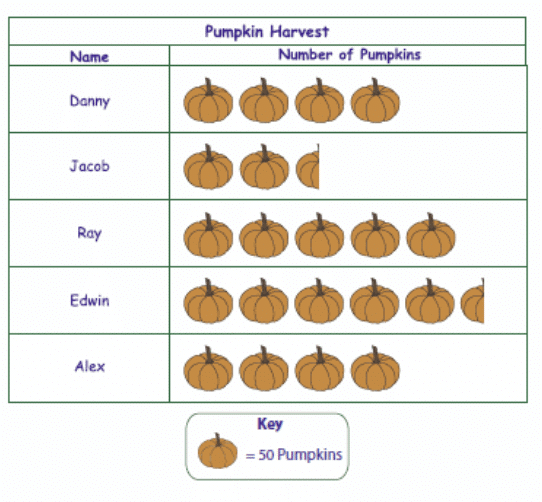
(i) सबसे अधिक किसने फसल काटी? (ii) जैकोब ने कितने कद्दू काटे? (iii) किसने 200 कद्दू काटे? (iv) उन किसानों के नाम बताएं जिन्होंने समान संख्या में कद्दू काटे? (v) डैनी ने कितने कद्दू काटे?
उत्तर: (i) एडविन (ii) 125 कद्दू (iii) डैनी और एलेक्स (iv) डैनी और एलेक्स (v) 200 कद्दू















