लाभ, हानि और छूट: हल किए गए उदाहरण | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
प्रश्न 1: अल्फोंसो, अपनी मृत्यु शय्या पर, अपनी संपत्ति का आधा हिस्सा अपनी पत्नी के लिए रखता है और बाकी को अपने तीन बेटों: बेन, कार्ल और डेव के बीच समान रूप से बांटता है। कुछ वर्षों बाद, बेन की मृत्यु हो जाती है और वह अपनी संपत्ति का आधा हिस्सा अपनी विधवा के लिए और आधा हिस्सा अपने भाइयों कार्ल और डेव के बीच समान रूप से बांटता है। जब कार्ल अपनी वसीयत बनाता है, तो वह अपनी संपत्ति का आधा हिस्सा अपनी विधवा के लिए रखता है और बाकी अपने छोटे भाई डेव को विरासत में देता है। जब कुछ वर्षों बाद डेव की मृत्यु होती है, तो वह अपनी संपत्ति का आधा हिस्सा अपनी विधवा के लिए रखता है और बाकी अपनी माँ के लिए। माँ के पास अब ₹1,575,000 हैं। कुल संपत्ति का मूल्य क्या था? (क) ₹30 लाख (ख) ₹8 लाख (ग) ₹18 लाख (घ) ₹24 लाख
सही उत्तर विकल्प (घ) है।
- कुल संपत्ति को मान लें कि अल्फोंसो की संपत्ति ₹x है। अल्फोंसो की मृत्यु के बाद, परिवार के सदस्यों के पास पैसे होंगे:
- पत्नी = x/2,
- बेन = x/6,
- कार्ल = x/6,
- डेव = x/6।
बेन की मृत्यु के बाद, उनके पास पैसे होंगे:
- अल्फोंसो की पत्नी = x/2,
- बेन = 0,
- बेन की पत्नी = x/6,
- कार्ल = x/6 x/24 = 5x/24,
- डेव = x/6 x/24 = 5x/24।
कार्ल की मृत्यु के बाद, उनके पास पैसे होंगे:
- अल्फोंसो की पत्नी के पास x/2 है,
- बेन के पास 0 है,
- बेन की पत्नी के पास x/12 है,
- कार्ल के पास 0 है,
- कार्ल की पत्नी के पास 5x/48 है,
- डेव के पास 5x/24 है।
अब, 5x/48 = 15x/48।
डेव की मृत्यु के बाद, उनके पास पैसे होंगे:
- अल्फोंसो की पत्नी के पास x/2 है,
- 15x/96 = 63x/96,
- बेन के पास 0 है,
- बेन की पत्नी के पास x/12 है,
- कार्ल के पास 0 है,
- कार्ल की पत्नी के पास 5x/48 है,
- डेव के पास 0 है और डेव की पत्नी के पास 15x/96 है।
अब, यह दिया गया है कि 63x/96 = 1575000, इसलिए x = 2400000।
वैकल्पिक विधि:

प्रश्न 1: आप इस प्रश्न को विकल्पों का उपयोग करके भी हल कर सकते हैं। यदि हम कुल राशि को Rs 2400000 मानते हैं, तो अल्फोंसो की मृत्यु के बाद परिवार के सदस्यों के पास पैसा होगा:
- अल्फोंसो की पत्नी = 1200000
- बेन = कार्ल = डेव = 400000
- बेन कार्ल और डेव के लिए 100000 छोड़ देगा।
- तो, कार्ल और डेव के पास 50000 प्रत्येक है।
- कार्ल डेव के लिए 250000 छोड़ देगा, इसलिए डेव के पास 750000 है।
- डेव ने अपनी माँ के लिए 750000/2 = 375000 छोड़ा, तो उसकी माँ के पास 1200000 - 375000 = 1575000 है, जो प्रश्न में दिया गया है। इसलिए विकल्प 4 उत्तर है।
प्रश्न 2: दो संतरे, तीन केले और चार सेब की कीमत Rs. 15 है। तीन संतरे, दो केले और एक सेब की कीमत Rs. 10 है। मैंने 3 संतरे, 3 केले और 3 सेब खरीदे। मैंने कितना भुगतान किया? (क) Rs. 10 (ख) Rs. 8 (ग) Rs. 15 (घ) निर्धारित नहीं किया जा सकता
सही उत्तर विकल्प (ग) है।
- यह दिया गया है कि 2O + 3B + 4A = 15 …..(1)
- 3O + 2B + A = 10…….(2)
- इस प्रश्न का उत्तर निर्धारित नहीं किया जा सकता क्योंकि हमें तीन चर दिए गए हैं लेकिन हम केवल दो समीकरण बना सकते हैं। लेकिन प्रश्न 3 संतरे, 3 केले और 3 सेब की व्यक्तिगत कीमत के बारे में नहीं पूछ रहा है, बल्कि यह 3O + 3B + 3A की लागत पूछता है।
- इसके लिए, यदि हम दोनों समीकरणों को जोड़ते हैं, तो हमें मिलती है: 5O + 5B + 5A = 25, O + B + A = 5।
- इसलिए 3O + 3B + 3A = 3×5 = 15।
प्रश्न 3: एक घड़ी विक्रेता प्रत्येक घड़ी बनाने के लिए Rs. 150 का खर्च उठाता है। वह 30,000 रुपये का अतिरिक्त खर्च भी उठाता है, जो बनाई गई घड़ियों की संख्या पर निर्भर नहीं करता। यदि वह सीज़न के दौरान एक घड़ी बेचने में सक्षम है, तो वह इसे Rs. 250 में बेचता है। यदि वह ऐसा करने में विफल रहता है, तो उसे प्रत्येक घड़ी Rs. 100 में बेचनी होती है। यदि वह 1500 घड़ियाँ बनाता है, तो उसे संतुलन बनाने के लिए सीज़न के दौरान कितनी घड़ियाँ बेचनी चाहिए, यह मानते हुए कि वह सभी बनाई गई घड़ियों को बेच सकता है? (क) 500 (ख) 700 (ग) 800 (घ) 1000
सही उत्तर विकल्प (b) है।
- 1500 घड़ियाँ बनाने की कुल लागत = (1500 × 150 + 30000) = रुपये 2,55,000
- मान लें कि वह सीजन के दौरान x घड़ियाँ बेचता है, इसलिए सीजन के बाद बेची गई घड़ियों की संख्या = (1500 – x)
- ∴ 1500 घड़ियों की बिक्री पर अर्जित राजस्व = 250 × x + (1500 – x) × 100 = 150x + 150000
- अब, ब्रेक-ईवन तब प्राप्त होता है जब उत्पादन लागत विक्रय मूल्य के बराबर हो। ∴ 150x + 150000 = 2,55,000 ⇒ x = 700
प्रश्न 4: एक स्टॉकिस्ट चीनी बेचकर कुछ लाभ कमाना चाहता है। वह विभिन्न तरीकों पर विचार करता है। इनमें से कौन सा तरीका उसके लाभ को अधिकतम करेगा?
- 1. चीनी को 10% लाभ पर बेचना।
- 2. 1 किलोग्राम के बजाय 900 ग्राम का वजन उपयोग करना।
- 3. चीनी में 10% अशुद्धियाँ मिलाना और चीनी को लागत मूल्य पर बेचना।
- 4. मूल्य को 5% बढ़ाना और वजन को 5% कम करना।
(a) I या III (b) II (c) II, III और IV (d) लाभ समान हैं
- हम इस प्रश्न को सभी मामलों को एक-एक करके लेकर हल करेंगे। पहले मामले में, यह दिया गया है कि लाभ 10% है।
- दूसरे मामले के लिए, मान लें कि 1 किलोग्राम चीनी की लागत मूल्य रुपये 100 है। फिर 900 ग्राम चीनी की लागत मूल्य = (100/1000) × 900 = रुपये 90। इसलिए, मामले II में लाभ % = [{(100-90)/90} × 100] = 11.11%
- मामले III के लिए, यदि वह 10% अशुद्धता जोड़ता है तो उसकी 1 किलोग्राम की लागत मूल्य = {(100/110) × 100} = रुपये 90.90। इसलिए, मामले III में लाभ % = [{(100-90.90)/90.90} × 100] = 10.01%
- और अंतिम मामले में, यदि वह वजन को 5% कम करता है।
- 950 ग्राम की लागत मूल्य = {(100/1000) × 950} = रुपये 95 और विक्रय मूल्य = रुपये 105। इसलिए, मामले IV में लाभ % = {(105 – 95)/95} × 100 = 10.52%
- इस प्रकार, लाभ दूसरे मामले में अधिकतम है।
प्रश्न 5: एक डीलर 20% नकद छूट देता है और फिर भी 20% लाभ कमाता है जब वह एक विशेष रूप से चिपचिपे मोलभाव करने वाले को एक दर्जन में 16 वस्तुएं और देता है। उसकी वस्तुओं की लागत मूल्य से कितने प्रतिशत ऊपर सूचीबद्ध थीं?
- (a) 100% (b) 80% (c) 75% (d) 66%
सही उत्तर विकल्प (a) है।
- मान लें कि लेख की लागत मूल्य (CP) Rs. x है, चूंकि उसे 20% लाभ होता है, इसलिए बिक्री मूल्य (SP) = 1.2x। यह दिया गया है कि वह 16 लेखों को एक दर्जन के लिए बेच रहा है, इसलिए वह 16 लेखों को 12 लेखों की लागत पर बेचकर नुकसान उठाता है [नुकसान = {(16-12)/16} × 100 = 25%] ∴ उसका बिक्री मूल्य = SP × 0.75। अब SP × 0.75 = 1.2x ⇒ SP = (1.2/0.75)x = 1.6x। यह SP 20% छूट देने के बाद प्राप्त हुआ है। इसलिए, मार्कड प्राइस (MP) = (1.6/0.8)x = 2x। इसका मतलब है कि लेख को लागत मूल्य से 100% ऊपर मार्क किया गया है।
- मान लें कि लागत मूल्य = Rs 100। चूंकि लाभ 20% है, तो SP = Rs 120। यह SP = Rs 120 20% छूट देने के बाद प्राप्त हुआ है, अर्थात MP = 120/0.8 = Rs 150। अब वह 16 सामानों को एक दर्जन के लिए बेच रहा है, इसलिए इस मामले में उसका नुकसान = {(16-12)/16} × 100 = 25%। इसका मतलब है कि Rs 150 25% नुकसान के बाद प्राप्त हुए। इसलिए वास्तविक MP = 150/0.75 = Rs 200। इस प्रकार, उसने MP को लागत मूल्य से 100% ऊपर मार्क किया है।
प्रश्न: 6 यदि एक व्यापारी अपने सामान के मार्कड प्राइस पर 40% छूट देता है और इस प्रकार लागत मूल्य पर बेचता है, तो % मार्क अप क्या था? (a) 28.57% (b) 40% (c) 66.66% (d) 58.33%
- यदि व्यापारी मार्कड प्राइस पर 40% छूट देता है, तो सामान 60% मार्कड प्राइस पर बेचा जाता है। प्रश्न में आगे कहा गया है कि जब छूट 40% होती है, तो व्यापारी लागत मूल्य पर बेचता है।
- इसलिए, 40% छूट पर बेचना = मार्कड प्राइस (M) का 60% = लागत मूल्य (C) या, अर्थात, एक मार्क अप 66.66% है।
प्रश्न: 7 यदि एक व्यापारी सूची मूल्य पर 30% छूट देता है, तो उसे 16% का नुकसान होता है। यदि वह सूची मूल्य पर 10% छूट पर बेचती है, तो उसे % लाभ या % नुकसान क्या होगा? (a) 6% नुकसान (b) 0.8% लाभ (c) 6.25% नुकसान (d) 8% लाभ
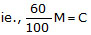
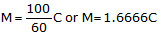
- मान लीजिए कि लेख की लागत मूल्य Rs.100 है और लेख की सूची मूल्य "x" है। तब, जब व्यापारी 30% की छूट देता है, तो व्यापारी लेख को x - 30% का x = 70% का x = 0.7x पर बेचेगा। .......(1)
- नोट: छूट को सूची मूल्य के प्रतिशत के रूप में मापा जाता है। व्यापारी द्वारा 30% की छूट देने पर जो हानि होती है, वह 16% है। इसलिए, व्यापारी को 100 - 16% का 100 = Rs.84 मिलेगा जब वह 30% की छूट देता है। .......(2)
- नोट: हानि हमेशा लागत मूल्य के प्रतिशत के रूप में मापी जाती है। इसलिए, समीकरण (1) और (2) को समान करते हुए, हमें मिलता है 0.7x = 84 या x = 120।
- यदि सूची मूल्य Rs.120 है (हमारी लागत मूल्य की धारणा Rs.100 है), तो जब व्यापारी 10% की छूट देता है, तो वह लेख को 120 - 10% का 120 = Rs.108 पर बेचेगा। जबकि लेख की लागत मूल्य Rs.100 थी और व्यापारी 10% की छूट देते समय Rs.108 प्राप्त करता है, वह 8% का लाभ कमाएगा।
प्रश्न: 8 एक व्यापारी अपने माल की कीमत को 60% बढ़ाता है और फिर मार्क की गई कीमत पर छूट देता है। यदि छूट के बाद अंतिम बिक्री मूल्य व्यापारी को न तो लाभ और न ही हानि में लाता है, तो व्यापारी द्वारा दी गई छूट का प्रतिशत क्या था? (क) 60% (ख) 40% (ग) 37.5% (घ) लागत मूल्य पर निर्भर करता है
- मान लीजिए कि लागत मूल्य 100 है। इसलिए, व्यापारी की मार्क की गई कीमत 100 + 60% का 100 = 160 होगी। अब, व्यापारी मार्क की गई कीमत पर छूट देता है। छूट का परिणाम यह है कि व्यापारी लेख को न तो लाभ और न ही हानि पर या लागत मूल्य पर बेचता है। अर्थात व्यापारी ने लेख को 100 पर बेचा है। इसलिए, दी गई छूट = 60।
- दी गई छूट आमतौर पर मार्क की गई कीमत के प्रतिशत के रूप में मापी जाती है। इसलिए, % छूट =
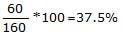
प्रश्न: 9 एक व्यापारी अपने माल की कीमत को अपने लागत मूल्य से 75% बढ़ाता है। वह अधिकतम % छूट क्या दे सकता है ताकि वह न तो लाभ और न ही हानि में बेचे? (क) 75% (ख) 46.67% (ग) 300% (घ) 42.85%
मान लीजिए कि लेख की लागत मूल्य = Rs.100
- इसलिए, व्यापारी ने इसे Rs.100 पर मार्क किया।
- 75% का Rs.100 = 100 × 0.75 = 175।
- अब, यदि वह इसे बिना लाभ या हानि के बेचता है, तो वह इसे लागत मूल्य पर बेचता है, अर्थात् वह अपने बिक्री मूल्य Rs.175 पर Rs.75 की छूट देता है।
- इसलिए, उसका % छूट = (75/175) × 100 = 42.85%
प्रश्न: 10 एक व्यापारी अपने सामान को इस प्रकार मार्क करता है कि 50 लेखों की बिक्री पर लाभ 25 लेखों की बिक्री मूल्य के बराबर होता है। उसका लाभ मार्जिन क्या है? (क) 25% (ख) 50% (ग) 100% (घ) 66.67%
- मान लीजिए कि प्रति लेख बिक्री मूल्य = Re. 1
- इसलिए, 50 लेखों का बिक्री मूल्य = Rs.50
- 50 लेखों की बिक्री पर लाभ = 25 लेखों का बिक्री मूल्य = Rs.25।
- S.P = 50। लाभ = 25। इसलिए, CP = 50 - 25 = 25।
प्रश्न: 11 दो व्यापारी प्रत्येक एक लेख को Rs.1000 में बेचते हैं। यदि व्यापारी A अपने लागत मूल्य पर लाभ की गणना करता है, जबकि व्यापारी B अपने बिक्री मूल्य पर लाभ की गणना करता है, तो वे क्रमशः 25% का लाभ प्राप्त करते हैं। व्यापारी B का लाभ व्यापारी A के लाभ से कितना अधिक है? (क) Rs.66.67 (ख) Rs.50 (ग) Rs.125 (घ) Rs.200
- व्यापारी B अपने लाभ की गणना बिक्री मूल्य के प्रतिशत के रूप में करता है। वह Rs.1000 के बिक्री मूल्य पर 25% का लाभ कमाता है। अर्थात् उसका लाभ = 25% × 1000 = Rs.250
- व्यापारी A अपने लागत मूल्य के प्रतिशत के रूप में लाभ की गणना करता है।
- इसलिए, जब वह 25% या 1/4 अपने लागत मूल्य का लाभ कमाता है, तब उसका लाभ बिक्री मूल्य के प्रतिशत के रूप में = 20% होता है।
- इसलिए, व्यापारी A Rs.1000 का 20% लाभ कमाता है = Rs.200। व्यापारी B का लाभ Rs.250 है और व्यापारी A का लाभ Rs.200 है।
- इसलिए, व्यापारी B, व्यापारी A से Rs.50 अधिक लाभ कमाता है।
प्रश्न: 12 एक साल का भुगतान सेवक को Rs. 200 और एक कमीज है। सेवक 9 महीने बाद छोड़ देता है और Rs. 120 और एक कमीज प्राप्त करता है। कमीज की कीमत क्या है? (क) Rs. 80 (ख) Rs. 100 (ग) Rs. 120 (घ) निर्धारित नहीं किया जा सकता।
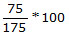
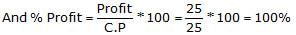
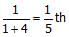
सेवक ने 12 महीनों की बजाय 9 महीनों तक काम किया, इसलिए उसे अपनी वार्षिक भुगतान का 9/12 हिस्सा प्राप्त करना चाहिए। मान लीजिए कि 1 शर्ट की कीमत Rs.S है।
- सेवक ने 12 महीनों की बजाय 9 महीनों तक काम किया, इसलिए उसे अपनी वार्षिक भुगतान का 9/12 हिस्सा प्राप्त करना चाहिए। मान लीजिए कि 1 शर्ट की कीमत Rs.S है।
- हालांकि, प्रश्न में कहा गया है कि सेवक को Rs. 120 S प्राप्त होता है, जहाँ S शर्ट की कीमत है।
- दोनों समीकरणों को समान करके हमें प्राप्त होता है = 120 S। इसलिए शर्ट की कीमत S = Rs. 120।
प्रश्न: 13 यदि सेब की दर 30 सेब के लिए एक रुपये है। तो लाभ 20% पाने के लिए कितने सेब एक रुपये में बेचे जाने चाहिए? (क) 28 (ख) 25 (ग) 20 (घ) 22
- व्यापारी 20% लाभ कमाता है। इसका मतलब है कि व्यापारी 30 सेब को Rs.1.20 में बेचता है।
- इसलिए, 1 सेब की बिक्री मूल्य = Rs. .
- Rs.1.00 में बेचे जाने वाले सेबों की संख्या = Rs. .
प्रश्न: 14 एक व्यापारी लेबल मूल्य पर 19% छूट पर सामान खरीदता है। यदि वह 10% छूट देने के बाद 20% लाभ कमाना चाहता है, तो उसका मार्कड प्राइस मूल लेबल मूल्य से कितने % अधिक होना चाहिए? (क) 8% (ख) -3.8% (ग) 33.33% (घ) इनमें से कोई नहीं
- मान लीजिए कि लेबल मूल्य = Rs.100 है। व्यापारी 19% छूट पर खरीदता है।
- इसलिए, उसकी लागत = 100 - 19 = 81।
- वह 20% लाभ कमाना चाहता है। इसलिए उसकी बिक्री मूल्य = 1.2 (81) = 97.2।
- हालांकि, वह यह Rs.97.2 10% छूट देने के बाद प्राप्त करना चाहता है। यानी, वह अपने मार्कड प्राइस के 90% पर बेचेगा।
- इसलिए, उसका मार्कड प्राइस M = = 108, जो मूल लेबल मूल्य से 8% अधिक है।
प्रश्न: 15 राजीव ने एक सामान को Rs.56 में बेचा, जिसका उसे Rs.x का खर्च आया। यदि उसे अपने खर्च पर x% लाभ होता, तो उसकी लागत क्या थी? (क) Rs.40 (ख) Rs.45 (ग) Rs.36 (घ) Rs.28
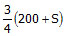
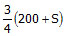
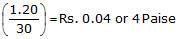
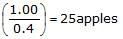
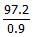
x एक लेख की लागत मूल्य है और x% लाभ का मार्जिन है। इसलिए, s.p = 56 => = 56। तो, 100x x2 = 5600। 'x' के लिए हल करते हुए, हमें x = 40 या x = -140 मिलता है। चूंकि मूल्य -ve मात्रा नहीं हो सकता है, इसलिए x = 40। लागत मूल्य 40 है और मार्कअप 40 है। आमतौर पर, ऐसे प्रश्नों को उत्तर विकल्पों से पीछे जाकर हल करना आसान होता है क्योंकि इससे काफी समय की बचत होती है।
- इसलिए, s.p = 56 => = 56। तो, 100x x2 = 5600।
प्रश्न: 16 एक व्यापारी का दावा है कि वह अपने सामान को 8% की हानि पर बेचता है लेकिन 1 किलोग्राम वजन के स्थान पर 900 ग्राम तौलता है। उसकी वास्तविक हानि या लाभ प्रतिशत क्या है? (क) 2% हानि (ख) 2.22% लाभ (ग) 2% लाभ (घ) इनमें से कोई नहीं
- व्यापारी का दावा है कि वह अपने सामान को 8% की हानि पर बेचता है। इसलिए, विक्रय मूल्य = (100 - 8)% लागत मूल्य या SP = 0.92CP।
- हालांकि, जब वह ऐसा वजन उपयोग करता है जो केवल 900 ग्राम तौलता है जबकि वह 1 किलोग्राम मापने का दावा करता है। इसलिए, CP of 900gms = 0.90 * मूल CP।
- इसलिए, वह 0.90CP का सामान 0.92CP में बेच रहा है। इसलिए, वह 0.02 CP का लाभ कमाता है अपनी 0.90 CP की लागत पर। लाभ प्रतिशत = i.e., या 2.22%।
प्रश्न: 17 एक व्यापारी दो लेख 600 रुपये में खरीदता है। वह उनमें से एक को 22% के लाभ पर और दूसरे को 8% की हानि पर बेचता है और अंत में न लाभ न हानि होती है। उस लेख का विक्रय मूल्य क्या है जिसे उसने हानि पर बेचा? (क) 404.80 रुपये (ख) 440 रुपये (ग) 536.80 रुपये (घ) 160 रुपये
- मान लीजिए कि C1 पहले लेख की लागत मूल्य है और C2 दूसरे लेख की लागत मूल्य है।
- पहले लेख को 22% के लाभ पर बेचा गया था। इसलिए, पहले लेख का विक्रय मूल्य = C1 (22/100)C1 = 1.22C1।
- दूसरे लेख को 8% की हानि पर बेचा गया। इसलिए, दूसरे लेख का विक्रय मूल्य = C2 - (8/100)C2 = 0.92C2।
- पहले और दूसरे लेख का कुल विक्रय मूल्य = 1.22C1 + 0.92C2।
- चूंकि व्यापारी ने पूरी लेनदेन में कोई लाभ या हानि नहीं की, उसके पहले और दूसरे लेख के विक्रय मूल्य की कुल लागत मूल्य के बराबर है।
- इसलिए, 1.22C1 + 0.92C2 = C1 + C2 = 600। चूंकि C1 + C2 = 600, C2 = 600 - C1।
- इसका उपयोग करते हुए 1.22C1 + 0.92C2 = 600, हम पाते हैं 1.22C1 + 0.92(600 - C1) = 600 या 1.22C1 - 0.92C1 = 600 - 0.92*600 या 0.3C1 = 0.08*600 = 48 या C1 = 48/(0.3) = 160। यदि C1 = 160, तो C2 = 600 - 160 = 440।
- जो वस्तु हानि पर बेची गई है वह लेख 2 है। लेख 2 का विक्रय मूल्य = 0.92*C2 = 0.92*440 = 404.80।
वैकल्पिक तरीका:
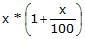
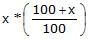
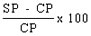
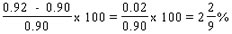
जब आप वास्तव में इस समस्या को CAT में हल करते हैं, तो आपको केवल निम्नलिखित चरणों का उपयोग करना चाहिए: 1.22C1 0.92C2 = C1 C2 = 600 1.22C1 0.92(600 - C1) = 600 C1 = 48/(0.3) = 160। C2 = 600 - 160 = 440। और उत्तर का अंतिम चरण 0.92*440 है, जिसे आपको वास्तव में गणना नहीं करनी चाहिए। चूंकि उत्तर विकल्प (b) और (c) या तो 440 या अधिक हैं, वे उत्तर नहीं हो सकते। अंतिम विकल्प 440 के 92% के लिए बहुत कम है, इसलिए उत्तर (a) होना चाहिए।
- जब आप वास्तव में इस समस्या को CAT में हल करते हैं, तो आपको केवल निम्नलिखित चरणों का उपयोग करना चाहिए: 1.22C1 0.92C2 = C1 C2 = 600 1.22C1 0.92(600 - C1) = 600 C1 = 48/(0.3) = 160। C2 = 600 - 160 = 440।
- और उत्तर का अंतिम चरण 0.92*440 है, जिसे आपको वास्तव में गणना नहीं करनी चाहिए। चूंकि उत्तर विकल्प (b) और (c) या तो 440 या अधिक हैं, वे उत्तर नहीं हो सकते।
प्रश्न: 18 एक व्यापारी को 100 लेखों को बेचने पर 75 लेखों की बिक्री मूल्य के बराबर लाभ होता है। इस लेन-देन में उसका लाभ प्रतिशत क्या है? (a) 33.33% (b) 75% (c) 300% (d) 150%
- मान लीजिए कि 1 लेख की बिक्री मूल्य S है। इसलिए, 100 लेखों की बिक्री मूल्य = 100 S। --(1)
- इन 100 लेखों को बेचने पर लाभ = 75 लेखों की बिक्री मूल्य = 75 S -- (2)
- हम जानते हैं कि बिक्री मूल्य (S.P.) = लागत मूल्य (C.P) + लाभ -- (3)
- 100 लेखों की बिक्री मूल्य = 100 S और लाभ = 75 S (1) और (2) से। इसको समीकरण (3) में प्रतिस्थापित करते हैं, तो हमें मिलता है 100 S = C.P + 75 S। इसलिए, C.P = 100 S - 75 S = 25 S। लाभ % =
- सामान्यतः, आपको इस प्रकार की समस्या को हल करने में लगभग 25 से 30 सेकंड लेना चाहिए। वास्तव में, आपको उन सभी चरणों को नहीं लिखना चाहिए जिन्हें मैंने समाधान समझाने के लिए उपयोग किया है। आपको सीधे समीकरण (c) को फ्रेम करना चाहिए और अंतिम चरण की गणना करनी चाहिए। बाकी के चरण प्रश्न को पहली बार पढ़ने के दौरान मानसिक रूप से किए जाने चाहिए।
प्रश्न: 19 यदि एक व्यापारी 20% छूट देने के बाद 20% लाभ कमाता है, तो उसे अपना मार्क-अप कितना होना चाहिए? (a) 20% (b) 40% (c) 50% (d) 60% (e) 48%
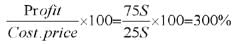
प्रश्न: 20 एक उत्पाद की अधिकतम खुदरा कीमत (MRP) इसके निर्माण लागत से 55% अधिक है। यह उत्पाद एक रिटेलर के माध्यम से बेचा जाता है, जो अपनी खरीद मूल्य पर 23% लाभ कमाता है। रिटेलर MRP पर 10% छूट देता है। निर्माता द्वारा रिटेलर को बेचे गए उत्पाद के लिए लाभ प्रतिशत (निकटतम पूर्णांक में व्यक्त) क्या है? (क) 31% (ख) 22% (ग) 15% (घ) 13% (ङ) 11%
मुख्य आंकड़े
- उत्पाद की MRP इसकी निर्माण लागत से 55% अधिक है।
- रिटेलर MRP पर 10% की छूट देने के बाद उत्पाद को बेचता है।
- रिटेलर अपनी खरीद मूल्य पर 23% लाभ कमाता है।
उपयोगी अनुमान
- लाभ हानि प्रश्नों में जहां सभी आंकड़े प्रतिशत में दिए गए हैं, लागत मूल्य को 100 मान लें। मान लें कि निर्माण लागत = 100।
- उत्पाद की MRP निर्माण लागत से 55% अधिक है। इसलिए, उत्पाद की MRP = 100 + 55% का 100 = 155।
- रिटेलर MRP पर 10% की छूट देने के बाद उत्पाद को बेचता है। तो, रिटेलर उत्पाद को 155 – 10% का 155 = 155 – 15.5 = 139.5 पर बेचता है।
- रिटेलर अपनी खरीद मूल्य पर 23% लाभ कमाता है। मान लें कि रिटेलर के लिए खरीद मूल्य x है।
- तो, रिटेलर उत्पाद को x + 23% का x = 123% का x पर बेचता है।
- रिटेलर उत्पाद को 139.5 पर बेचता है = 123% का x, यानी 1.23x = 139.5 (या) x = 139.5/1.23।
- इसलिए, x = 113.4, x रिटेलर के लिए खरीद मूल्य है।
- तो, x को निर्माता के लिए बिक्री मूल्य होना चाहिए।
- निर्माता ने उत्पाद को 113.4 पर बेचा। निर्मात्री की लागत 100 है।
- इसलिए, निर्माता द्वारा किया गया लाभ 13.4 है। चूंकि हमने लागत मूल्य को 100 मान लिया, इसलिए निर्माता 13.4% लाभ कमाता है। निकटतम पूर्णांक में, यह 13% है।
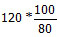
|
142 videos|172 docs|185 tests
|















