गणित में पैटर्न Chapter Notes | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

गणित क्या है?

गणित मुख्यतः पैटर्न की पहचान करने और उनके पीछे के कारणों को समझने के बारे में है। ये पैटर्न केवल पाठ्यपुस्तकों तक सीमित नहीं होते; ये हमारे चारों ओर पाए जाते हैं—प्राकृतिक संसार में, रोज़मर्रा की गतिविधियों जैसे खाना बनाना या खेल खेलना, और यहां तक कि ग्रहों के आकाश में चलने के तरीके में भी।

उदाहरण के लिए, सप्ताह एक पैटर्न का पालन करता है: सोमवार, मंगलवार, बुधवार, गुरुवार, शुक्रवार, शनिवार, रविवार। रविवार के बाद, पैटर्न फिर से सोमवार से शुरू होता है। सप्ताह के दिन पैटर्न बनाते हैं

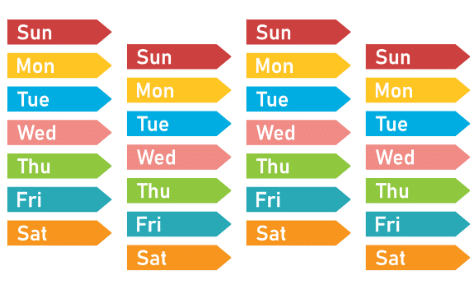
गणितज्ञ अक्सर गणित का वर्णन एक कला और विज्ञान दोनों के रूप में करते हैं, क्योंकि इन पैटर्नों को खोजने और समझाने के लिए रचनात्मकता और तार्किक सोच की आवश्यकता होती है।

यह याद रखना महत्वपूर्ण है कि गणित केवल पैटर्न की पहचान पर ध्यान केंद्रित नहीं करता; यह उन्हें समझाने का भी प्रयास करता है। ये व्याख्याएँ अक्सर उन स्थितियों से परे विभिन्न तरीकों से लागू की जा सकती हैं जिनमें इन्हें पहली बार खोजा गया था, जो समाज के लिए लाभकारी प्रगति में योगदान करती हैं।

संख्याओं में पैटर्न

संख्याओं के पैटर्न गणित के सबसे सरल और दिलचस्प हिस्सों में से एक हैं। कल्पना करें कि आप गिनते हैं: 0, 1, 2, 3, 4… यह पूर्ण संख्याओं का एक बुनियादी पैटर्न है। इन संख्याओं के पैटर्न के अध्ययन को संख्या सिद्धांत कहा जाता है।

कुछ सामान्य संख्या अनुक्रमों में शामिल हैं:

इनमें से प्रत्येक अनुक्रम में एक विशिष्ट पैटर्न या नियम होता है जो अगली संख्या को निर्धारित करता है। उदाहरण के लिए, विषम संख्याओं के अनुक्रम में, अगली संख्या प्राप्त करने के लिए आप 2 जोड़ते हैं (1 + 2 = 3, 3 + 2 = 5, और इसी तरह)।

गणितज्ञ इन पैटर्नों की खोज करने में आनंद लेते हैं, विशेषकर संख्या अनुक्रमों में, जो नियम का पालन करने वाली संख्याओं की केवल क्रमबद्ध सूचियाँ होती हैं। ये अनुक्रम गणित में पाए जाने वाले सबसे रोमांचक पैटर्न में से कुछ हैं!

संख्याओं के अनुक्रम को दृश्य रूप से प्रस्तुत करना

संख्याओं के अनुक्रम को समझना अक्सर चित्रों का उपयोग करने पर आसान होता है। इन्हें दृश्य रूप से प्रस्तुत करने से हम पैटर्न को स्पष्ट रूप से देख सकते हैं। उदाहरण के लिए:

• वर्ग संख्याएँ: इन्हें बिंदुओं के रूप में एक पूर्ण चौकोर में व्यवस्थित किया जा सकता है। उदाहरण के लिए, 4 को 2x2 बिंदुओं के चौकोर के रूप में देखा जा सकता है, और 9 को 3x3 बिंदुओं के चौकोर के रूप में।
• त्रिकोणीय संख्याएँ: इन्हें बिंदुओं के रूप में एक त्रिकोण बनाते हुए दर्शाया जा सकता है। पहले कुछ त्रिकोणीय संख्याएँ 1, 3, 6, 10, और 15 हैं, जो 1, 2, 3, 4, और 5 पंक्तियों के त्रिकोण बनाती हैं।
• घन संख्याएँ: इन्हें घनों के रूप में दर्शाया जाता है, जो मिलकर घन बनाते हैं। पहले कुछ संख्याएँ 1, 8, 27, आदि हैं।

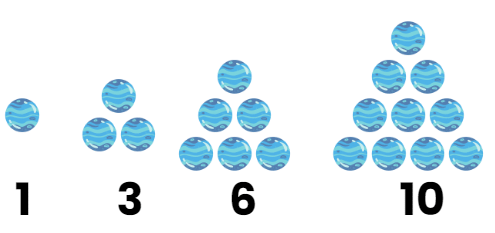
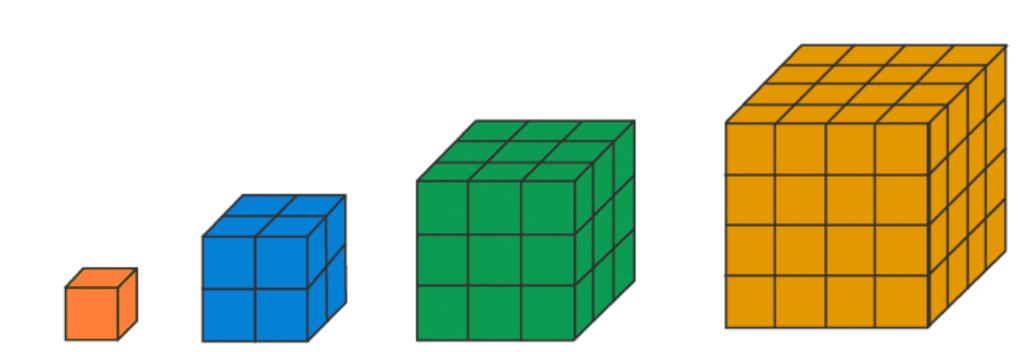
इन अनुक्रमों को दृश्य रूप से प्रस्तुत करने से हमें संख्याओं के बीच के संबंध को स्पष्ट रूप से देखने की अनुमति मिलती है। उदाहरण के लिए, 36 एक विशेष संख्या है क्योंकि यह एक वर्ग (6x6) और एक त्रिकोणीय संख्या दोनों हो सकती है।

संख्याओं के अनुक्रमों के बीच संबंध

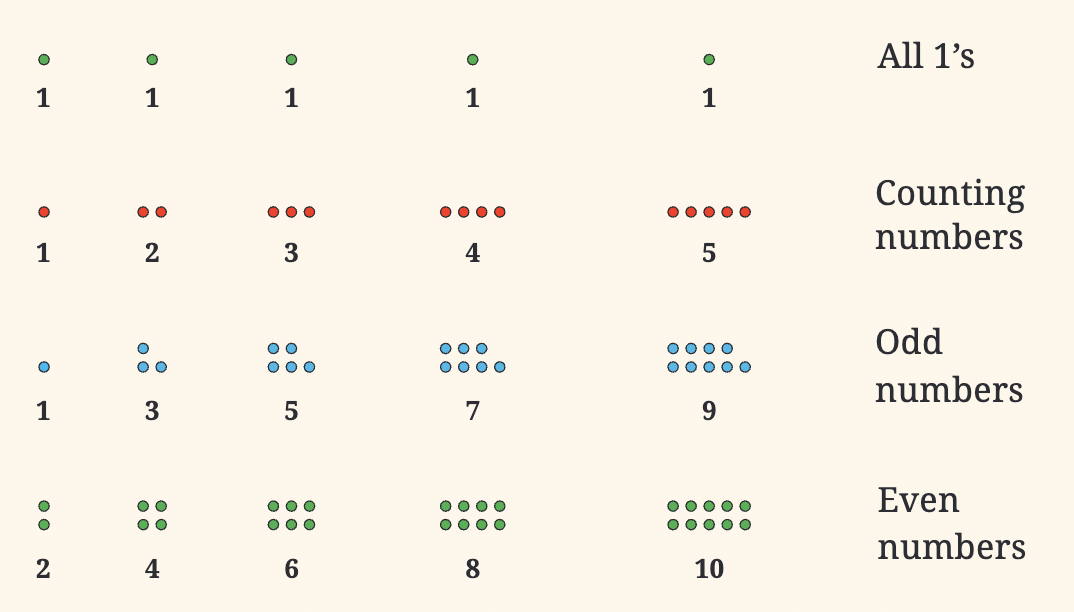
कभी-कभी, विभिन्न संख्या अनुक्रम एक-दूसरे से आश्चर्यजनक तरीकों से जुड़े होते हैं। जब आप क्रम में विषम संख्याएँ जोड़ना शुरू करते हैं, जैसे 1, 1, 3, 1, 3, 5, आदि, तो कुछ रोचक होता है: परिणाम हमेशा एक वर्ग संख्या होती है। उदाहरण के लिए:

• 1 = 1
• 1 + 3 = 4
• 1 + 3 + 5 = 9
• 1 + 3 + 5 + 7 = 16

यह पैटर्न हर बार होता है, और यह संयोग नहीं है। इसके पीछे का कारण उस चित्र में दर्शाया गया है जो आपने प्रदान किया। यह चित्र दिखाता है कि कैसे विषम संख्याओं का योग एक वर्ग आकार में बनता है।

प्रारंभिक बिंदु (1): पहला बिंदु संख्या 1 का प्रतिनिधित्व करता है।

• 3 जोड़ना: फिर, 3 बिंदुओं को जोड़कर आप एक 2x2 वर्ग बना सकते हैं।
• 5 जोड़ना: 5 और बिंदुओं को जोड़ने से एक 3x3 वर्ग बनता है।
• 7 जोड़ना: 7 बिंदुओं को जोड़ने पर एक 4x4 वर्ग बनता है।
• 9 जोड़ना: अंत में, 9 बिंदुओं को जोड़ने से एक 5x5 वर्ग बनता है।

जब आप अगला विषम संख्या जोड़ते हैं, तो यह पिछले वर्ग के चारों ओर एक परत बनाता है, जिससे एक बड़ा वर्ग बनता है। इसी कारण से पहले कुछ विषम संख्याओं का योग हमेशा एक वर्ग संख्या का परिणाम देता है। आप इसे इस तरह से दृश्य रूप में कल्पना कर सकते हैं:

पहले 10 या 100 विषम संख्याओं का योग

इस विधि का उपयोग करके, आप आसानी से दृश्य रूप में देख सकते हैं कि पहले 10 विषम संख्याओं का योग एक 10x10 वर्ग बना देगा, और पहले 100 विषम संख्याओं का योग एक 100x100 वर्ग बना देगा।

• पहले 10 विषम संख्याओं का योग: 1, 3, 5 ... 19 = 100
• पहले 100 विषम संख्याओं का योग: 1, 3, 5 ... 199 = 10,000

इस दृश्य विधि से विषम संख्याओं का योग समझना और गणना करना आसान हो जाता है, और यह दिखाता है कि ये अनुक्रम किस प्रकार वर्ग संख्याओं से संबंधित हैं।

आकृतियों में पैटर्न

गणित में, जैसे संख्याओं के साथ पैटर्न होते हैं, वैसे ही आकृतियों में भी पैटर्न होते हैं। ये पैटर्न एक, दो, या यहां तक कि तीन आयामों में मौजूद आकृतियों में पाए जाते हैं, और इन्हें ज्यामिति नामक गणित की एक शाखा में अध्ययन किया जाता है।

आकृति अनुक्रम

ज्यामिति में एक प्रमुख अवधारणा आकृति अनुक्रम की है। ये आकृतियों की क्रमबद्ध सूचियाँ होती हैं जो एक निश्चित पैटर्न या नियम का पालन करती हैं। आइए, आपके द्वारा प्रदान की गई छवि से कुछ उदाहरण देखें:

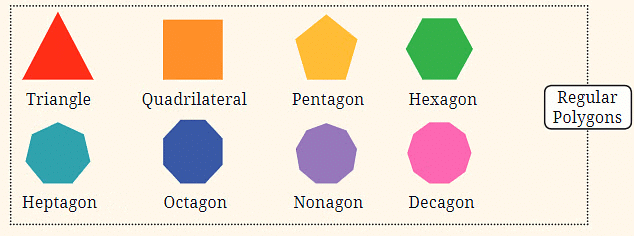
• नियमित बहुभुज: यह अनुक्रम उन बहुभुजों को दर्शाता है जिनकी भुजाएँ और कोण समान होते हैं। अनुक्रम एक त्रिकोण (3 भुजाएँ) से शुरू होता है और एक चतुर्भुज (4 भुजाएँ) में जाता है, फिर एक पंचभुज (5 भुजाएँ) में, और इसी तरह। अनुक्रम में हर कदम में आकार में एक और भुजा जोड़ी जाती है।

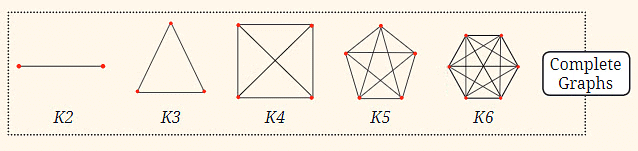
• पूर्ण ग्राफ़: ये ग्राफ़ का अनुक्रम हैं (जो रेखाओं द्वारा जुड़े बिंदुओं का संग्रह है) जहाँ प्रत्येक बिंदु हर अन्य बिंदु से जुड़ा होता है। अनुक्रम दो बिंदुओं से शुरू होता है जो एक रेखा द्वारा जुड़े होते हैं, फिर तीन बिंदुओं से एक त्रिकोण बनता है, चार बिंदुओं से एक वर्ग बनता है जिसमें विकर्ण होते हैं, और इसी तरह। जैसे-जैसे अनुक्रम आगे बढ़ता है, कनेक्शनों की संख्या बढ़ती है।

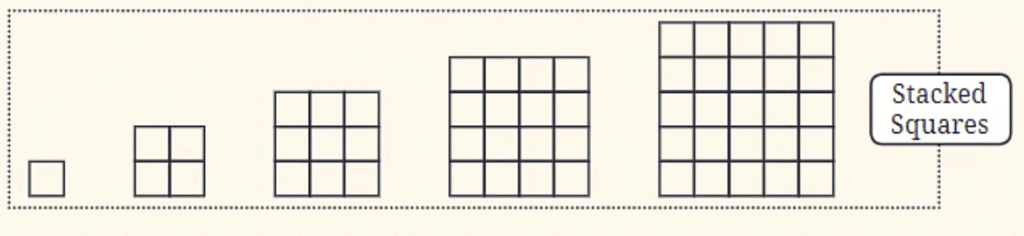
• स्टैक्ड वर्ग: यह अनुक्रम उन वर्गों को दर्शाता है जो एक-दूसरे के ऊपर रखे जाते हैं, एकल वर्ग से शुरू होकर छोटे वर्गों से बना एक बड़े वर्ग में बढ़ता है। जैसे-जैसे आप अनुक्रम के साथ बढ़ते हैं, वर्गों की कुल संख्या एक ग्रिड पैटर्न में बढ़ती है।

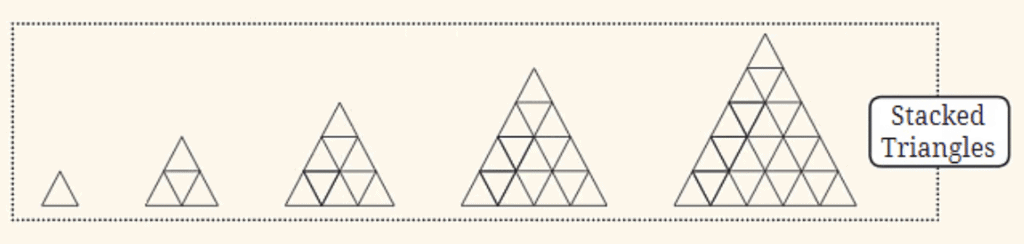
• स्टैक्ड त्रिकोण: स्टैक्ड वर्गों के समान, यह अनुक्रम त्रिकोणों को एक बड़े त्रिकोण बनाने के लिए ढेर करता है। अनुक्रम एक एकल त्रिकोण से शुरू होता है और छोटे त्रिकोणों की अधिक पंक्तियाँ जोड़कर एक बड़े त्रिकोण का निर्माण करता है।

• कोच स्नोफ्लेक: यह एक प्रसिद्ध फ्रैक्टल आकार है जो एक सरल त्रिकोण से शुरू होता है। अनुक्रम के प्रत्येक चरण में, प्रत्येक भुजा पर छोटे त्रिकोण जोड़े जाते हैं, जिससे एक अधिक जटिल पैटर्न बनता है जो एक स्नोफ्लेक के समान होता है।

ये आकार अनुक्रम उदाहरण हैं कि पैटर्न केवल संख्याओं में ही नहीं बल्कि आकार की ज्यामिति में भी पाए जा सकते हैं।

संख्यात्मक अनुक्रमों के साथ संबंध

आकृतियों और संख्याओं के अनुक्रम अक्सर दिलचस्प तरीकों से जुड़े होते हैं। इन संबंधों को समझने से दोनों प्रकार के अनुक्रमों का अध्ययन करना आसान हो सकता है।

उदाहरण: नियमित बहुभुज और गणना करने वाली संख्याएँ

आइए नियमित बहुभुजों के आकृति अनुक्रम से शुरू करते हैं। इस अनुक्रम में, प्रत्येक आकृति को इसके किनारों की संख्या द्वारा परिभाषित किया गया है। अनुक्रम इस प्रकार शुरू होता है:

• एक त्रिभुज (3 किनारे)
• एक चतुष्कोण (4 किनारे)
• एक पंचकोण (5 किनारे)
• आदि...

किनारों की संख्या गणना करने वाली संख्याओं से शुरू होती है: 3, 4, 5, 6, 7, 8, 9, 10, आदि। इसलिए इन आकृतियों को तदनुसार नामित किया गया है, जैसे त्रिभुज (3 किनारे), चतुष्कोण (4 किनारे), पंचकोण (5 किनारे), आदि। \"नियमित\" शब्द का अर्थ है कि सभी किनारे समान लंबाई के होते हैं और सभी कोण समान होते हैं, यानी आकृति पूरी तरह से सममित होती है।

अन्य आकृति अनुक्रमों में संबंध

अन्य आकृति अनुक्रमों में भी संख्याओं के अनुक्रमों से दिलचस्प संबंध होते हैं। उदाहरण के लिए:

• संगठित वर्ग वर्ग संख्याओं (1, 4, 9, 16, ...) से संबंधित हो सकते हैं, जहां अनुक्रम में प्रत्येक कदम एक और पंक्ति और स्तंभ जोड़ता है।
• पूर्ण ग्राफ संयोगों या किनारों की संख्या से संबंधित होते हैं, जो त्रिकोणीय संख्याओं के समान पैटर्न में बढ़ते हैं।

आइए अभ्यास करें!

प्रश्न: आप निम्नलिखित संख्याओं के अनुक्रम को क्या कहेंगे?

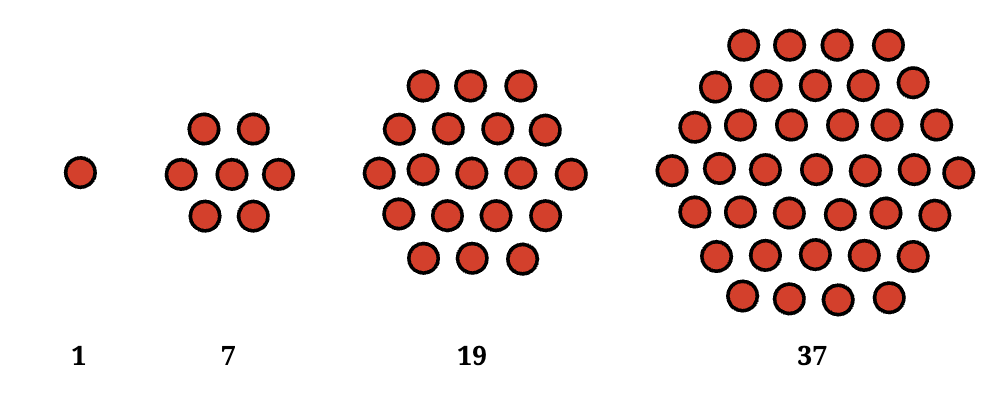
उत्तर: इन्हें हेक्सागोनल संख्याएँ कहा जाता है! हेक्सागोनल संख्याएँ विशेष संख्याएँ हैं जो हेक्सागोन के आकार में व्यवस्थित बिंदुओं का प्रतिनिधित्व करती हैं। पैटर्न एकल केंद्रीय बिंदु से शुरू होता है, और प्रत्येक नई परत इसके चारों ओर बिंदुओं की एक रिंग जोड़ती है, जिससे एक बड़ा हेक्सागोन बनता है। प्रत्येक परत में बिंदुओं की संख्या 6 से बढ़ती है, जिससे अनुक्रम बनता है जैसे 1, 7, 19, 37, आदि।

प्रश्न: क्या आप इस अनुक्रम में पैटर्न पहचान सकते हैं?

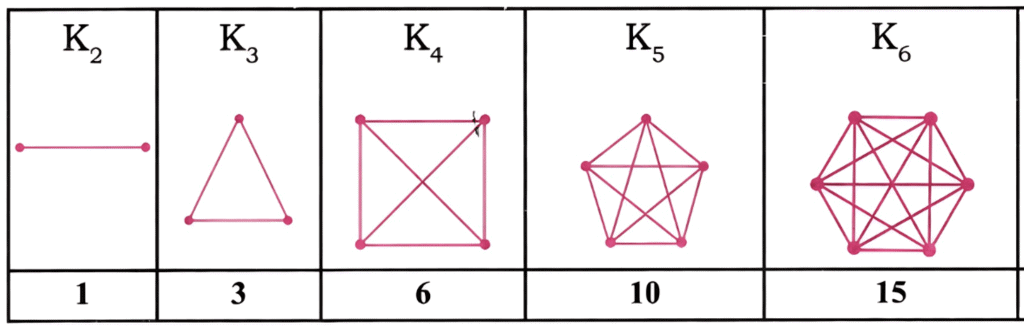
यहां रेखाओं की संख्या इस प्रकार है:

K2 = 1

K3 = 3

K4 = 6

K5 = 10

K6 = 15

इस प्रकार श्रृंखला 1, 3, 6, 10, 15,… है।

इसलिए, यह एक त्रिकोणीय संख्या अनुक्रम है।

सारांश

सारांश

• गणित को पैटर्न और उनके अस्तित्व के पीछे के तर्क का अध्ययन माना जा सकता है।
• गणित में एक मौलिक पैटर्न संख्या अनुक्रम हैं।
• संख्या अनुक्रम के प्रमुख उदाहरणों में गिनती की संख्या, विषम और सम संख्या, वर्ग संख्या, त्रिकोणीय संख्या, घन संख्या, विरहांका संख्या, और 2 के घात शामिल हैं।
• संख्या अनुक्रम अक्सर दिलचस्प संबंध रखते हैं। उदाहरण के लिए, 1 से शुरू होने वाले विषम संख्याओं के अनुक्रम का योग वर्ग संख्याओं में परिणत होता है।
• दृश्य प्रतिनिधित्व का उपयोग संख्या अनुक्रम और उनके अंतर्संबंधों को समझने में सहायता कर सकता है।
• गणितीय पैटर्न का एक और मौलिक प्रकार आकार अनुक्रम हैं।
• आकार अनुक्रम के उल्लेखनीय उदाहरणों में नियमित बहुभुज, पूर्ण ग्राफ, ढेर किए गए त्रिकोण और वर्ग, और कोच स्नोफ्लेक के पुनरावृत्तियाँ शामिल हैं।
• आकार अनुक्रम अक्सर संख्या अनुक्रम के साथ दिलचस्प संबंध प्रदर्शित करते हैं।
• आकृतियों और संख्याओं के बीच इन संबंधों को पहचानकर, आप ज्यामिति और अंकगणित दोनों में पैटर्न की गहरी समझ प्राप्त कर सकते हैं।
• इन पैटर्न और संबंधों को समझना वह बड़ा हिस्सा है जो गणित को चुनौतीपूर्ण और सुंदर बनाता है!