Sorting Algorithms | GATE Computer Science Engineering(CSE) 2026 Mock Test Series - Computer Science Engineering (CSE) PDF Download
| Table of contents |

|
| Sorting Algorithms - Introduction |

|
| Complexity of Sorting Algorithms |

|
| Selection Sort |

|
| Bubble Sort |

|
| Insertion Sort |

|
| Merge Sort |

|
| Heap Sort |

|
| QuickSort |

|
Ever thought how products are arranged when you use filters like low-to-high or high-to-low or on Amazon or any other e-commerce website? For websites with a large number of products featured, sorting algorithms are essential to make it easier for users to view the products.
Sorting Algorithms - Introduction
A sorting algorithm is an algorithm made up of a series of instructions that takes an array as input, performs specified operations on the array, sometimes called a list, and outputs a sorted array.
Mainly there are five basic algorithms used and you can derive multiple algorithms using these basic algorithms. Each of these algorithms has some pros and cons and can be chosen effectively depending on the size of data to be handled.
- Insertion Sort
- Selection Sort
- Bubble Sort
- Merge Sort
- Quick Sort
Complexity of Sorting Algorithms
The efficiency of any sorting algorithm is determined by the time complexity and space complexity of the algorithm.1. Time Complexity: Time complexity refers to the time taken by an algorithm to complete its execution with respect to the size of the input. It can be represented in different forms:
- Big-O notation (O)
- Omega notation (Ω)
- Theta notation (Θ)
2. Space Complexity: Space complexity refers to the total amount of memory used by the algorithm for a complete execution. It includes both the auxiliary memory and the input. The auxiliary memory is the additional space occupied by the algorithm apart from the input data.
Selection Sort
The selection sort algorithm sorts an array by repeatedly finding the minimum element (considering ascending order) from unsorted part and putting it at the beginning.
The algorithm maintains two subarrays in a given array.
1) The subarray which is already sorted.
2) Remaining subarray which is unsorted.
In every iteration of selection sort, the minimum element (considering ascending order) from the unsorted subarray is picked and moved to the sorted subarray.
Example
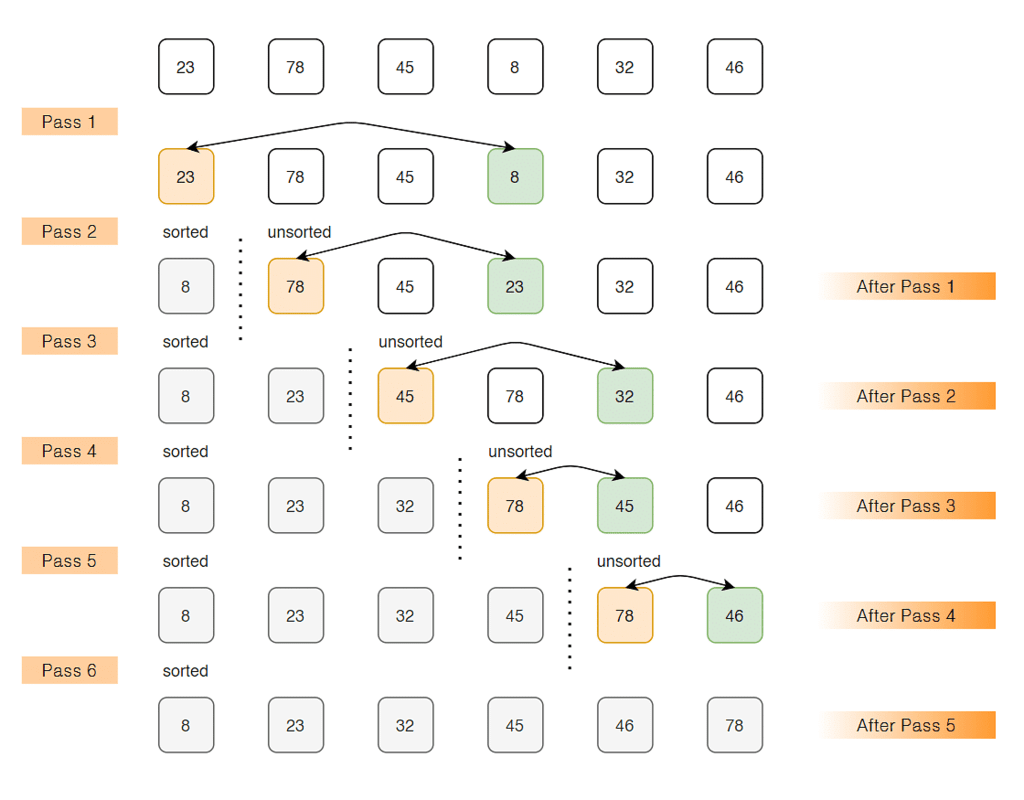
Lets consider the following array as an example: arr[] = {23, 78, 45, 8, 32, 46}
1. Find the minimum element in arr[0...5] and place it at beginning.
{8, 78, 45, 23, 32, 46}
2. Find the minimum element in arr[1...5] and place it at beginning of arr[1...5]
{8, 23, 45, 78, 32, 46}
3. Find the minimum element in arr[2...5] and place it at beginning of arr[2...5]
{8, 23, 32, 78, 45, 46}
4. Find the minimum element in arr[3...5] and place it at beginning of arr[3...5]
{8, 23, 32, 45, 78, 46}
5. Find the minimum element in arr[4...5] and place it at beginning of arr[4...5]
{8, 23, 32, 45, 46, 78}
C program for implementation of selection sort
#include <stdio.h>
void swap(int *xp, int *yp)
{
int temp = *xp;
*xp = *yp;
*yp = temp;
}
void selectionSort(int arr[], int n)
{
int i, j, min_idx;
// One by one move boundary of unsorted subarray
for (i = 0; i < n-1; i++)
{
// Find the minimum element in unsorted array
min_idx = i;
for (j = i+1; j < n; j++)
if (arr[j] < arr[min_idx])
min_idx = j;
// Swap the found minimum element with the first element
swap(&arr[min_idx], &arr[i]);
}
}
/* Function to print an array */
void printArray(int arr[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", arr[i]);
printf(" ");
}
// Driver program to test above functions
int main()
{
int arr[] = {23, 78, 45, 8, 32, 46};
int n = sizeof(arr)/sizeof(arr[0]);
selectionSort(arr, n);
printf("Sorted array: ");
printArray(arr, n);
return 0;
}
Output:
Sorted array: {11, 12, 22, 25, 64}
Complexity Analysis of Selection Sort:
Time Complexity: The time complexity of Selection Sort is O(N2) as there are two nested loops:
- One loop to select an element of Array one by one = O(N)
- Another loop to compare that element with every other Array element = O(N)
Therefore overall complexity = O(N) * O(N) = O(N*N) = O(N2)
Auxiliary Space: O(1) as the only extra memory used is for temporary variables while swapping two values in Array. The selection sort never makes more than O(N) swaps and can be useful when memory write is a costly operation.
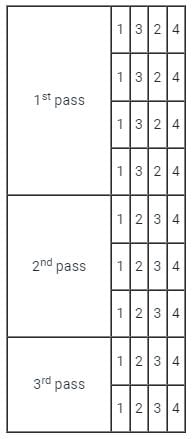
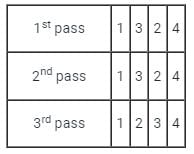
Bubble Sort
Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in wrong order.
Example:
First Pass:
( 5 1 4 2 8 ) –> ( 1 5 4 2 8 ), Here, algorithm compares the first two elements, and swaps since 5 > 1.
( 1 5 4 2 8 ) –> ( 1 4 5 2 8 ), Swap since 5 > 4
( 1 4 5 2 8 ) –> ( 1 4 2 5 8 ), Swap since 5 > 2
( 1 4 2 5 8 ) –> ( 1 4 2 5 8 ), Now, since these elements are already in order (8 > 5), algorithm does not swap them.
Second Pass:
( 1 4 2 5 8 ) –> ( 1 4 2 5 8 )
( 1 4 2 5 8 ) –> ( 1 2 4 5 8 ), Swap since 4 > 2
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
Now, the array is already sorted, but our algorithm does not know if it is completed. The algorithm needs one whole pass without any swap to know it is sorted.
Third Pass:
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
Following are C/C++, Python and Java implementations of Bubble Sort.
C program for implementation of Bubble sort
#include <stdio.h>
void swap(int *xp, int *yp)
{
int temp = *xp;
*xp = *yp;
*yp = temp;
}
// A function to implement bubble sort
void bubbleSort(int arr[], int n)
{
int i, j;
for (i = 0; i < n-1; i++)
// Last i elements are already in place
for (j = 0; j < n-i-1; j++)
if (arr[j] > arr[j+1])
swap(&arr[j], &arr[j+1]);
}
/* Function to print an array */
void printArray(int arr[], int size)
{
for (int i=0; i < size; i++)
printf("%d ", arr[i]);
printf(" ");
}
// Driver program to test above functions
int main()
{
int arr[] = {64, 34, 25, 12, 22, 11, 90};
int n = sizeof(arr)/sizeof(arr[0]);
bubbleSort(arr, n);
printf("Sorted array: ");
printArray(arr, n);
return 0;
}
Output:
Sorted array: {11 12 22 25 34 64 90}
Illustration :
 |
Test: Sorting- 1
|
Start Test |
The Complexity of the Bubble Sort Algorithm
The Time Complexity of the Bubble Sort Algorithm
- Bubble sort employs two loops: an inner loop and an outer loop.
- The inner loop performs O(n) comparisons deterministically.
Worst Case
- In the worst-case scenario, the outer loop runs O(n) times.
- As a result, the worst-case time complexity of bubble sort is O(n x n) = O(n x n) (n2).
Best Case
- In the best-case scenario, the array is already sorted, but just in case, bubble sort performs O(n) comparisons.
- As a result, the time complexity of bubble sort in the best-case scenario is O(n).
Average Case
- Bubble sort may require (n/2) passes and O(n) comparisons for each pass in the average case.
- As a result, the average case time complexity of bubble sort is O(n/2 x n) = O(n/2 x n) = O(n/2 x n) = O(n/2 x n) = O (n2).
The Space Complexity of the Bubble Sort Algorithm
- Bubble sort requires only a fixed amount of extra space for the flag, i, and size variables.
- As a result, the space complexity of bubble sort is O. (1).
- It is an in-place sorting algorithm, which modifies the original array's elements to sort the given array.
Importance of Bubble Sort
Due to its simplicity, bubble sort is often used to introduce the concept of a sorting algorithm.
In computer graphics it is popular for its capability to detect a very small error (like swap of just two elements) in almost-sorted arrays and fix it with just linear complexity (2n). For example, it is used in a polygon filling algorithm, where bounding lines are sorted by their x coordinate at a specific scan line (a line parallel to x axis) and with incrementing y their order changes (two elements are swapped) only at intersections of two lines.
Insertion Sort
Insertion sort is a simple sorting algorithm that works the way we sort playing cards in our hands. The array is virtually split into a sorted and an unsorted part. Values from the unsorted part are picked and placed at the correct position in the sorted part.
Algorithm
To sort an array of size N in ascending order:
- Iterate from arr[1] to arr[N] over the array.
- Compare the current element (key) to its predecessor.
- If the key element is smaller than its predecessor, compare it to the elements before. Move the greater elements one position up to make space for the swapped element.
Example:
Another Example:
{12, 11, 13, 5, 6}
Let us loop for i = 1 (second element of the array) to 5 (Size of input array)
i = 1. Since 11 is smaller than 12, move 12 and insert 11 before 12
{11, 12, 13, 5, 6}
i = 2. 13 will remain at its position as all elements in A[0..I-1] are smaller than 13
{11, 12, 13, 5, 6}
i = 3. 5 will move to the beginning and all other elements from 11 to 13 will move one position ahead of their current position.
{5, 11, 12, 13, 6}
i = 4. 6 will move to position after 5, and elements from 11 to 13 will move one position ahead of their current position.
{5, 6, 11, 12, 13}
C program for insertion sort
#include <stdio.h>
#include <math.h>
/* Function to sort an array using insertion sort*/
void insertionSort(int arr[], int n)
{
int i, key, j;
for (i = 1; i < n; i++)
{
key = arr[i];
j = i-1;
/* Move elements of arr[0..i-1], that are
greater than key, to one position ahead
of their current position */
while (j >= 0 && arr[j] > key)
{
arr[j+1] = arr[j];
j = j-1;
}
arr[j+1] = key;
}
}
// A utility function ot print an array of size n
void printArray(int arr[], int n)
{
int i;
for (i=0; i < n; i++)
printf("%d ", arr[i]);
printf(" ");
}
/* Driver program to test insertion sort */
int main()
{
int arr[] = {12, 11, 13, 5, 6};
int n = sizeof(arr)/sizeof(arr[0]);
insertionSort(arr, n);
printArray(arr, n);
return 0;
}
Output:
5 6 11 12 13
Time Complexity: O(n*n)
Auxiliary Space: O(1)
Boundary Cases: Insertion sort takes maximum time to sort if elements are sorted in reverse order. And it takes minimum time (Order of n) when elements are already sorted.
Algorithmic Paradigm: Incremental Approach
Sorting In Place: Yes
Stable: Yes
Online: Yes
Uses: Insertion sort is used when number of elements is small. It can also be useful when input array is almost sorted, only few elements are misplaced in complete big array.
What is Binary Insertion Sort?
We can use binary search to reduce the number of comparisons in normal insertion sort. Binary Insertion Sort find use binary search to find the proper location to insert the selected item at each iteration. In normal insertion, sort it takes O(i) (at ith iteration) in worst case. we can reduce it to O(logi) by using binary search. The algorithm as a whole still has a running worst case running time of O(n2) because of the series of swaps required for each insertion.
How to implement Insertion Sort for Linked List?
Below is simple insertion sort algorithm for linked list.
1) Create an empty sorted (or result) list
2) Traverse the given list, do following for every node.
......a) Insert current node in sorted way in sorted or result list.
3) Change head of given linked list to head of sorted (or result) list.
Merge Sort
Like QuickSort, Merge Sort is a Divide and Conquer algorithm. It divides input array in two halves, calls itself for the two halves and then merges the two sorted halves.
The merge() function is used for merging two halves. The merge(arr, l, m, r) is key process that assumes that arr[l..m] and arr[m+1..r] are sorted and merges the two sorted sub-arrays into one.
C implementation for Merge Sort
MergeSort(arr[], l, r)
If r > l
1. Find the middle point to divide the array into two halves:
middle m = (l+r)/2
2. Call mergeSort for first half:
Call mergeSort(arr, l, m)
3. Call mergeSort for second half:
Call mergeSort(arr, m+1, r)
4. Merge the two halves sorted in step 2 and 3:
Call merge(arr, l, m, r)
The following diagram shows the complete merge sort process for an example array {38, 27, 43, 3, 9, 82, 10}. If we take a closer look at the diagram, we can see that the array is recursively divided in two halves till the size becomes 1. Once the size becomes 1, the merge processes comes into action and starts merging arrays back till the complete array is merged.
C program for Merge Sort
#include<stdlib.h>
#include<stdio.h>
// Merges two subarrays of arr[].
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
void merge(int arr[], int l, int m, int r)
{
int i, j, k;
int n1 = m - l + 1;
int n2 = r - m;
/* create temp arrays */
int L[n1], R[n2];
/* Copy data to temp arrays L[] and R[] */
for (i = 0; i < n1; i++)
L[i] = arr[l + i];
for (j = 0; j < n2; j++)
R[j] = arr[m + 1+ j];
/* Merge the temp arrays back into arr[l..r]*/
i = 0; // Initial index of first subarray
j = 0; // Initial index of second subarray
k = l; // Initial index of merged subarray
while (i < n1 && j < n2)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
/* Copy the remaining elements of L[], if there
are any */
while (i < n1)
{
arr[k] = L[i];
i++;
k++;
}
/* Copy the remaining elements of R[], if there
are any */
while (j < n2)
{
arr[k] = R[j];
j++;
k++;
}
}
/* l is for left index and r is right index of the
sub-array of arr to be sorted */
void mergeSort(int arr[], int l, int r)
{
if (l < r)
{
// Same as (l+r)/2, but avoids overflow for
// large l and h
int m = l+(r-l)/2;
// Sort first and second halves
mergeSort(arr, l, m);
mergeSort(arr, m+1, r);
merge(arr, l, m, r);
}
}
/* UTILITY FUNCTIONS */
/* Function to print an array */
void printArray(int A[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", A[i]);
printf(" ");
}
/* Driver program to test above functions */
int main()
{
int arr[] = {12, 11, 13, 5, 6, 7};
int arr_size = sizeof(arr)/sizeof(arr[0]);
printf("Given array is ");
printArray(arr, arr_size);
mergeSort(arr, 0, arr_size - 1);
printf(" Sorted array is ");
printArray(arr, arr_size);
return 0;
}
Output:
Given array is: {12 11 13 5 6 7}
Sorted array is: {5 6 7 11 12 13}
Time Complexity: Sorting arrays on different machines. Merge Sort is a recursive algorithm and time complexity can be expressed as following recurrence relation.
T(n) = 2T(n/2) +
The above recurrence can be solved either using Recurrence Tree method or Master method. It falls in case II of Master Method and solution of the recurrence is
Time complexity of Merge Sort is in all 3 cases (worst, average and best) as merge sort always divides the array in two halves and take linear time to merge two halves.
Auxiliary Space: O(n)
Algorithmic Paradigm: Divide and Conquer
Sorting In Place: No in a typical implementation
Stable: Yes
Applications of Merge Sort
- Merge Sort is useful for Sorting linked lists in O(nlogn) time.In case of linked lists the case is different mainly due to difference in memory allocation of arrays and linked lists. Unlike arrays, linked list nodes may not be adjacent in memory. Unlike array, in linked list, we can insert items in the middle in O(1) extra space and O(1) time. Therefore merge operation of merge sort can be implemented without extra space for linked lists.
- In arrays, we can do random access as elements are continuous in memory. Let us say we have an integer (4-byte) array A and let the address of A[0] be x then to access A[i], we can directly access the memory at (x + i*4). Unlike arrays, we can not do random access in linked list. Quick Sort requires a lot of this kind of access. In linked list to access i’th index, we have to travel each and every node from the head to i’th node as we don’t have continuous block of memory. Therefore, the overhead increases for quick sort. Merge sort accesses data sequentially and the need of random access is low.
 |
Download the notes
Sorting Algorithms
|
Download as PDF |
Heap Sort
Heap sort is a comparison based sorting technique based on Binary Heap data structure. It is similar to selection sort where we first find the maximum element and place the maximum element at the end.
We repeat the same process for remaining element.
What is Binary Heap ?
Let us first define a Complete Binary Tree. A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible
A Binary Heap is a Complete Binary Tree where items are stored in a special order such that value in a parent node is greater(or smaller) than the values in its two children nodes. The former is called as max heap and the latter is called min heap. The heap can be represented by binary tree or array.
Why array based representation for Binary Heap?
Since a Binary Heap is a Complete Binary Tree, it can be easily represented as array and array based representation is space efficient. If the parent node is stored at index I, the left child can be calculated by 2 * I + 1 and right child by 2 * I + 2 (assuming the indexing starts at 0).
Heap Sort Algorithm for sorting in increasing order:
1. Build a max heap from the input data.
2. At this point, the largest item is stored at the root of the heap. Replace it with the last item of the heap followed by reducing the size of heap by 1. Finally, heapify the root of tree.
3. Repeat above steps while size of heap is greater than 1.
How to build the heap?
Heapify procedure can be applied to a node only if its children nodes are heapified. So the heapification must be performed in the bottom up order.
Lets understand with the help of an example:
C++ program for implementation of Heap Sort
#include <iostream>using namespace std;
// To heapify a subtree rooted with node i which is
// an index in arr[]. n is size of heap
void heapify(int arr[], int n, int i)
{
int largest = i; // Initialize largest as root
int l = 2*i + 1; // left = 2*i + 1
int r = 2*i + 2; // right = 2*i + 2
// If left child is larger than root
if (l < n && arr[l] > arr[largest])
largest = l;
// If right child is larger than largest so far
if (r < n && arr[r] > arr[largest])
largest = r;
// If largest is not root
if (largest != i)
{
swap(arr[i], arr[largest]);
// Recursively heapify the affected sub-tree
heapify(arr, n, largest);
}
}
// main function to do heap sort
void heapSort(int arr[], int n)
{
// Build heap (rearrange array)
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
// One by one extract an element from heap
for (int i=n-1; i>=0; i--)
{
// Move current root to end
swap(arr[0], arr[i]);
// call max heapify on the reduced heap
heapify(arr, i, 0);
}
}
/* A utility function to print array of size n */
void printArray(int arr[], int n)
{
for (int i=0; i<n; ++i)
cout << arr[i] << " ";
cout << " ";
}
// Driver program
int main()
{
int arr[] = {12, 11, 13, 5, 6, 7};
int n = sizeof(arr)/sizeof(arr[0]);
heapSort(arr, n);
cout << "Sorted array is ";
printArray(arr, n);
}
Output:
Sorted array is: {5 6 7 11 12 13}
Notes:
Heap sort is an in-place algorithm.
Its typical implementation is not stable, but can be made stable.
Time Complexity: Time complexity of heapify is O(Logn). Time complexity of createAndBuildHeap() is O(n) and overall time complexity of Heap Sort is O(nLogn).
QuickSort
Like Merge Sort, QuickSort is a Divide and Conquer algorithm. It picks an element as pivot and partitions the given array around the picked pivot.
There are many different versions of quickSort that pick pivot in different ways.
- Always pick first element as pivot.
- Always pick last element as pivot (implemented below)
- Pick a random element as pivot.
- Pick median as pivot.
The key process in quickSort is partition(). Target of partitions is, given an array and an element x of array as pivot, put x at its correct position in sorted array and put all smaller elements (smaller than x) before x, and put all greater elements (greater than x) after x. All this should be done in linear time.
Pseudo Code for recursive QuickSort function :
/* low --> Starting index, high --> Ending index */
quickSort(arr[], low, high)
{
if (low < high)
{
/* pi is partitioning index, arr[p] is now
at right place */
pi = partition(arr, low, high);
quickSort(arr, low, pi - 1); // Before pi
quickSort(arr, pi + 1, high); // After pi
}
}
Partition Algorithm
There can be many ways to do partition, following pseudo code adopts the method given in CLRS book. The logic is simple, we start from the leftmost element and keep track of index of smaller (or equal to) elements as i. While traversing, if we find a smaller element, we swap current element with arr[i]. Otherwise we ignore current element.
/* low --> Starting index, high --> Ending index */
quickSort(arr[], low, high)
{
if (low < high)
{
/* pi is partitioning index, arr[p] is now
at right place */
pi = partition(arr, low, high);
quickSort(arr, low, pi - 1); // Before pi
quickSort(arr, pi + 1, high); // After pi
}
}
Pseudo code for partition()
/* This function takes last element as pivot, places
the pivot element at its correct position in sorted
array, and places all smaller (smaller than pivot)
to left of pivot and all greater elements to right
of pivot */
partition (arr[], low, high)
{
// pivot (Element to be placed at right position)
pivot = arr[high];
i = (low - 1) // Index of smaller element
for (j = low; j <= high- 1; j++)
{
// If current element is smaller than or
// equal to pivot
if (arr[j] <= pivot)
{
i++; // increment index of smaller element
swap arr[i] and arr[j]
}
}
swap arr[i + 1] and arr[high])
return (i + 1)
}
Illustration of partition() :
arr[] = {10, 80, 30, 90, 40, 50, 70}
Indexes: 0 1 2 3 4 5 6
low = 0, high = 6, pivot = arr[h] = 70
Initialize index of smaller element, i = -1
Traverse elements from j = low to high-1
j = 0 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 0
arr[] = {10, 80, 30, 90, 40, 50, 70} // No change as i and j
// are same
j = 1 : Since arr[j] > pivot, do nothing
// No change in i and arr[]
j = 2 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 1
arr[] = {10, 30, 80, 90, 40, 50, 70} // We swap 80 and 30
j = 3 : Since arr[j] > pivot, do nothing
// No change in i and arr[]
j = 4 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 2
arr[] = {10, 30, 40, 90, 80, 50, 70} // 80 and 40 Swapped
j = 5 : Since arr[j] <= pivot, do i++ and swap arr[i] with arr[j]
i = 3
arr[] = {10, 30, 40, 50, 80, 90, 70} // 90 and 50 Swapped
We come out of loop because j is now equal to high-1.
Finally we place pivot at correct position by swapping
arr[i+1] and arr[high] (or pivot)
arr[] = {10, 30, 40, 50, 70, 90, 80} // 80 and 70 Swapped
Now 70 is at its correct place. All elements smaller than
70 are before it and all elements greater than 70 are after
it.
Implementation:
Following are C++, Java and Python implementations of QuickSort.
/* C implementation QuickSort */
#include<stdio.h>
// A utility function to swap two elements
void swap(int* a, int* b)
{
int t = *a;
*a = *b;
*b = t;
}
/* This function takes last element as pivot, places
the pivot element at its correct position in sorted
array, and places all smaller (smaller than pivot)
to left of pivot and all greater elements to right
of pivot */
int partition (int arr[], int low, int high)
{
int pivot = arr[high]; // pivot
int i = (low - 1); // Index of smaller element
for (int j = low; j <= high- 1; j++)
{
// If current element is smaller than or
// equal to pivot
if (arr[j] <= pivot)
{
i++; // increment index of smaller element
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
/* The main function that implements QuickSort
arr[] --> Array to be sorted,
low --> Starting index,
high --> Ending index */
void quickSort(int arr[], int low, int high)
{
if (low < high)
{
/* pi is partitioning index, arr[p] is now
at right place */
int pi = partition(arr, low, high);
// Separately sort elements before
// partition and after partition
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
/* Function to print an array */
void printArray(int arr[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", arr[i]);
printf(" ");
}
// Driver program to test above functions
int main()
{
int arr[] = {10, 7, 8, 9, 1, 5};
int n = sizeof(arr)/sizeof(arr[0]);
quickSort(arr, 0, n-1);
printf("Sorted array: ");
printArray(arr, n);
return 0;
}
Output:
Sorted array:
1 5 7 8 9 10
Analysis of QuickSort
Time taken by QuickSort in general can be written as following.
T(n) = T(k) + T(n-k-1) + θ(n)
The first two terms are for two recursive calls, the last term is for the partition process. k is the number of elements which are smaller than pivot.
The time taken by QuickSort depends upon the input array and partition strategy. Following are three cases.
Worst Case: The worst case occurs when the partition process always picks greatest or smallest element as pivot. If we consider above partition strategy where last element is always picked as pivot, the worst case would occur when the array is already sorted in increasing or decreasing order. Following is recurrence for worst case.
T(n) = T(0) + T(n-1) + θ(n)
which is equivalent to
T(n) = T(n-1) + θ(n)
The solution of above recurrence is θ(n2).
Best Case: The best case occurs when the partition process always picks the middle element as pivot. Following is recurrence for best case.
T(n) = 2T(n/2) + θ(n)
The solution of above recurrence is θ(nLogn). It can be solved using case 2 of Master Theorem.
Average Case:
To do average case analysis, we need to Consider all possible permutation of array and calculate time taken by every permutaion which doesn`t look easy.
We can get an idea of average case by considering the case when partition puts O(n/9) elements in one set and O(9n/10) elements in other set. Following is recurrence for this case.
T(n) = T(n/9) + T(9n/10) + θ(n)
Solution of above recurrence is also O(nLogn)
Although the worst case time complexity of QuickSort is O(n2) which is more than many other sorting algorithms like Merge Sort and Heap Sort, QuickSort is faster in practice, because its inner loop can be efficiently implemented on most architectures, and in most real-world data. QuickSort can be implemented in different ways by changing the choice of pivot, so that the worst case rarely occurs for a given type of data. However, merge sort is generally considered better when data is huge and stored in external storage.
FAQs on Sorting Algorithms - GATE Computer Science Engineering(CSE) 2026 Mock Test Series - Computer Science Engineering (CSE)
| 1. What is the time complexity of Selection Sort? |  |
| 2. How does Merge Sort work? |  |
| 3. What is the main advantage of using QuickSort over other sorting algorithms? |  |
| 4. How does Heap Sort differ from Merge Sort? |  |
| 5. Can Bubble Sort be recommended for sorting large datasets? |  |