Abstractions from Precipitation | Engineering Hydrology - Civil Engineering (CE) PDF Download
Evaporation and its Measurement
Evaporation is a cooling process in which the latent heat of evaporation of about 585 cal/gm is provided by the water body. in this process liquid changes into gaseous phase at free surface, below the boiling point through the transfer of heat energy.
Dalton’s Law
The rate of evaporation is proportional to the difference between the saturation vapour pressure at the water temperature, es and the actual vapour pressure in the air ea thus
E = K(es - ea)
Where, E = Rate if evaporation (mm/day)
es = Saturation vapour pressure of air (mm)
ea = Actual vapour pressure of air (mm)
es - ea Saturation deficiency
Measurement of Evaporation
- ISI standard pan
Lake evaporation = Cp × pan evaporation
Where, Cp pan coefficient
= 0.8 for ISI pan
= 0.7 for class A-Pan - Empirical Evaporation Equations (Meyer’s Formula) E = km(es - ea)[1 + (V9 / 16]
Where, km = Coefficients which accounts for size of water body.
= 0.36 (for large deep water)
∼ 0.50 (for small and shallow waters)
es = Saturation vapour pressure of air in mm of Hg.
ea = Actual vapour pressure of overlying air in mm at Hg at specified height of 8 m.
V9 = monthly mean wind velocity in km/hr at about 9 m above the ground level.
1/7th power Law
V1 / V2 = (H1 / H2)1/7
Where, V1 is the wind velocity at height H1 and V2 is the wind velocity at height H2.
Water Budget Method
This is simplest method bit it is least reliable it is used for rough calculation, it is based on mass conversation principle.
P + Vis + Vig + Vog + E + ΔS + TL
Where, P=Daily precipitation on the water surface.
Vis = Daily surface inflow into take.
Vos = Daily surface outflow from lake.
Vig = Daily underground inflow into the lake.
Vog = Daily underground outflow from the lake.
E = Daily Evaporation
ΔS = change in storage of lake
= +ve if increase in storage
= -ve if decrease in storage
TL = Daily transpiration loss from the plants on the lake.
Energy Budget Method
The energy budget method is an application of the law of conservation of energy. The energy available for evaporation is determined by considering the incoming energy. Outgoing energy and energy stored in the water body over a known time interval.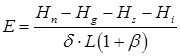
Where, Hn = Net heat energy received by the water surface
Hn = Hc(1 - r) - Hb
Hc(1 - r) = incoming solar radiation into a surface of reflection coefficient, r
Hb = Back radiation from water body
Hg = Heat flux into the ground
HS = Heat stored in water body
Hi = Net heat conducted out the system by water flow (advected energy)
β = Bowen’s ratio
δ = Density of water
L = Latent heat of evaporation.
Evapo-Transpiration
While transpiration takes place, the land are in which plants stand also lose moisture by the evaporation of water from soil and water bodies. In hydrology and irrigation practive, it is found that evaporation and transpiration processes can be considered advantageously under one head as evapo-transpiration.
The real evapo-transpiration occurring in a specific situation is called actual evapo-transpiration (AET).
Penman’s Method
Penman’s equation is based on sound theoretical reasoning and is obtained by a combination of the energy balance and mass transfer approach.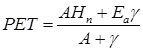
Where, PET = daily evaporation in mm/day.
A = slope of the saturation vapour pressure v/s temperature curve at the mean air temperature in mm of Hg per °C.
Hn = Net radiation in mm of evaporable water per day
Ea = Parameter including wind velocity and saturation deficit.
γ = Psychometric constant
= 0.49 mm of Hg/°C
It is based on mass transfer and energy balance.
Transpiration Loss (T)
T = (w1 + w2) - w2
Where, w1 = Initial weight of the instrument
W = Total weight of water added for full growth of plant.
w2 = Final weight of instruction including plant and water
T = Transpiration loss.
Stream Flow Measurement
Streamflow representing the runoff phase of the hydrologic cycle is the most important basic data for hydrologic studies.
Streamflow measurement techniques can be broadly classified into two categories as:
- Direct determination and
- Indirect determination.
Under each category there are a host of methods. The important ones are listed below:
- Direct determination of stream discharge
(a) Area velocity methods
(b) Dilution techniques
(c) Electromagnetic method and
(d) ultrasonic method - Indirect determination of streamflow
(a) Hydraulic structures, such as weirs, flumes and gated structures, and
(b) Slope- area method
Determination of Velocity
- Float Method: Float are generally used to determine approximate velocity of the surface, these are floating devices which are passed with the water along the flow of stream.
Vs = L / t Here, Vs = surface velocity
L= Distance travelled by the float in time ‘t’. - Current Meters Method: These consists of rotating elements which rotate due to reactions of stream currents. The number of revolution per second are counted. This can be used to measure point velocity of ant depth.
V = aNs + b
Where, V = point velocity
Ns = Number of revolution per sec. a and b are current meters constant.
Velocity Distribution
-
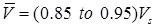
For turbulent flow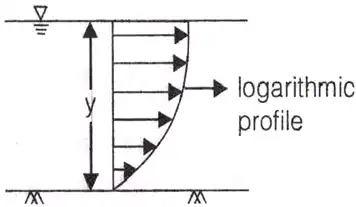 Where, mean velocity
Where, mean velocity
Vs = surface velocity - For shallow streams
 where
where  point velocity at 0.6 y from surface
point velocity at 0.6 y from surface - For Deep streams
Sounding Weight W = weight in newton
W = weight in newton 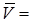 Average stream velocity
Average stream velocity
Y = Depth of flow in meters.
Stream Flow (discharge measurement)
- Area Velocity Method: This method of discharge measurement consists essentially of measuring the area of cross-section of the river at a selected section called the gauging site and measuring the velocity of flow through the cross-sectional area. The gauging site must be selected with care to assure that the stage-discharge curve is reasonably constant over a long period of about a few years.
Total discharge,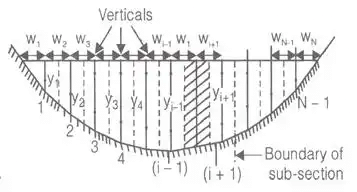
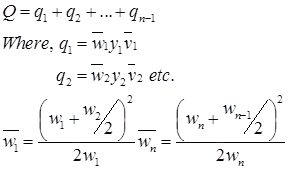
- Moving Boat Method: in this method a special propeller type current meter which is free to move about a vertical axis is towed in a boat at a velocity VB at right angles to stream flow. If the flow velocity is VF the meter will align itself in the direction of the resultant velocity VR making an angle θ with the direction of the boat. Further. The meter will ragister the velocity VR if VB IS normal VF.
 VB = VRcosθ
VB = VRcosθ
VF=VRsinθ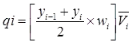
Where, qi = Discharge through the ith segment.
qi = ((Yi-1 + yi) / 2)V2R sinθ.cosθ.ti
ti = Time required to pass the boat through ith segment. - Dilution Method: the dilution method of flow measurement, also known as the chemical method depends upon the continuity principle applied to a tracer which is allowed to mix completely with the flow.
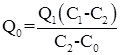
This technique in which Q0 is estimated by knowing C1, C2, C0 and Q1 is known as constant rate injection method or plateau gauging.
Where,
Q0 = Discharge of stream
C0 = Tracer intensity initially
C1 = Tracer intensity at (1)
C2 = Tracer intensity at (2).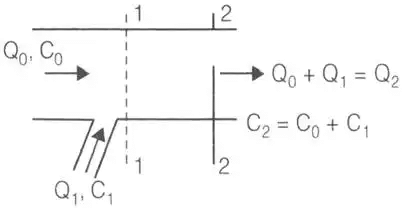 Q1 and Q2 are discharge at (1) and (2) respectively.
Q1 and Q2 are discharge at (1) and (2) respectively. - Slope Area Method: it is a very versatile indirect method of discharge estimation and requires
(i) the selection of a reach in which cross-sectional properties including bed elevations are known at its ends.
(ii) the value of Manning’s n and
(iii) water-surface elevations at the two end sections.
(a)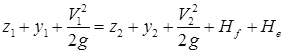 Where Hf = Frictional losses
Where Hf = Frictional losses
He = Eddy losses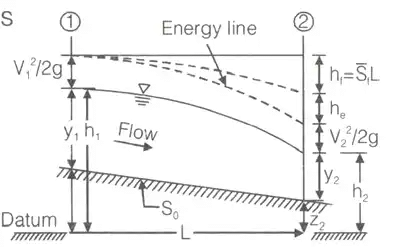 (b)
(b)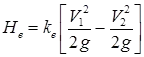
ke = Eddy loss coefficients.
(c)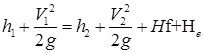
(d)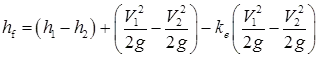
(e)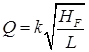 Where, Q = stream flow (m3/sec)
Where, Q = stream flow (m3/sec)
(f) k = (k1 . k2... kn)1/n Where, k = Conveyance
(g) k = 1/n . A . R2/3 Where, A = area (m2)
R = Hydraulic mean depth
= Area / wetted perimeter
|
20 videos|43 docs|30 tests
|
FAQs on Abstractions from Precipitation - Engineering Hydrology - Civil Engineering (CE)
| 1. What is precipitation in civil engineering? |  |
| 2. How does precipitation impact civil engineering projects? |  |
| 3. What are the methods used in civil engineering to measure precipitation? |  |
| 4. How does climate change affect precipitation in civil engineering? |  |
| 5. What are the design considerations for civil engineering projects related to precipitation? |  |





















