Year 3 Exam > Year 3 Notes > Year 3 Mathematics > Add by making 10
Add by making 10 | Year 3 Mathematics PDF Download
Bridging Through 10
Here's how it works:
- Work out what you need to add to your first number to make ten.
- Take this amount from your second number. What remains?
- Add the remainder to 10. That's your answer!
Solved Examples
Example 1: Method 1
8 + 4 = ?
This can be solved by partitioning one of the numbers.
Here are two tens frames showing 8 orange counters.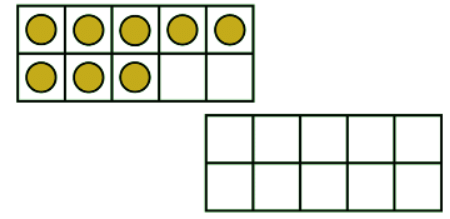
Here are 4 yellow counters which are going to be added to the 8 orange counters.
There are 2 empty spaces on the left hand ten frame.
8 + 2 = 10
We have used 2 of the yellow counters to make 10.
There are 2 yellow counters left over that are added to the second ten frame.
10 + 2 = 12
This shows 8 + 4 = 12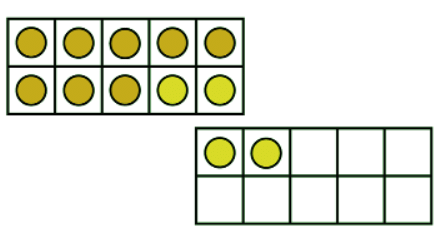
Method 2: The same calculation can be solved using the part-whole model.
4 can be split into 2 and 2.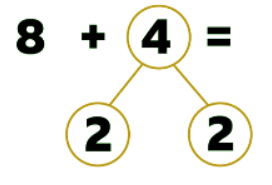
2 can be added to 8 to make 10.
8 + 2 = 10
Then the 10 can be added to the other 2 to make 12.
10 + 2 = 12
Which means 8 + 4 = 12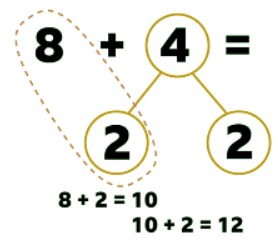
Example 2: 7 + 4 = ?
Start by working out what you need to add to 7 to make 10.
7 + ? = 10
The answer is 3.
Take this answer away from the second number in the calculation.
4 - 3 = 1
Add this answer on to 10.
10 + 1 = 11
So:
7 + 4 = 11.
This can be shown as a part-whole model like this.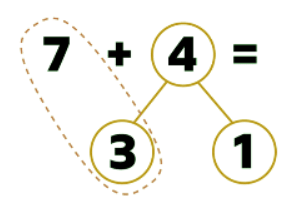
The document Add by making 10 | Year 3 Mathematics is a part of the Year 3 Course Year 3 Mathematics.
All you need of Year 3 at this link: Year 3
|
69 videos|67 docs|11 tests
|
FAQs on Add by making 10 - Year 3 Mathematics
| 1. How can students improve their math skills by bridging through 10? |  |
Ans. Students can improve their math skills by practicing addition and subtraction problems that involve bridging through 10. This can help them develop a better understanding of number relationships and mental math strategies.
| 2. Why is bridging through 10 an important concept in elementary math education? | |
Ans. Bridging through 10 is an important concept in elementary math education because it helps students develop number sense and mental math skills. It also lays the foundation for more advanced math concepts in the future.
| 3. What are some strategies that students can use to bridge through 10 effectively? | |
Ans. Some strategies that students can use to bridge through 10 effectively include breaking numbers into parts, using number lines, and practicing mental math exercises. These strategies can help students become more confident in their math abilities.
| 4. How can teachers incorporate bridging through 10 into their math lessons? | |
Ans. Teachers can incorporate bridging through 10 into their math lessons by providing students with practice problems that require them to bridge across 10. They can also use manipulatives and visual aids to help students visualize the concept.
| 5. What are some real-life applications of bridging through 10 in everyday situations? | |
Ans. Some real-life applications of bridging through 10 in everyday situations include calculating change at a store, estimating quantities when shopping, and determining the time difference between two events.
Related Exams
About this Document
|
Dec 22, 2024 Last updated |
Document Description: Add by making 10 for Year 3 2024 is part of Year 3 Mathematics preparation.
The notes and questions for Add by making 10 have been prepared according to the Year 3 exam syllabus. Information about Add by making 10 covers topics
like Bridging Through 10, Solved Examples and Add by making 10 Example, for Year 3 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Add by making 10.
Introduction of Add by making 10 in English is available as part of our Year 3 Mathematics
for Year 3 & Add by making 10 in Hindi for Year 3 Mathematics course.
Download more important topics related with notes, lectures and mock test series for Year 3
Exam by signing up for free. Year 3: Add by making 10 | Year 3 Mathematics
Description
Full syllabus notes, lecture & questions for Add by making 10 | Year 3 Mathematics - Year 3 | Plus excerises question with solution to help you revise complete syllabus for Year 3 Mathematics | Best notes, free PDF download
Information about Add by making 10
In this doc you can find the meaning of Add by making 10 defined & explained in the simplest way possible. Besides explaining types of
Add by making 10 theory, EduRev gives you an ample number of questions to practice Add by making 10 tests, examples and also practice Year 3
tests
|
Explore Courses for Year 3 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
shortcuts and tricks
,Add by making 10 | Year 3 Mathematics
,ppt
,Extra Questions
,practice quizzes
,MCQs
,Semester Notes
,Add by making 10 | Year 3 Mathematics
,Summary
,Objective type Questions
,Important questions
,past year papers
,Free
,Viva Questions
,Add by making 10 | Year 3 Mathematics
,Exam
,video lectures
,Previous Year Questions with Solutions
,study material
,Sample Paper
,mock tests for examination
;
Additional Information about Add by making 10 for Year 3 Preparation
Add by making 10 Free PDF Download
The Add by making 10 is an invaluable resource that delves deep into the core of the Year 3 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Add by making 10 now and kickstart your journey towards success in the Year 3 exam.
Importance of Add by making 10
The importance of Add by making 10 cannot be overstated, especially for Year 3 aspirants.
This document holds the key to success in the Year 3 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Add by making 10 Notes
Add by making 10 Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Add by making 10.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Add by making 10 Notes on EduRev are your ultimate resource for success.
Add by making 10 Year 3 Questions
The "Add by making 10 Year 3 Questions" guide is a valuable resource for all aspiring students preparing for the
Year 3 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Add by making 10 on the App
Students of Year 3 can study Add by making 10 alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Add by making 10,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Add by making 10 is prepared as per the latest Year 3 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup