Additional Questions: Applications of Derivatives | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Match the Following
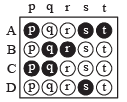
This question contains statements given in two columns, which have to be matched. The statements in Column-I are labelled A, B, C and D, while the statements in Column-II are labelled p, q, r, s and t. Any given statement in Column-I can have correct matching with ONE OR MORE statement(s) in ColumnII. The appropriate bubbles corresponding to the answers to these questions have to be darkened as illustrated in the following example :
If the correct matches are A-p, s and t; B-q and r; C-p and q; and D-s then the correct darkening of bubbles will look like the given.
Q. 1. In this questions there are entries in columns I and II. Each entry in column I is related to exactly one entry in column II. Write the correct letter from column II against the entry number in column I in your answer book.
Let the functions defined in column I have domain 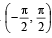
Column I Column II
(A) x + sin x (p) increasing
(B) sec x (q) decreasing
(r) neither increasing nor decreasing
Ans. (A) → p (B) → r
Solution. (A) f (x) = x + sin x on (–π/2, π/2)
f ' (x) = 1 + cos x
As 0 < cos x < 1 for x ∈ (–π/2, π/2)
∴ f ' (x) > 0 on (–π/2, π/2)
(A) → p
(B) f (x) = sec x ⇒ f ' (x) = sec x tan x.
Clearly f ' (x) < 0 in (–π/2, 0) and f ' (x) > 0 in (0, π/2)
∴ 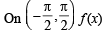 is neither increasing non decreasing.
is neither increasing non decreasing.
(B) → r
Integer Value Correct Type
Q. 1. The maximum value of the function
f (x) = 2x3 – 15x2 + 36x – 48 on the set
A= {x | x2 + 20 < 9x} is
Ans. 7
Solution. The given function is f (x) = 2x3 - 15 x2 + 36x- 48
and A = {x | x2 + 20 < 9x}
⇒ A = {x | x2 - 9x + 20 < 0}
⇒ A = {x | (x - 4)(x - 5) < 0} ⇒ A = [4, 5]
Also f '( x) = 6x2 - 30x+ 36 = 6(x2 - 5x+ 6)
= 6( x - 2)(x- 3)
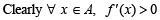
∴ f is strictly increasing function on A.
∴ Maximum value of f on A
= f (5) = 2 x 53 - 15 x 52 + 36 x 5- 48
= 250 – 375 + 180 – 48 = 430 – 423 = 7
Q. 2. Let p(x) be a polynomial of degree 4 having extremum at 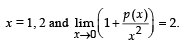
Then the value of p (2) is
Ans. 0
Solution. 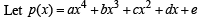
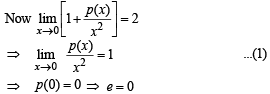
Applying L’Hospital’s rule to eqn (1), we get
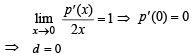
Again applying L ‘Hospital’s rule, we get
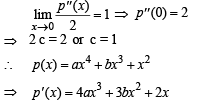
As p(x) has extremum at x = 1 and 2
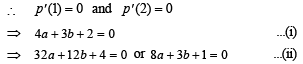
Solving eq’s (i) and (ii) we get 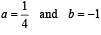
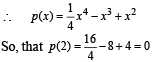
Q. 3. Let f be a real-valued differentiable function on R (the set of all real numbers) such that f(1) = 1. If the y-intercept of the tangent at any point P(x, y) on the curve y = f(x) is equal to the cube of the abscissa of P, then find the value of f(–3)
Ans. 9
Solution. The equation of tangent to the curve y = f (x) at the point P (x,y) is
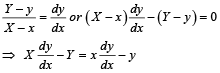
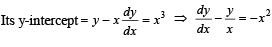
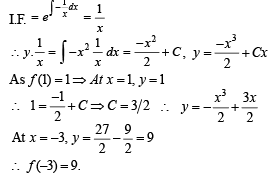
Q. 4. Let f be a function defined on R (the set of all real numbers) such that f '(x)=2010 (x–2009) (x–2010)2 (x–2011)3 (x–2012)4 .for all x ∈ R. If g is a function defined on R with values in the interval (0, ∞) such that f (x)=ln ( g (x)), for all x ∈ R then the number of points in R at which g has a local maximum is
Ans. 1
Solution. We have ,
f '(x) = 2010 (x – 2009)(x – 2010)2 ( x – 2011)3 (x – 2012)4
As f (x) = ln g (x) ⇒ g ( x) = e f (x) ⇒ g '(x) = e f (x) . f '(x)
For max/min, g '( x) = 0 ⇒ f '(x)= 0
Out of two points one should be a point of maxima and other that of minima.
∴ There is only one point of local maxima.
Q. 5. let f : IR → IR be defined as f (x) = |x| +|x2- 1|. The total number of points at which f attains either a local maximum or a local minimum is
Ans. 5
Solution. We have f (x) = |x| +|x2- 1|
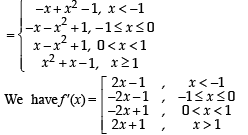
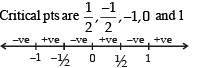
We observe at five points f ’(x) changes its sign
∴ There are 5 points of local maximum or local minimum.
Q. 6. Let p(x) be a real polynomial of least degree which has a local maximum at x = 1 and a local minimum at x = 3. If p(1) = 6 and p(3) = 2, then p’(0) is
Ans. 9
Solution. ∴ p(x) has a local maximum at x = 1 and a local minimum at x = 3 and p(x) is a real polynomial of least degree
∴ Let p'(x) = k (x – 1)(x – 3 ) = k(x2 – 4x + 3)
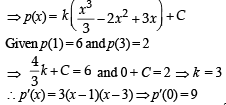
Q. 7. A vertical line passing through the point (h, 0) intersects the ellipse 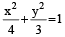 at the points P and Q. Let the tangents to the ellipse at P and Q meet at the point R. If Δ(h) = area of the triangle
at the points P and Q. Let the tangents to the ellipse at P and Q meet at the point R. If Δ(h) = area of the triangle 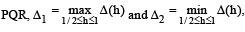
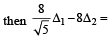
Ans. 9
Solution. Vertical line x = h, meets the ellipse 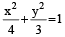 at
at
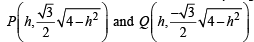
By symmetry, tangents at P and Q will meet each other at x-axis.
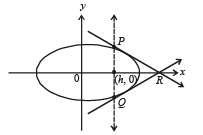
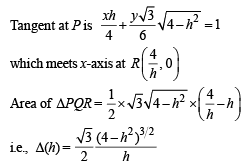
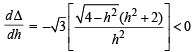
∴ Δ(h) is a decreasing function.
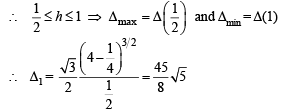
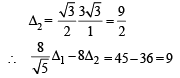
Q. 8. The slope of the tangent to the curve (y – x5)2 = x(1 + x2)2 at the point (1, 3) is
Ans. 8
Solution.
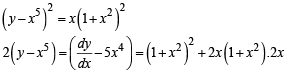
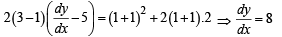
Q. 9. A cylindrical container is to be made from certain solid material with the following constraints: It has a fixed inner volume of V mm3, has a 2 mm thick solid wall and is open at the top. The bottom of the container is a solid circular disc of thickness 2 mm and is of radius equal to the outer radius of the container.
If the volume of the material used to make the container is minimum when the inner radius of the container is 10 mm, then the value of 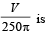
Ans. 4
Solution. Let r be the internal radius and R be the external radius.
Let h be the internal height of the cylinder.
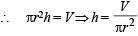
Also Vol. of material 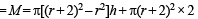
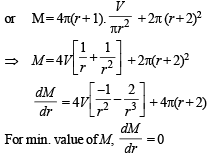
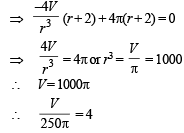
|
347 docs|185 tests
|
















