Additional Questions: Matrices and Determinants | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Match the Following
Each question contains statements given in two columns, which have to be matched. The statements in Column-I are labelled A, B, C and D, while the statements in Column-II are labelled p, q, r, s and t. Any given statement in Column-I can have correct matching with ONE OR MORE statement(s) in ColumnII. The appropriate bubbles corresponding to the answers to these questions have to be darkened as illustrated in the following example :
If the correct matches are A-p, s and t; B-q and r; C-p and q; and D-s then the correct darkening of bubbles will look like the given.

Q.1. Consider the lines given by
L1 : x + 3y – 5 = 0; L2 : 3x – ky – 1 = 0; L3 : 5x + 2y – 12 = 0
Match the Statements / Expressions in Column I with the Statements / Expressions in Column II and indicate your answer by darkening the appropriate bubbles in the 4 × 4 matrix given in the ORS.
Column I Column II
(A) L1, L2, L3 are concurrent, if (p) k = –9
(B) One of L1, L2, L3 is parallel to at least one of the other two, if 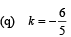
(C) L1, L2, L3 from a triangle, if (r) k = 5/6
(D)L1, L2, L3 do not form a triangle, if (s) k = 5
Ans. (A) → s; (B) → p, q; (C) → r; (D) → p, q, s
Solution. The given lines are
L1: x+3y -5 = 0
L2 : 3x - ky - 1 = 0
L3 :5x + 2y -12 = 0
(A) Three lines L1, L2,L3 are concurrent if
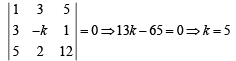
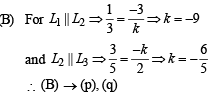
(C) Three lines L1, L2, L3 will form a triangle if no two of them are parallel and no three are concurrent
∴ k ≠ 5, –9, – 6/5
∴ (C) → r
(D) L1, L2,L3 do not form a triangle if either any two of these are parallel or the three are concurrent i.e. k = 5, – 9 , – 6/5
∴ (D) → (p), (q ), (s)
Q.2. Match the Statements/Expressions in Column I with the Statements / Expressions in Column II and indicate your answer by darkening the appropriate bubbles in the 4 × 4 matrix given in the ORS.
Column I Column II
(A) The minimum value of 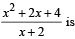 (p) 0
(p) 0
(B) Let A and B be 3 × 3 matrices of real numbers, where A is (q) 1
symmetric, B is skew-symmetric, and (A + B) (A – B) = (A – B)
(A + B). If (AB)t = (–1)k AB, where (AB)t is the transpose of the
matrix AB, then the possible values of k are
(C) Let a = log3 log3 2. An integer k satisfying 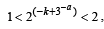 (r) 2
(r) 2
must be less than
(D) If sin θ = cosφ , then the possible values of 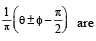 (s) 3
(s) 3
Ans. (A) → r; (B) → q, s; (C) → r, s; (D) → p, r
Solution.
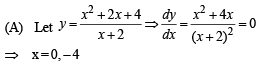
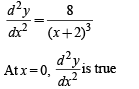
∴ y is min when x = 0, ∴ y min = 2
(B) As A is symmetric and B is skew symmetric matrix, we should have
At = A and Bt = – B ...(1)
Also given that (A + B) (A – B) = (A– B) (A + B)
⇒ A2 - AB + BA -B2 = A2 + AB - BA-B2
⇒ 2BA = 2AB or AB = BA ...(2)
Now given that
(AB)t = (-1)kAB
⇒ (BA)t = (-1)kAB (using equation (2))
⇒ At Bt = (-1)kAB
⇒ –AB = (–1)k AB [using equation(1)]
⇒ k should be an odd number
∴ (B) → (q), (s) (C)
Given that a = log3 log3 2
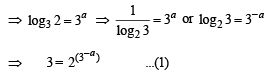
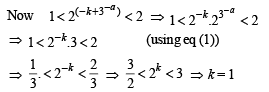
∴k is less than 2 and 3
∴ (C) → (r), (s).
(D) 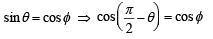
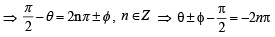
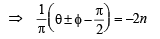
∴ Here possible values of 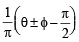 are 0 and 2 for
are 0 and 2 for
n = 0, –1.
∴ D → (p) ,(r).
|
347 docs|185 tests
|
FAQs on Additional Questions: Matrices and Determinants - JEE Advanced - 35 Years Chapter wise Previous Year Solved Papers for JEE
| 1. What is a matrix and how is it used in linear algebra? |  |
| 2. What is the determinant of a matrix and how is it calculated? |  |
| 3. How are matrices multiplied together? |  |
| 4. What are the properties of determinants? |  |
| 5. How are determinants used in solving systems of linear equations? |  |
















