Algebra of Fourth Order Tensors - Civil Engineering (CE) PDF Download

Algebra of fourth order tensors

A fourth order tensor A may be thought of as a linear function that maps second order tensor A into another second order tensor B. While this is too narrow a viewpoint1 , it suffices for the study of mechanics. We write B = A : A which defines a linear transformation that assigns a second order tensor B to each second order tensor A.
We can express any fourth order tensor, A in terms of the three Cartesian basis vectors as

A = A_ijkle_i ⊗ ej ⊗ ek ⊗ el ,                              (2.117)

where A_ijkl are the Cartesian components of A. Thus, the fourth order tensor A has 3⁴ = 81 components. Remember that any repeated index has to be summed from one through three.
One example for a fourth order tensor is the tensor product of the four vectors u, v, w, x, denoted by u ⊗ v ⊗ w ⊗ x. We have the useful property:

(u ⊗ v) ⊗ (w ⊗ x) = u ⊗ v ⊗ w ⊗ x.                            (2.118)

If A = u ⊗ v ⊗ w ⊗ x, then it is easy to see that the Cartesian components of A, A_ijkl = u_iv_jw_kx_l , where u_i , v_j , w_k, x_l are the Cartesian components of the vectors u, v, w and x respectively.

Another example of a fourth order tensor, is the tensor obtained from the tensor product of two second order tensors, i.e., D = A ⊗B, where A, B are second order tensors and D is the fourth order tensor. In index notation we may write: D_ijkl = A_ijB_kl where D_ijkl, A_ij , Bkl are the Cartesian components of the respective tensors.

The double contraction of a fourth order tensor A with a second order tensor B results in a second order tensor, denoted by A : B with the property that:

(u ⊗ v ⊗ w ⊗ x) : (y ⊗ z)           =               (w · y)(x · z)(u ⊗ v),                               (2.119)
(y ⊗ z) : (u ⊗ v ⊗ w ⊗ x)           =               (u · y)(v · z)(w ⊗ x).                               (2.120)

Hence, we can show that the components of A, A_ijkl can be expressed as

A_ijkl = (e_i ⊗ e_j ) · A : (e_k ⊗ e_l) = (ei ⊗ e_j ) : A · (e_k ⊗ e_l)                  (2.121)

Next, we compute the Cartesian components of



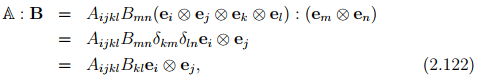
where A_ijkl and B_mn are the Cartesian components of the tensors A and B. Note that B : A ≠ A : B.
Then, the following can be established:

(A ⊗ B) : C = (B · C)A,                                      (2.123)
A : (B ⊗ C) = (A · B)C,                                      (2.124)

where A, B, C and D are second order tensors.
The unique transpose of a fourth order tensor A denoted by A^t is governed by the identity

B · A^t : C = C · A : B = A : B · C                          (2.125)

for all the second order tensors B and C. From the above identity we deduce the index relation (A^t )_ijkl = A_klij . The following properties of fourth order tensors can be established:

(A^t )^t = A,                                        (2.126)
(A ⊗ B)^t = B ⊗ A.                          (2.127)

Next, we define fourth order unit tensors I and  II  so that

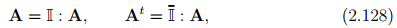
for any second order tensor A. These fourth order unit tensors may be represented by


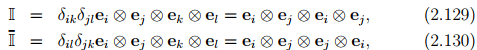
where (I)_ijkl = δ_ikδ_jl and 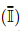 _ijkl = δ_ilδ_jk define the Cartesian components of I and  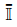, respectively. Note tha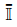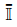t ≠ ^t .
The deviatoric part of a second order tensor A may be described by means of a fourth order projection tensor, P where



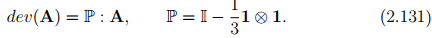
Thus the components of dev(A) and A are related through the expression [dev(A)]_ij = P_ijklA_kl, with P_ijkl = δ_ikδ_jl − (1/3)δ_ijδ_kl.
Similarly, the fourth order tensors S and W given by



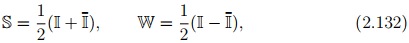
are such that for any second order tensor A, they assign symmetric and skew part of A respectively, i.e.,




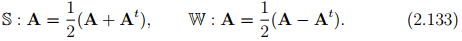
Alternate representation for tensors 
Till now, we represented second order tensor components in a matrix form, for the advantages that it offers in computing other quantities and defining other operators. However, when we want to study mapping of second order tensor on to another second order tensor, this representation seem to be inconvenient. For this purpose, we introduce this alternate representation. Now, we view the second order tensor as a column vector of nine components instead of a 3 by 3 matrix as introduced in (2.45). The order of these components is subjective. Keeping in mind the application of this is to study elasticity, we order the components of a general second order tensor, A, as,
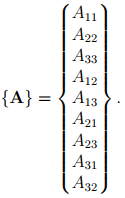                                                                              (2.134)
In view of this, the fourth order tensor, which for us is a linear function that maps a second order tensor to another second order tensor, can be represented as a 9 by 9 matrix as,



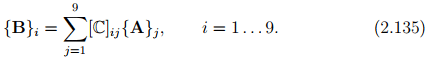
where A and B are second order tensors and C is a fourth order tensor. Note that as before the fourth order tensor has 81 (=9*9) components. Thus, now the fourth order tensor is a matrix which is the reason for representing the second order tensor as vector.