Algebra of second order tensors
A second order tensor A, for our purposes here, may be thought of as a linear function that maps a directed line segment to another directed line segment. This we write as, v = Au where A is the linear function that assigns a vector v to each vector u. Since A is a linear function,
A(αu + βv) = αAu + βAv, (2.37)
for all vectors u, v and all scalars α, β.
If A and B are two second order tensors, we can define the sum A + B, the difference A − B and the scalar multiplication αA by the rules
(A � B)u = Au � Bu, (2.38)
(αA)u = α(Au), (2.39)
where u denotes an arbitrary vector. The important second order unit (or identity) tensor 1 and the second order zero tensor 0 are defined, respectively, by the relation 1u = u and 0u = o, for all (∀) vectors u.
If the relation v � Av ≥ 0 holds for all vectors, then A is said to be a positive semi-definite tensor. If the condition v�Av > 0 holds for all nonzero vectors v, then A is said to be positive definite tensor. Tensor A is called negative semi-definite if v � Av ≤ 0 and negative definite if v � Av < 0 for all vectors, v ≠ o, respectively.
The tensor (or direct or matrix) product or the dyad of the vectors u and v is denoted by u ⊗ v. It is a second order tensor which linearly transforms a vector w into a vector with the direction of u following the rule
(u ⊗ v)w = (v � w)u. (2.40)
The dyad satisfies the linearity property
(u ⊗ v)(αw + βx) = α(u ⊗ v)w + β(u ⊗ v)x. (2.41)
The following relations are easy to establish:
(αu + βv) ⊗ w = α(u ⊗ w) + β(v ⊗ (2.42)
(u ⊗ v)(w ⊗ x) = (v � w)(u ⊗ x), (2.43)
A(u ⊗ v) = (Au) ⊗ v, (2.44)
where, A is an arbitrary second order tensor, u, v, w and x are arbitrary vectors and α and β are arbitrary scalars. Dyad is not commutative, i.e.,
u ⊗ v ≠ v ⊗ u and (u ⊗ v)(w ⊗ x) ≠ (w ⊗ x)(u ⊗ v).
A dyadic is a linear combination of dyads with scalar coefficients, for example, α(u ⊗ v) + β(w ⊗ x). Any second-order tensor can be expressed as a dyadic. As an example, the second order tensor A may be represented by a linear combination of dyads formed by the Cartesian basis {ei}, i.e.,
A = Aijei ⊗ ej The nine Cartesian components of A with respect to {ei}, represented by Aij can be expressed as a matrix [A], i.e.,
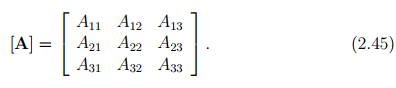
This is known as the matrix notation of tensor A. We call A, which is resolved along basis vectors that are orthonormal and fixed, a Cartesian tensor of order two. Then, the components of A with respect to a fixed, orthonormal basis vectors ei is obtained as:
The Cartesian components of the unit tensor 1 form the Kronecker delta symbol, thus 1 = δijei ⊗ ej = ei ⊗ ei and in matrix form that
Next we would like to derive the components of u ⊗ v along an orthonormal basis {ei}. Using the representation (2.46) we find that
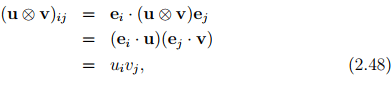
where ui and vj are the Cartesian components of the vectors u and v respectively. Writing the above equation in the convenient matrix notation we have
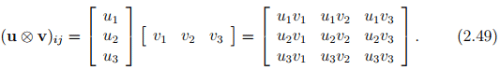
The product of two second order tensors A and B denoted by AB is again a second order tensor. It follows from the requirement (AB)u = (Bu) , for all vectors u.
Further, the product of second order tensors is not commutative, i.e., AB ≠ BA. The components of the product AB along an orthonormal basis {ei} is found to be:
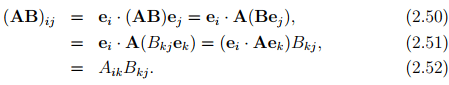
The following properties hold for second order tensors:
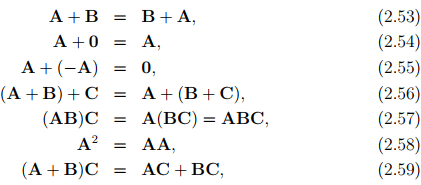
Note that the relations AB = 0 and Au = o does not imply that A or B is 0 or u = o.
The unique transpose of a second order tensor A denoted by At is governed by the identity:
v � Atu = u � Av (2.60)
for all vectors u and v. Some useful properties of the transpose are
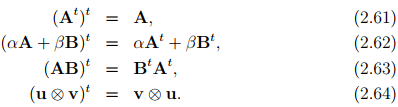
From identity (2.60) we obtain ei � Atej = ej � Aei , which gives, in regard to equation (2.46), the relation (At )ij = Aji. The trace of a tensor A is a scalar denoted by tr(A) and is defined as:
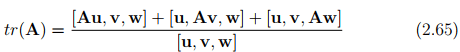
where u, v, w are any vectors such that [u, v, w] ≠ 0, i.e., these vectors span the entire 3D vector space. Thus, tr(m ⊗ n) = m � n. Let us see how: Without loss of generality we can assume the vectors u, v and w to be m, n and (m ∧ n) respectively. Then, (2.65) becomes
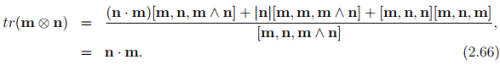
The following properties of trace is easy to establish from (2.65):
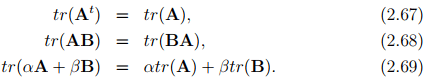
Then, the trace of a tensor A with respect to the orthonormal basis {ei} is given by
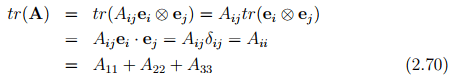
The dot product between two tensors denoted by A � B, just like the dot product of two vectors yields a real value and is defined as
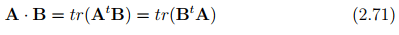
Next, we record some useful properties of the dot operator:
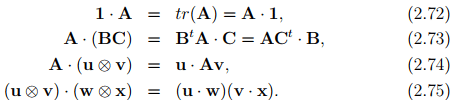
Note that if we have the relation A�B = C�B, in general, we cannot conclude that A equals C. A = C only if the above equality holds for any arbitrary B.
The norm of a tensor A is denoted by |A| (or ||A||). It is a non-negative real number and is defined by the square root of A � A, i.e.,
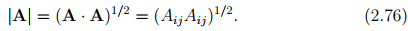
The determinant of a tensor A is defined as:
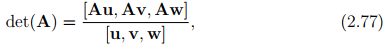
where u, v, w are any vectors such that [u, v, w] ≠ 0, i.e., these vectors span the entire 3D vector space. In index notation:
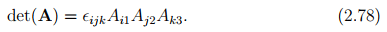
Then, it could be shown that
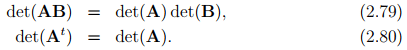
A tensor A is said to be singular if and only if det(A) = 0. If A is a non-singular tensor i.e., det(A) ≠ 0, then there exist a unique tensor A−1 , called the inverse of A satisfying the relation
If tensors A and B are invertible (i.e., they are non-singular), then the properties
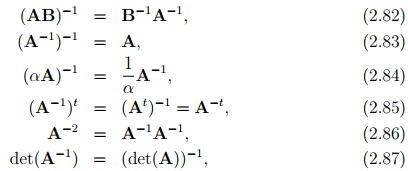
hold.
Corresponding to an arbitrary tensor A there is a unique tensor A* , called the adjugate of A, such that
for any arbitrary vectors a and b in the vector space. Suppose that A is invertible and that a, b, c are arbitrary vectors, then
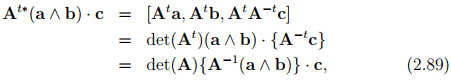
where successive use has been made of equations (2.88), (2.81), (2.63), (2.77) and (2.60). Because of the arbitrariness of a, b, c there follows the connection
between the inverse of A and the adjugate of At .
Orthogonal tensor
An orthogonal tensor Q is a linear function satisfying the condition
for all vectors u and v. As can be seen, the dot product is invariant (its value does not change) due to the transformation of the vectors by the orthogonal tensor. The dot product being invariant means that both the angle, θ between the vectors u and v and the magnitude of the vectors |u|, |v| are preserved. Consequently, the following properties of orthogonal tensor can be inferred:
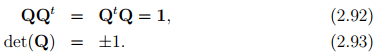
It follows from (2.92) that Q−1 = Qt . If det(Q) = 1, Q is said to be proper orthogonal tensor and this transformation corresponds to a rotation. On the other hand, if det(Q) = −1, Q is said to be improper orthogonal tensor and this transformation corresponds to a reflection superposed on a rotation.
Figure 2.2 shows what happens to two directed line segments, u1 and v1 under the action the two kinds of orthogonal tensors. A proper orthogonal tensor corresponding to a rotation about the e3 basis, whose Cartesian coordinate components are given by
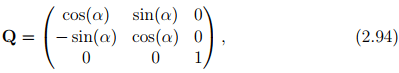
transforms,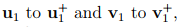 
maintaining their lengths and the angle between these line segments. Here 
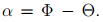An improper orthogonal
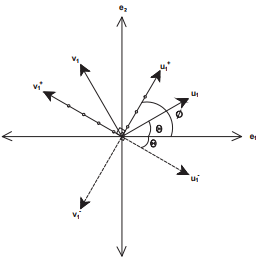
Figure 2.2: Schematic of transformation of directed line segments u1 and v1 under the action of proper orthogonal tensor to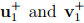 
as well as by improper orthogonal tensor to 
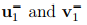respectively.
tensor corresponding to reflection about e1 axis, whose Cartesian coordinate components are given by
(2.95)
transforms, u1 to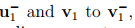 
still maintaining their lengths and the angle between these line segments a constant.
Symmetric and skew tensors
A symmetric tensor, S and a skew symmetric tensor, W are such:
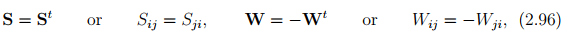
therefore the matrix components of these tensor reads
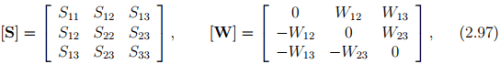
thus, there are only six independent components in symmetric tensors and three independent components in skew tensors. Since, there are only three independent scalar quantities that in a skew tensor, it behaves like a vector with three components. Indeed, the relation holds:
Wu = ω ∧ u, (2.98)
where u is any vector and ω characterizes the axial (or dual) vector of the skew tensor W, with the property |ω| = |W|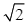 
(proof is omitted). The relation between the Cartesian components of W and ω is obtained as:
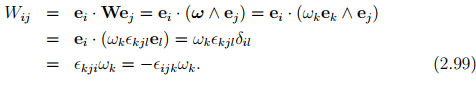
Thus, we get
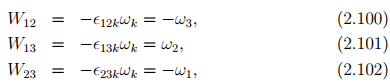
where the components W12, W13, W23 form the entries of the matrix [W] as characterized in (2.97)b.
Any tensor A can always be uniquely decomposed into a symmetric tensor, denoted by S (or sym(A)), and a skew (or antisymmetric) tensor, denoted by W (or skew(A)). Hence, A = S + W, where
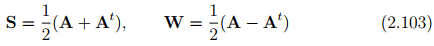
Next, we shall look at some properties of symmetric and skew tensors:
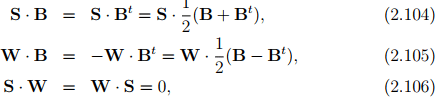
where B denotes any second order tensor. The first of these equalities in the above equations is due to the property of the dot and trace operator, namely A � B = At � Bt and that A � B = B � A.
Projection tensor
Consider any vector u and a unit vector e. Then, we write u = u|| + u⊥, with uk and u⊥ characterizing the projection of u onto the line spanned by e and onto the plane normal to e respectively. Using the definition of a tensor product (2.40) we deduce that
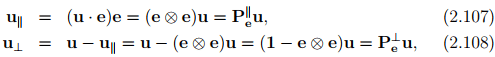
where
are projection tensors of order two. A tensor P is a projection if P is symmetric and Pn = P where n is a positive integer, with properties:
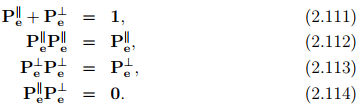
Spherical and deviatoric tensors
Any tensor of the form α1, with α denoting a scalar is known as a spherical tensor.
Every tensor A can be decomposed into its so called spherical part and its deviatoric part, i.e.,
where α = tr(A)/3 = Aii/3 and dev(A) is known as a deviator of A or a deviatoric tensor and is defined as dev (A) = A − (1/3)tr(A)1, or [dev(A)]ij = Aij − (1/3)Akkδij . It then can be easily verified that tr(dev(A)) = 0, for any second order tensor A.
Polar Decomposition theorem
Above we saw two additive decompositions of an arbitrary tensor A. Of comparable significance in continuum mechanics are the multiplicative decompositions afforded by the polar decomposition theorem. This result states that an arbitrary invertible tensor A can be uniquely expressed in the forms
A = QU = VQ, (2.116)
where Q is an orthogonal tensor and U, V are positive definite symmetric tensors. It should be noted that Q is proper or improper orthogonal according as det(A) is positive or negative.
