Algebra of Vectors - Civil Engineering (CE) PDF Download

Algebra of vectors
A physical quantity, completely described by a single real number, such as temperature, density or mass is called a scalar. A vector is a directed line element in space used to model physical quantities such as force, velocity, acceleration which have both direction and magnitude. The vector could be denoted as v or 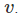 Here we denote vectors as v. The length of the directed line segment is called as the magnitude of the vector and is denoted by |v|. Two vectors are said to be equal if they have the same direction and magnitude. The point that vector is a geometric object, namely a directed line segment cannot be overemphasized. Thus, for us a set of numbers is not a vector.
 

The sum of two vectors yields a new vector, based on the parallelogram law of addition and has the following properties:

u + v = v + u,                                         (2.1)
(u + v) + w = u + (v + w),                      (2.2)
u + o = u,                                              (2.3)
u + (−u) = o,                                         (2.4)

where o denotes the zero vector with unspecified direction and zero length, u, v, w are any vectors. The parallelogram law of addition has been proposed for the vectors because that is how forces, velocities add up.
Then the scalar multiplication αu produces a new vector with the same direction as u if α > 0 or with the opposite direction to u if α < 0 with the following properties:

(αβ)u = α(βu),                                     (2.5)
(α + β)u = αu + βu,                            (2.6)
α(u + v) = αu + αv,                             (2.7)

where α, β are some scalars(real number).

The dot (or scalar or inner) product of two vectors u and v denoted by u � v assigns a real number to a given pair of vectors such that the following properties hold:

u � v = v � u,                                                 (2.8)
u � o = 0,                                                     (2.9)
u � (αv + βw) = α(u � v) + β(u � w),             (2.10)
u � u > 0,   for all u ≠  o,     and
u � u = 0, if and only if     u = o.                   (2.11)

The quantity |u| (or ||u||) is called the magnitude (or length or norm) of a vector u which is a non-negative real number is defined as

|u| = (u � u)^1/2 ≥ 0.                                      (2.12)

A vector e is called a unit vector if |e| = 1. A nonzero vector u is said to be orthogonal (or perpendicular) to a nonzero vector v if: u � v = 0. Then, the projection of a vector u along the direction of a vector e whose length is unity is given by: u � e

So far algebra has been presented in symbolic (or direct or absolute) notation. It represents a very convenient and concise tool to manipulate most of the relations used in continuum mechanics. However, particularly in computational mechanics, it is essential to refer vector (and tensor) quantities to a basis. Also, for carrying out mathematical operations more intuitively it is often helpful to refer to components.

We introduce a fixed set of three basis vectors e₁, e₂, e₃ (sometimes introduced as i, j, k) called a Cartesian basis, with properties:

e₁ � e₂ = e₂ � e₃ = e₃ � e₁ = 0, e₁ � e₁ = e₂ � e₂ = e₃ � e₃ = 1,                            (2.13)

so that any vector in three dimensional space can be written in terms of these three basis vectors with ease. However, in general, it is not required for the basis vectors to be fixed or to satisfy (2.13). Basis vectors that satisfy (2.13) are called as orthonormal basis vectors.
Any vector u in the three dimensional space is represented uniquely by a linear combination of the basis vectors e₁, e₂, e₃, i.e.
 

u = u₁e₁ + u₂e₂ + u₃e_3,                                         (2.14)

where the three real numbers u₁, u_2, u₃ are the uniquely determined Cartesian components of vector u along the given directions e₁, e₂, e₃, respectively. In other words, what we are doing here is representing any directed line segment as a linear combination of three directed line segments. This is akin to representing any real number using the ten arabic numerals.
If an orthonormal basis is used to represent the vector, then the components of the vector along the basis directions is nothing but the projection of the vector on to the basis directions. Thus,

u₁ = u � e₁, u₂ = u � e₂, u₃ = u � e_3.                            (2.15)

Using index (or subscript or suffix) notation relation (2.14) can be written as 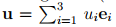 or, in an abbreviated form by leaving out the summation symbol, simply

as u = u_ie_i , (sum over i = 1,2,3),                                (2.16)

where we have adopted the summation convention, invented by Einstein. The summation convention says that whenever an index is repeated (only once) in the same term, then, a summation over the range of this index is implied unless otherwise indicated. The index i that is summed over is said to be a dummy (or summation) index, since a replacement by any other symbol does not affect the value of the sum. An index that is not summed over in a given term is called a free (or live) index. Note that in the same equation an index is either dummy or free. Here we consider only the three dimensional space and denote the basis vectors by {e_i}_i∈{1,2,3} collectively.
In light of the above, relations (2.13) can be written in a more convenient form as
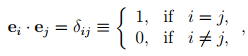                                                   (2.17)

where δ_ij is called the Kronecker delta. It is easy to deduce the following identities:

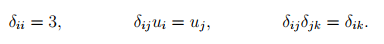            (2.18)

The projection of a vector u onto the Cartesian basis vectors, e_i yields the i^th component of u. Thus, in index notation u � e_i = u_i .
As already mentioned a set of numbers is not a vector. However, for ease of computations we represent the components of a vector, u obtained with respect to some basis as,

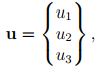                               (2.19)

instead of writing as u = u_ie_i using the summation notation introduced above. The numbers u₁, u₂ and u₃ have no meaning without the basis vectors which are present even though they are not mentioned explicitly.
If u_i and v_j represents the Cartesian components of vectors u and v respectively, then,

                                      

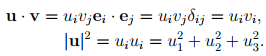
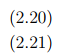
Here we have used the replacement property of the Kronecker delta to write v_jδ_ij as v_i which reflects the fact that only if j = i is δ_ij = 1 and otherwise δ_ij = 0. The cross (or vector) product of u and v, denoted by u ∧ v produces

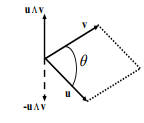
Figure 2.1: Cross product of two vectors u and v

a new vector satisfying the following properties:

u ∧ v = −(v ∧ u),                                                                                       (2.22)
(αu) ∧ v = u ∧ (αv) = α(u ∧ v),                                                                  (2.23)
u ∧ (v + w) = (u ∧ v) + (u ∧ w),                                                                  (2.24)
u ∧ v = o, iff u and v are linearly dependent                                             (2.25)

when u ≠ o v ≠ o. Two vectors u and v are said to be linearly dependent if u = αv, for some constant α. Note that because of the first property the cross product is not commutative.
The cross product characterizes the area of a parallelogram spanned by the vectors u and v given that

u ∧ v = |u||v|sin(θ)n,                                                                                 (2.26)

where θ is the angle between the vectors u and v and n is a unit vector normal to the plane spanned by u and v, as shown in figure 2.1. In order to express the cross product in terms of components we introduce the permutation (or alternating or Levi-Civita) symbol ∈_ijk which is defined as


with the property ∈_ijk = ∈_ijk = ∈_ijk , ∈_ijk = −∈_ijk and ∈_ijk = −∈_ijk, respectively. Thus, for an orthonormal Cartesian basis, {e_1, e₂, e₃}, e_i ∧ e_j = ∈_ijke_k It could be verified that ∈ijk may be expressed as:


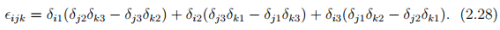
It could also be verified that the product of the permutation symbols ∈_ijk∈_pqr is related to the Kronecker delta by the relation



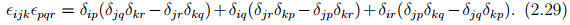
We deduce from the above equation (2.29) the important relations:



The triple scalar (or box) product: [u, v, w] represents the volume V of a parallelepiped spanned by u, v, w forming a right handed triad. Thus, in index notation:

V = [u, v, w] = (u ∧ v) � w = ∈_ijku_iv_jw_k.                                                                       (2.31)

Note that the vectors u, v, w are linearly dependent if and only if their scalar triple product vanishes,
i.e., [u, v, w] = 0
The product (u ∧ v) ∧ w is called the vector triple product and it may be verified that



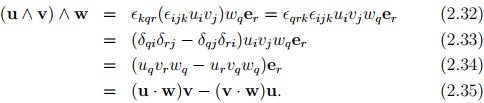
Similarly, it can be shown that

u ∧ (v ∧ w) = (u � w)v − (u � v)w.                                                                           (2.36)

Thus triple product, in general, is not associative, i.e., u∧ (v∧ w) ≠ (u∧ v)∧ w