Algebraic Identities - Polynomials, Class 9, Mathematics PDF Download
| Table of contents |

|
| Algebraic Identities |

|
| Identity For The Square Of Trinomial |

|
| Identity For The Cube Of A Binomial |

|
| Sum And Difference Of Cube |

|
| Conditional Identity |

|
| Type Of Factorization |

|
"Polynomials" is a chapter in Class 9 Mathematics that focuses on the study of algebraic expressions and polynomials, with a particular emphasis on "Algebraic Identities." Through this chapter, students gain an understanding of a range of algebraic identities and the properties of polynomials.
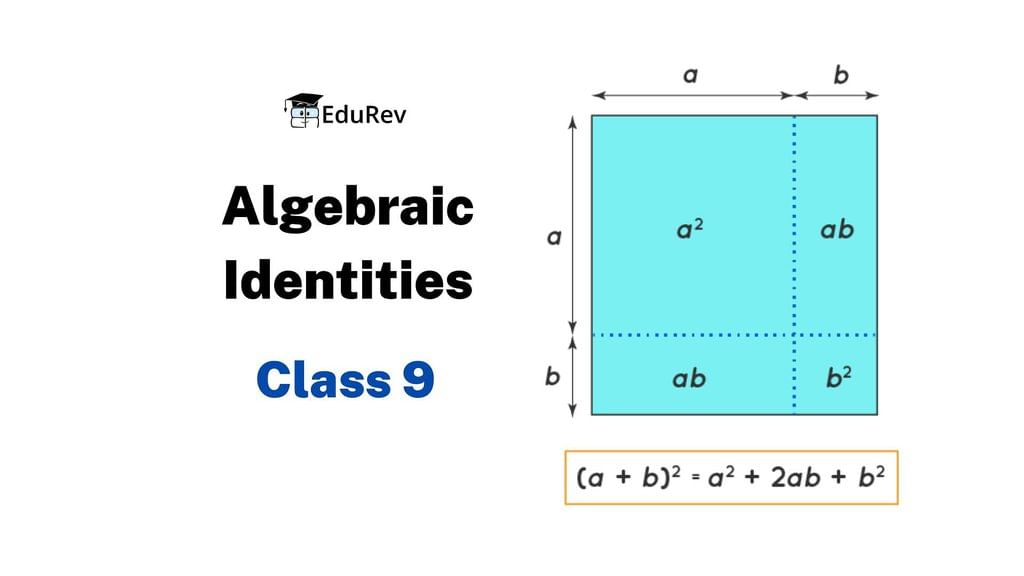
Algebraic Identities
Let us recall the following algebraic identities is earlier.
- (a + b)2 = a2 + 2ab + b2
- (a – b)2 = a2 – 2ab + b2
- (a + b) (a – b) = a2 – b2
- (x + a) (x + b) = x2 + (a + b) x + ab
Ex. Expand each of the following :
(i) (2x + 3y)2
(ii) (4x – 5y)2
(iii) (x + 5) (x + 6)
(iv) (x – 3) (x – 5)
Sol. (i) (2x + 3y)2 = (2x)2 + 2.2x.3y + (3y)2
[∵ (a + b)2 = a2 + 2ab + b2]
= 4x2 + 12xy + 9y2
(ii) (4x – 5y)2 = (4x)2 + 2.4x.5y + (5y)2
[∵ (a – b)2 = a2 – 2ab + b2]
= 16x2 – 40xy + 25y2
(iii) (x + 5) (x + 6) = x2 + (5 + 6)x + 5.6
[∵ (x + a) (x + b) = x2 + (a + b) x + ab]
= x2 + 11x + 30
(iv) (x – 3) (x – 5) = {x + (–3)} {x + (–5)}
[∵ (x + a) (x + b) = x2 + (a + b) x + ab]
= x2 + {(–3) + (–5)}x + (–3).(–5) = x2 + (–3 – 5)x + 15 = x2 – 8x + 15
Ex. Find the product using appropriate identities :
(i) (x + 8) (x + 8)
(ii) (3x – 2y) (3x – 2y)
(iii) (x + 0.1) (x – 0.1)
Sol. (i) (x + 8) (x + 8) = (x + 8)2 = x2 + 2(x) × 8 + (8)2 = x2 + 16x + 64.
(ii) (3x – 2y) (3x – 2y) = (3x – 2y)2
[∵ (a – b)2 = a2 – 2ab + b2]
= (3x)2 – 2(3x) × 2y + (2y)2 = 9x2 – 12xy + 4y2.
(iii) (x + 0.1) (x – 0.1) = (x)2 – (0.1)2
[∵ (a + b) (a – b) = a2 – b2]
= (x)2 – 0.01
Ex. Evaluate each of the following by using identities :
(i) 103 × 97
(ii) 103 × 103
(iii) (97)2
(iv) 185 × 185 – 115 × 115
Sol. (i) 103 × 97 = (100 + 3) (100 – 3) = (100)2 – (3)2 = 10000 – 9 = 9991
(ii) 103 × 103 = (103)2 = (100 + 3)2 = (100)2 + 2 × 100 × 3 + (3)2 = 10000 + 600 + 9 = 10609
(iii) (97)2 = (100 – 3)2 = (100)2 – 2 × 100 × 3 + (3)2 = 10000 – 600 + 9 = 9409
(iv)185 × 185 – 115 × 115 = (185)2 – (115)2 = (185 + 115) (185 – 115) = 300 × 70 = 21000
Identity For The Square Of Trinomial
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
Ex. Expand each of the following using suitable identities :
(i) (x + 2y + 4z)2
(ii) (– 2x + 5y – 3z)2
Sol. (i) (x + 2y + 4z)2 = (x)2 + (2y)2 + (4z)2 + 2.x.2y + 2.2y.4z + 2.4z.x
= x2 + 4y2 + 16z2 + 4xy + 16yz + 8zx
[∵ (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca]
(ii) (– 2x + 5y – 3z)2 = (–2x)2 + (5y)2 + (–3z)2 + 2.(–2x).5y + 2.5y.(–3z) + 2.(–3z).(–2x)
= 4x2 + 25y2 + 9z2 – 20xy – 30yz + 12zx
[∵ (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca]
Ex. If a2 + b2 + c2 = 20 and a + b + c = 0, find ab + bc + ca.
Sol. (a2 + b2 + c2) = a2 + b2 + c2 + 2ab + 2bc + 2ca
⇒ (a2 + b2 + c2) = a2 + b2 + c2 + 2(ab + bc + ca)
⇒ 02 = 20 + 2(ab + bc + ca)
⇒ –20 = 2(ab + bc + ca)
⇒ 
⇒ ab + bc + ca = – 10
Ex. If a + b + c = 9 and ab + bc + ca = 40, find a2 + b2 + c2.
Sol. We know that, (a2 + b2 + c2) = a2 + b2 + c2 + 2ab + 2bc + 2ca
⇒ 92 = a2 + b2 + c2 + 2 × 40
⇒ 81 = a2 + b2 + c2 + 80
⇒ a2 + b2 + c2 = 81 – 80
⇒ a2 + b2 + c2 = 1
Identity For The Cube Of A Binomial
(a + b)3 = a3 + b3 + 3ab (a + b)
(a – b)3 = a3 – b3 – 3ab (a – b)
Ex. Write the following in the expanded form :
(i) (3x + 4y)3 (ii) (2a – 3b)3
Sol. (i) (3x + 4y)3 = (3x)3 + (4y)3 + 3(3x) × 4y(3x + 4y)
(3x + 4y)3 = (3x)3 + (4y)3 + 3.(3x)2.4y + 3.(3x).(4y)2
[∵ (a + b)3 = a3 + b3 + 3ab (a + b)]
= 27x3 + 64y3 + 3.9x2.4y + 9x.16y2 = 27x3 + 64y3 + 108x2 y + 144xy2
(ii) (2a – 3b)3 = (2a)3 – (3b)3 – 3 × 2a × 3b(2a – 3b)
[∵ (a – b)3 = a3 – b3 – 3ab (a – b)]
= 8a3 – 27b3 – 18ab(2a – 3b)
= 8a3 – 27b3 – 18ab × 2a + 18ab × 3b
= 8a3 – 27b3 – 36a2b + 54ab2
Sum And Difference Of Cube
a3 + b3 = (a + b) (a2 – ab + b2)
a3 – b3 = (a – b) (a2 + ab + b2)
Ex. Factorize each of the following expressions :
1. x3 + 125
2. x3 – 0.027
Sol.
1. x3 + 125 = (x)3 + (5)3 = (x + 5) (x2 – x.5 + 52)
[∵ a3 + b3 = (a + b) (a2 – ab + b2)]
(x + 5) (x2 – 5x + 25)
2. x3 – 0.027 = (x)3 – (0.3)3 = (x – 0.3) [x2 + x × 0.3 + (0.3)2]
∵ [a3 – b3 = (a – b) (a2 + ab + b2)]
(x – 0.3x) (x2 + 0.3x + 0.09)
Conditional Identity
a3 + b3 + c3 – 3abc = (a + b + c) (a2 + b2 + c2 – ab – bc – ca)
If a + b + c = 0, then a3 + b3 + c3 = 3abc.
Ex. Find the product : (x + 2y + 3z) (x2 + 4y2 + 9z2 – 2xy – 6yz – 3zx)
Sol. (x + 2y + 3z) (x2 + 4y2 + 9z2 – 2xy – 6yz – 3zx)
= (x + 2y + 3z) (x2 + (2y)2 + (3z)2 – x × 2y – 2y × 3z – 3z × x)
= x3 + (2y)3 + (3z)2 – 3 × x × 2y × 3z
[∵ a3 + b3 + c3 – 3abc = (a + b + c) (a2 + b2 + c2 – ab – bc – ca)]
= x3 + 8y3 + 27z3 – 18xyz.
Ex. If a + b + c = 8 and ab + bc + ca = 20, find the value of a3 + b3 + c3 – 3abc.
Sol. Since (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
(a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca)
a + b + c = 8 and ab + bc + ca = 20,
(8)2 = a2 + b2 + c2 + 2 × 20
⇒ 64 = a2 + b2 + c2 + 40
∴ a2 + b2 + c2 = 64 – 40 = 24
We know that a3 + b3 + c3 – 3abc = (a + b + c) {a2 + b2 + c2 –(ab + bc + ca)}
∴ a3 + b3 + c3 – 3abc = 8 × (24 – 20) = 4 × 8 = 32
[∴ a + b + c = 8, ab + bc + ca = 20 and a2 + b2 + c2 = 24]
Thus, a3 + b3 + c3 – 3abc = 32.
Type Of Factorization
1.) Factorization by taking out the common factors
Ex. ab(a2 + b2 – c2) + bc (a2 + b2 – c2) – ca(a2 + b2 – c2)
Sol. We have ab(a2 + b2 – c2) + bc (a2 + b2 – c2) – ca(a2 + b2 – c2)
= (a2 + b2 – c2) (ab + bc – ca)
2.) Factorization by grouping the terms
Ex. (x2 + 3x)2 – 5(x2 + 3x) – y(x2 + 3x) +5y
Sol. We have
(x2 + 3x)2 – 5(x2 + 3x) – y(x2 + 3x) +5y
= (x2 + 3x) {(x2 + 3x) –5} – y{(x2 + 3x) –5} = (x2 + 3x – 5) (x2 + 3x – y)
3.) Factorization by making a perfect square
Ex. a2 + b2 – 2(ab – ac + bc)
Sol. We have
a2 + b2 – 2(ab – ac + bc)
= a2 + b2 – 2ab + 2ac – 2bc
= (a – b)2 + 2c (a – b)
= (a – b){(a – b) + 2c} = (a – b) (a – b + 2c)
4.) Factorization the difference of two squares
Ex. x8 – y8
Sol. We have
x8 – y8 = {(x4)2 – (y4)2} = (x4 – y4) (x4 + y4)
= {(x2)2 – (y2)2} (x4 + y4) = (x2 – y2) (x2 + y2) (x4 + y4)
= (x – y)(x + y)(x2 + y2) (x4 + y4)
= (x – y)(x + y)(x2 + y2){(x2)2 + (y2)2 + 2x2y2 – 2x2y2)
= (x – y)(x + y)(x2 + y2){(x2+ y2)2 – (√2xy)2}
= (x – y)(x + y)(x2 + y2)(x2+ y2 – √2xy)(x2 + y2 + √2xy)
Also Check at EduRev:
FAQs on Algebraic Identities - Polynomials, Class 9, Mathematics
| 1. What are algebraic identities? |  |
| 2. What is the identity for the square of a trinomial? |  |
| 3. What is the sum and difference of cubes identity? |  |
| 4. What is the identity for the cube of a binomial? |  |
| 5. What is a conditional identity? |  |

|
Explore Courses for Class 9 exam
|

|


















