Ampere's Circuital Law & Its Applications | Physics for JEE Main & Advanced PDF Download
In classical electromagnetism, Ampère's circuital law relates the circulation of a magnetic field around a closed loop to the electric current passing through the loop. This law is useful in finding the magnetic field due to currents under certain conditions of symmetry.
Ampere's Circuital Law
According to Ampere’s circuital equation, the line integral of a steady magnetic field across a closed loop is equal to μ0 times the total current (Ie) traveling through the surface bounded by the loop.
 Ampere's Law derivation from Biot- Savart's Law
Ampere's Law derivation from Biot- Savart's Law
Applications of Ampere's Circuital Law
Magnetic Field Due to a Straight Infinite Current-Carrying Wire
- Consider a current-carrying wire that is infinitely straight. We make an Amperian loop, which is a circle with a radius of r and a wire at its axis. As the magnetic field is tangential at all points on the loop, at all places, the magnetic field is of similar magnitude.
- Suppose the magnetic induction at point P, distance R from the wire is required.
- Draw the circle through P with center O and radius R as shown in the figure.
- The magnetic induction
at all points along this circle will be the same and will be tangential to the circle, which is also the direction of the length element

- Thus,
=
B × 2 πR. The current crossing of the circular area is i.
- Thus, by Ampere's law, B × 2πR = μ0i
⇒ B =
Note:
Line integral is independent of the shape of the path and the position of the wire within it.
The statement does not necessarily mean that
= 0 everywhere along the path but only that no net current is passing through the path.
Sign of current: The current due to which is produced in the same sense as (i.e. ) positive will be taken positive and the current which produces in the sense opposite to
will be negative.
Example 1: Find the value of the loops L1, L2, and L3 in the figure shown. The sense of is mentioned in the figure.
Solution: for L1
here I1 is taken positive because magnetic lines of force produced by I1 are clockwise as seen from the top. I2 produces lines of in a clockwise sense as seen from the top. The sense of is anticlockwise as seen from the top.
for L2 :
for L3 : 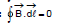

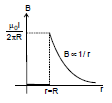
Special Case: To find out the magnetic field due to infinite current carrying wire
By B.S.L. 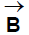 will have circular lines.
will have circular lines.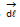 is also taken tangent to the circle
is also taken tangent to the circle
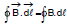 Therefore, θ = 0° so
Therefore, θ = 0° so = B 2πR (Therefore, B = const.)
Now by Ampere's law :
B 2πR = μ0I
Therefore, B =
Hollow current carrying infinitely long cylinder : (I is uniformly distributed on the) whole circumference
(i) 
By symmetry, the amperian loop is a circle.
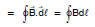
θ = 0
=
B = const.
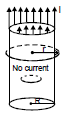
⇒ B =
(ii) r < R
=
= μ0 (0)
= B(2πr) = 0
⇒ Bin = 0
Solid infinite current-carrying cylinder
Assume current is uniformly distributed on the whole cross-section area
Take an American loop inside the cylinder. By symmetry it should be a circle whose center is on the axis of the cylinder and its axis also coincides with the cylinder axis on the loop.
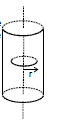
=
=
= B . 2πr =
B = =
⇒
=
Case (II) :
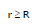
=
= B.(2pr) = m0. I
⇒ B = also
=
Example 2: Consider a coaxial cable that consists of an inner wire of radius a surrounded by an outer shell of inner and outer radii b and c respectively. The inner wire carries an electric current i0 and the outer shell carries an equal current in the opposite direction. Find the magnetic field at a distance x from the axis where (a) x < a, (b) a < x < b (c) b < x < c and (d) x > c. Assume that the current density is uniform in the inner wire and also uniform in the outer shell.
Sol.
A cross-section of the cable is shown in the figure. Draw a circle of radius x with the center at the axis of the cable. The parts a, b, c, and d of the figure correspond to the four parts of the problem. By symmetry, the magnetic field at each point of a circle will have the same magnitude and will be tangential to it. The circulation of B along this circle is, therefore,
in each of the four parts of the figure.
(a) The current enclosed within the circle in part b is i0 so that
Ampere's law
gives
B. 2πx = or, B =
The direction will be along the tangent to the circle.
(b) The current enclosed within the circle in part b is i0 so that
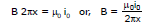
(c) The area of the cross-section of the outer shell is πc2 - πb2. The area of the cross-section of the outer shell within the circle in part c of the figure is πx2 - πb2.
Thus, the current through this part is . This is in the opposite direction to the current i0 in the inner wire. Thus, the net current enclosed by the circle is
inet = i0 - =
From Ampere's law,
B 2px = or, B =
(d) The net current enclosed by the circle in part d of the figure is zero and hence
B 2px = 0 or, B = 0.
Example 3(a): The figure shows a cross-section of a large metal sheet carrying an electric current along its surface. The current in a strip of width dl is Kdl where K is a constant. Find the magnetic field at a point P at a distance x from the metal sheet.
Sol. Consider two strips A and C of the sheet situated symmetrically on the two sides of P (figure). The magnetic field at P due to strip A is B0 perpendicular to AP and that due to the strip C is Bc perpendicular to CP. The resultant of these two is parallel to the width AC of the sheet. The field due to the whole sheet will also be in this direction. Suppose this field has magnitude B.
The field on the opposite side of the sheet at the same distance will also be B but in the opposite direction. Applying Ampere's law to the rectangle shown in the figure.
2B = μ0 K
or, B =
Note that it is independent of x.
|
320 videos|952 docs|172 tests
|
FAQs on Ampere's Circuital Law & Its Applications - Physics for JEE Main & Advanced
| 1. What is Ampere's Law and how does it relate to electromagnetism? |  |
| 2. Can Ampere's Law be used to calculate the magnetic field of any current-carrying wire? |  |
| 3. What are some practical applications of Ampere's Law? |  |
| 4. How does Ampere's Law differ from Faraday's Law of electromagnetic induction? |  |
| 5. Can Ampere's Law be used to calculate the magnetic field inside a current-carrying wire? |  |

















