Analytic functions - Complex variables | Engineering Mathematics - Engineering Mathematics PDF Download
| Table of contents |

|
| What is Analytic function? |

|
| Cauchy-Riemann Equations |

|
| Cauchy Integral Theorem |

|
| Taylor Series |

|
| Laurent series |

|
What is Analytic function?
A complex function is said to be analytic on a region R if it is complex differentiable at every point in R. The terms holomorphic function, differentiable function, and complex differentiable function are sometimes used interchangeably with "analytic function".
Cauchy-Riemann Equations
The Cauchy Riemann equations for a pair of given real-valued functions in two variables say, u (x, y) and v (x, y) are the following two equations:
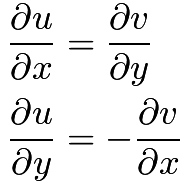
In a typical way, the values ‘u’ and ‘v’ are taken as the real and the imaginary parts of a complex-valued function of a single complex variable respectively,
z = x + iy
g(x + iy) = u(x, y) + iv(x, y)
if we are given that the functions u and v are differentiable at real values at a point in an open subset of the set of complex numbers that is C which can be taken as functions that are from R to R. This will imply that the partial derivatives of u and v do exist and thus we can also approximate smaller variations of ‘g’ in linear form. Then we say that g=u+iv is differentiable at complex values at that particular point iff the Cauchy Riemann equations at that point are satisfied by the partial derivatives of u and v.
Cauchy Riemann Equations in Polar Coordinates
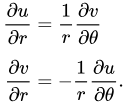
Cauchy Integral Theorem
If f(z) is analytic in some simply connected region R, then
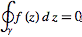
for any closed contour gamma completely contained in R. Writing z as
z = x + iy
f(z) = u + iv
then gives
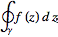 =
= 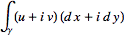
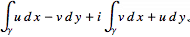
From Green's theorem,
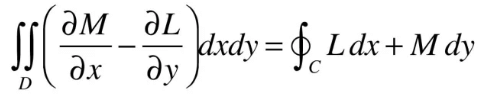
So,
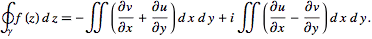
But the Cauchy-Riemann equations require that
∂u / ∂x = ∂v / ∂y
∂u / ∂y = - ∂v / ∂x,
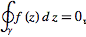
Taylor Series
Taylor Series for Holomorphic Functions. In Real Analysis, the Taylor series of a given function. f : R → R is given by: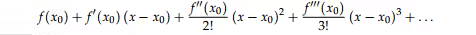
There are some convergence issues and applications of Taylor series. Also if the function f is infinitely differentiable everywhere on R, its Taylor series may not converge to that function. In contrast, there is no such issue in Complex Analysis: as long as the function f : C → C is holomorphic on an open ball B(z0), we can show the Taylor series of f.
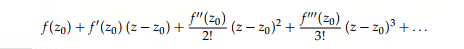
Laurent series
The Laurent series is a representation of a complex function f(z) as a series. Unlike the Taylor series which expresses f(z) as a series of terms with non-negative powers of z, a Laurent series includes terms with negative powers. A consequence of this is that a Laurent series may be used in cases where a Taylor expansion is not possible.
To calculate the Laurent series we use the standard and modified geometric series which are:
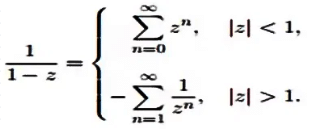 Here
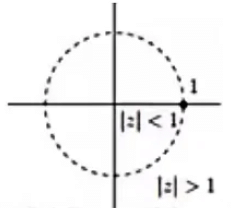
Here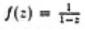 is analytic everywhere apart from the singularity at z = 1. Above are the expansions for f in the regions inside and outside the circle of radius 1. centred on z = 0. where ΙzΙ > 1 is the region outside the circle.
is analytic everywhere apart from the singularity at z = 1. Above are the expansions for f in the regions inside and outside the circle of radius 1. centred on z = 0. where ΙzΙ > 1 is the region outside the circle.
|
65 videos|129 docs|94 tests
|
FAQs on Analytic functions - Complex variables - Engineering Mathematics - Engineering Mathematics
| 1. What is the definition of an analytic function? |  |
| 2. What is the Cauchy Integral Theorem? |  |
| 3. How is a Taylor series used in complex analysis? |  |
| 4. What is the Laurent series expansion? |  |
| 5. How are analytic functions relevant in the field of complex variables? |  |




















