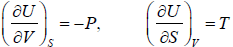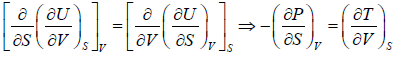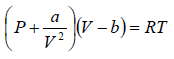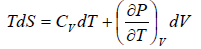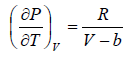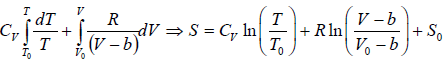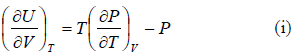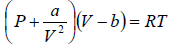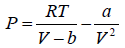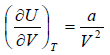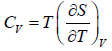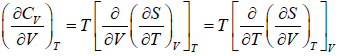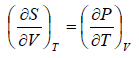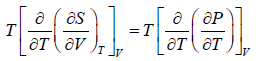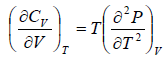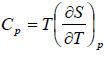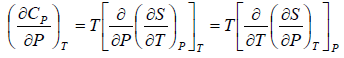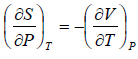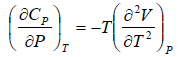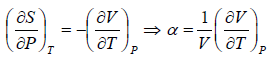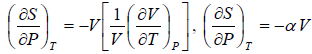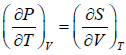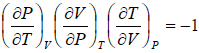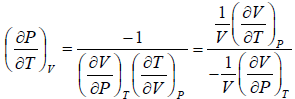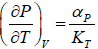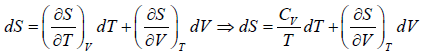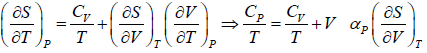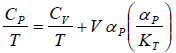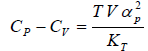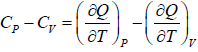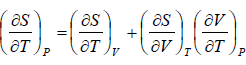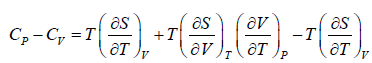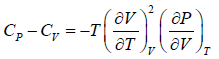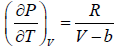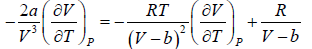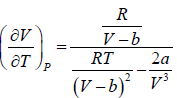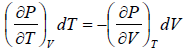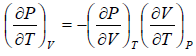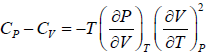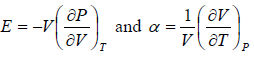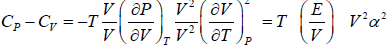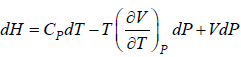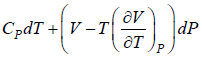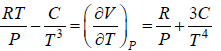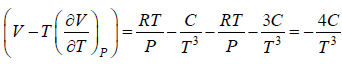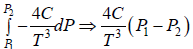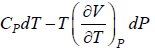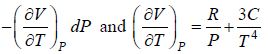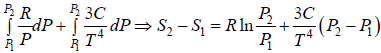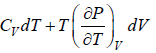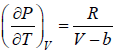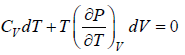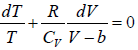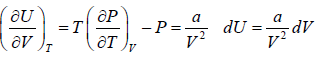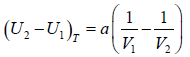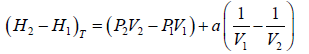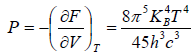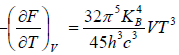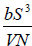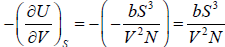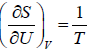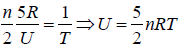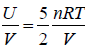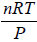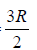Application of Maxwell Relation | Kinetic Theory & Thermodynamics - Physics PDF Download
First T - dS equation
Let T and V are independent variable, such that S = S(T,V)
dS = 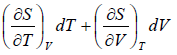
TdS = 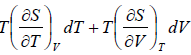 put
put 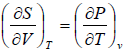
TdS = 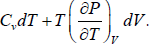
Second T - dS equation
Let T and P are independent variable, such that S = S(T, P).
TdS = 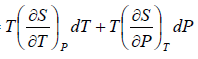
From Maxwell relation
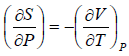
TdS = 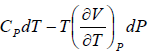
Third T - dS
Equation
Let P, V are independent variable, such that S = S(P, V).
dS = 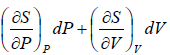
TdS = 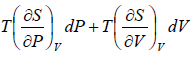 =
= 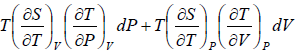
= 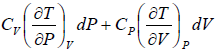
The First Energy Equation
Let T and V are independent variable, and U = U (T,V)
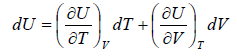
From first law of thermodynamics.
dU = TdS - PdV

Using Maxwell relation,
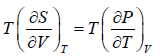
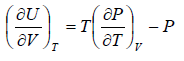
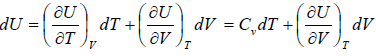
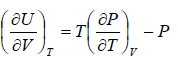
dU = 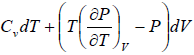
Second Energy Equation
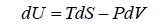
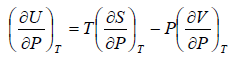
Using Maxwell relation
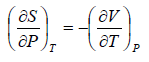
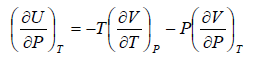
This is popularly known as second energy equation
Application of second energy equation:
If U is function of independent variable of T and P.
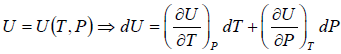
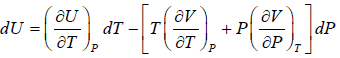
Example 2: From relation, dU = TdS - PdV, derive Maxwell relation, 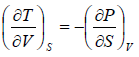
dU = TdS - PdV
Hence, U is exact differential
Example 3: A real gas which obey van der Waal’s equation of state are kept in container which has temperature T0 and volume V0 . If volume of container changes to V such that temperature of gas become T , then what is change in entropy?
Assume Cv is specific heat of constant volume
For van der Waal’s gas
From first T - dS equation
dS =
where, S0 is integration constant
Example 4: For van der Wall gases, prove that 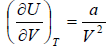 , where U is internal energy
, where U is internal energy
From first energy equation
put the value of
in equation (i)
Example 5: Prove that
(a) 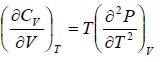
(b) 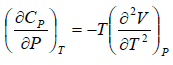
(a) We know that,
Using Maxwell relation,
One can get,
(b)
Use Maxwell relation,
Example 6: If αp is thermal expansivity at constant pressure and KT is isothermal compressibility, then prove that
(a) 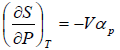
(b) 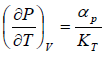
(c) 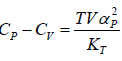
From Maxwell relation
(a)
(b)
(c)
Using Maxwell relation,

Example 7: Prove that
(a) 
(b) 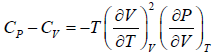
(c) For the van der Waal’s gas, prove that 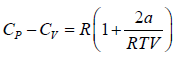
(a)
=
S = S(T,V)
and
Put the value of
in equation (A)
=
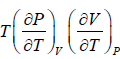
From Maxwell relation
From Maxwell relation
So
Put the value of
(b) For van der Waal’s gas
→ differentiate w.r.t. to T
Differentiate (B) with respect to V
Substituting the value
in equation
=
=
=
Example 8: From 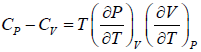
Prove, Cp - Cv = TEα2V, where E is bulk modulus of elasticity and α is coefficient of volume expansion.
Let Cp - Cv =
P = P(T,V)
For constant pressure dP = 0
Cp - Cv = TVEα2
Example 9: Prove that 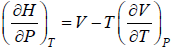
dH = TdS + VdP and put TdS =
dP in equation
Example 10: Over a certain range of pressure and temperature the Equation of a Certain substance is given by the relation V = 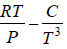
(a) Find the change in enthalpy at constant temperature if pressure change from P1 to P2
(b) Find the change of entropy of this substance in isothermal process
(a) dH =
for Isothermal process dT = 0
dH =
, V =
dH = H2 - H1 =
(b) From second TdS equation TdS =
For Isothermal process dT = 0
dS =
=
Example 11: For Vander Waal gas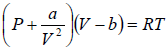
(a) Prove that 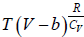 for Iso-Entropic process.
for Iso-Entropic process.
(b) If pressure and Volume changes from P1,V1 to P2,V2 at constant temperature then find Change in enthalpy
(a) From first TdS equation, TdS =
P =
⇒
At constant entropy dS = 0 ⇒
or
By integration,
= constant
(b) From
H =U + PV Hence enthalpy is point function
So, H1 =U1 + P1V1 and H2 = U2 + P2V2
H2 - H1 = U2 - U1 + P2V2 - P1V
Example 12: If Helmholtz free energy for radiation is given by F = 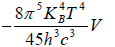
(a) What is radiation pressure?
(b) If S is entropy of the system, prove that specific heat at constant volume is given by Cv= 3S
(a) dF = -SdT - PdV
(b) S =
Cv =
=
=
Cv = 3S
Example 13: The internal energy E of a system is given by E = 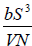 , where b is constant and other symbols have their usual meaning.
, where b is constant and other symbols have their usual meaning.
(a) Find the temperature of the system
(b) Find Pressure of the system
From first law of thermodynamics
TdS = dU + PdV ⇒dU = TdS - PdV
As, U = E =
(a) T =
(b) P =
Example 14: Consider an Ideal gas where entropy is given by S =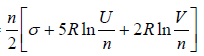 where n = number of moles, R = universal gas constant, U = internal energy V = volume and σ = constant
where n = number of moles, R = universal gas constant, U = internal energy V = volume and σ = constant
(a) Calculate specific heat at constant pressure and volume
(b) Prove that internal energy is given by U = 5/2PV
(a) From first law of thermodynamics
TdS = dU - PdV, dS =
⇒
∴
Cv =
⇒ Cp = Cv + R ⇒Cp = 7/2nR
(b) U =
⇒
PV = nRT ⇒ V =
⇒ U= 5/2PV
Example 15: Using the equation of state, PV = nRT and the specific heat per mole, 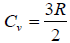 for monatomic ideal gas
for monatomic ideal gas
(a) Find Entropy of given system.
(b) Find free energy of given system
dU =
, P =
, Cv =
TdS = dU + PdV
dS =
or
S = 3/2
where, S0 is constant
(c) F = U - TS
=
where F0 = T.S0 is again constant
Example 16: From electromagnetic theory, Maxwell found that the pressure P from an isotropic radiation equal to 1/3 the energy density i.e., P = 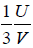 , where V is volume of the cavity, then using the first energy equation, prove that Energy density u is proportional to T4.
, where V is volume of the cavity, then using the first energy equation, prove that Energy density u is proportional to T4.
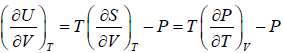
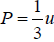 , where u =
, where u = 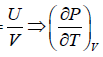 =
= 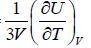
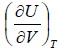 = u and u =
= u and u = 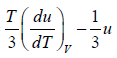
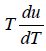 = 4u ⇒
= 4u ⇒ 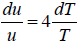
u ∝T4 ⇒ u = α T4 , where α is a constant.
|
6 videos|20 docs|32 tests
|
FAQs on Application of Maxwell Relation - Kinetic Theory & Thermodynamics - Physics
| 1. What is the first energy equation? |  |
| 2. What is the second energy equation? |  |
| 3. How can we apply Maxwell's relation in IIT JAM? |  |
| 4. What are some examples of applications of Maxwell's relation in IIT JAM? |  |
| 5. What are frequently asked questions about the first and second energy equations in IIT JAM? |  |