Approximate Stress Distribution method - Stress in Soil due to applied load, Soil Mechanics | Soil Mechanics Notes- Agricultural Engineering PDF Download
Approximate Stress Distribution method
In this method a 2:1 distribution of stress is assumed (as shown in Figure 6.2). If a rectangular area of B x L is loaded by uniformly distributed loadq, the vertical stress a depth of z below the loaded area can be determined as:
\[{\sigma _z}={{q(B \times L)} \over {(B + z) \times (L + z)}}\] (6.12)
The maximum stress is equal to average stress at depth equal to 2B. The maximum stress is greater than average stress if z < 2B and the maximum stress is less than average stress if z > 2B.
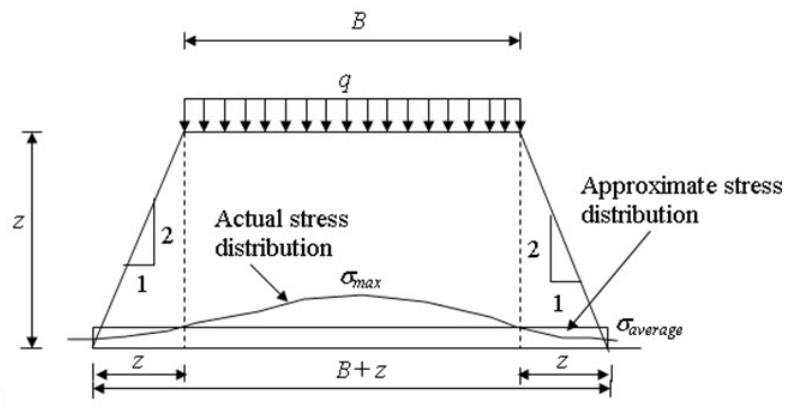
Fig. 6.2. Approximate stress calculation method.
Problem 1
Draw the vertical stress distribution due to a concentrated load (Q) of 50 kN acting on the surface of a soil for the following condition by using Boussinesq’s equation:
i) Variation of stress with depth for horizontal distance, r = 0 (points just vertically below the load) and r = 1m.
ii) Variation of stress with horizontal distance (either side of the load) for depth, z = 2m and z = 3m.
Solution
Equation (6.4) is used to calculate the vertical stress at any depth at any horizontal distance from the point of application of the concentration load. Figure 6.3 shows the variation of vertical stress with depth at horizontal distance, r = 0 and r = 1m. Keeping r value constant, the stress is calculated for different z values upto z = 8m. For example, at (r = 1m, z = 2m), the vertical stress is 4.22 kN/m2.
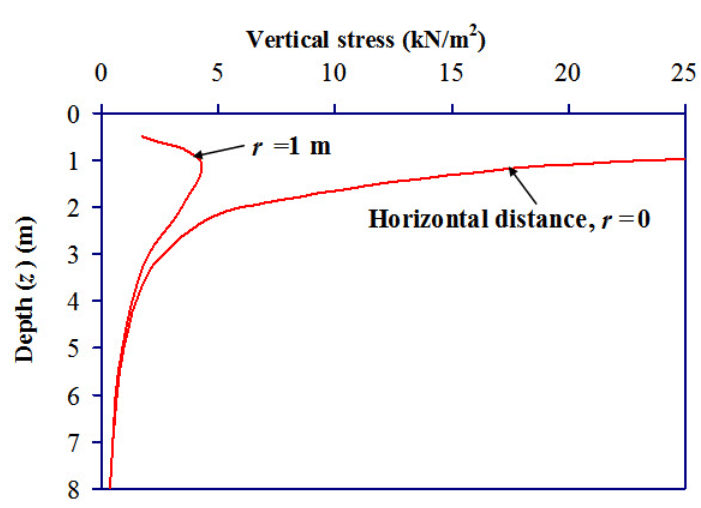
Fig. 6.3. Variation of vertical stress with depth.
Figure 6.4 shows variation of vertical stress with horizontal distance at depth z = 2m and z = 3m. It is observed that as the depth increases vertical stress decreases at the centre line. Same vertical stress is observed at different location with respect to depth and horizontal distance. For example, same vertical stress (2 kN/m2) is observed at (r = ± 1.5m, z = 2m) as well as at (r = ± 1 m, z = 3m). The line joining points with same vertical stress below ground level is called
Isobar.
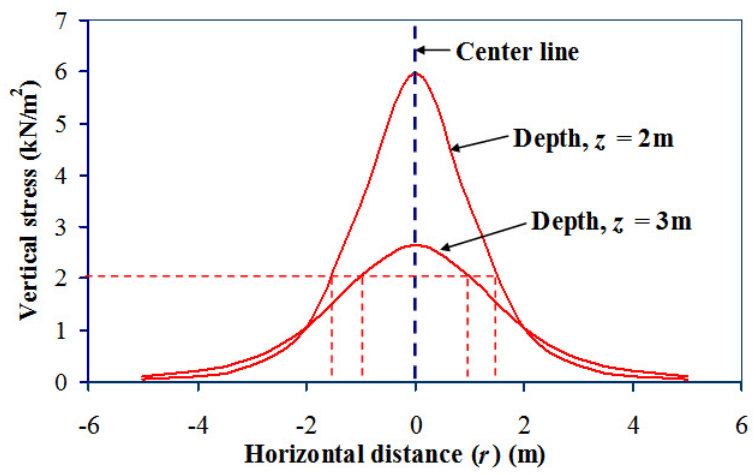
Fig.6.4. Variation of vertical stress with horizontal distance.
FAQs on Approximate Stress Distribution method - Stress in Soil due to applied load, Soil Mechanics - Soil Mechanics Notes- Agricultural Engineering
| 1. What is the approximate stress distribution method in soil mechanics? |  |
| 2. How does the approximate stress distribution method work in agricultural engineering? |  |
| 3. What are the factors considered in the approximate stress distribution method? |  |
| 4. How accurate is the approximate stress distribution method in predicting stress in soil? |  |
| 5. Can the approximate stress distribution method be used to analyze stress in different soil types? |  |















