Area formula
Area is the amount of space inside a two-dimensional shape. If you think about the floor of your bedroom, the area would be the maximum amount of floor you could throw your stuff on before you couldn't see any floor remaining.
Area is always expressed as square units (units2). This is because it is two-dimensional (length and height).
You can find the area of shapes by counting the boxes inside the shapes. In these three figures, each box represents 1 cm2.

- Figure A takes up 25 small boxes, so it has an area of 25 cm2
- Figure B takes up 36 small boxes, so it has an area of 36 cm2
- Figure C takes up 21 full boxes and 7 half boxes, so it has an area of

Area of Rectangle = Base x Height
Here is a 10 cm x 6 cm rectangle.

If we break it into section 1 cm wide, it would look like this:

Each row contains 10 squares and there are 6 rows, which gives a total of 10 × 6 square cm. That's the same as multiplying the base by the height: 6 x 10 = 60 cm2.
Area of Triangle = ½(Base × Height)
Here is a triangle with a base of 5 cm and a height of 6 cm.

If we place another triangle with the same height and base on top of this one, we get a 6 cm x 5 cm rectangle.

Now, we already know how to compute the area of a rectangle (base × height). So, the area of the rectangle is 5 cm x 6 cm = 30 cm2
However, we only want the triangle, which is half of the rectangle, 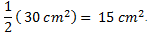 . Essentially we took ½ of the area of the whole rectangle, or ½ (base × height).
. Essentially we took ½ of the area of the whole rectangle, or ½ (base × height).
Area of Parallelogram = Base × Height
Now let's look at a parallelogram with a base of 6 cm and a height of 3 cm.

By moving the small triangle on the left all the way to the right, this shape becomes a rectangle with a base of 6 and a height of 3 cm.

Since you already know how to find the area of a rectangle (base × height), you have all the tools you need to find the area of this parallelogram.
Area of Trapezoid = ½(Base1 + Base2) x Height

Imagine cutting off the triangular lower left corner and fitting it onto the upper right corner like this:

Now, we just have another rectangle, but with a new base. The base of this new figure is the average of the original bases,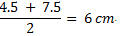 The area of this new figure is 6 cm x 3 cm = 18 cm2. Just be careful, because the base we are using is the mean of the two original bases!
The area of this new figure is 6 cm x 3 cm = 18 cm2. Just be careful, because the base we are using is the mean of the two original bases!
Area of Circle = πr2
Finally we will examine the beautiful circle. Here is one with a radius of 6 cm.

Here is the same circle but with lines drawn in at every cm.

First we combined the portions of square to make complete square, then we very carefully and diligently counted each and every one of those squares and found there to be approximately 113 squares. This is nearly equal to the 
Area Of Irregular Shapes
1. Find the area of this room:

This can be done in two different ways:
Method #1
| Method #2
|
Divide the figure into two rectangles and find all missing lengths.
| Draw two lines to make the figure into one large rectangle.
|
 |  |
The larger rectangle has an area of 
| The area of the large rectangle is  |
The smaller rectangle has an area of  | However, a  rectangle is not included in our original figure, so we need to take out the area of the white rectangle rectangle is not included in our original figure, so we need to take out the area of the white rectangle  |
If we combine these we will find the total area:  |  |
2. Find the area of this portion of a basketball court:

This figure is already divided into two shapes: a rectangle and half a circle.
We need to find the area of each and add them together.

3. A 20 foot x 12 foot pool is to be surrounded by a deck 6 feet in width. How many square feet of decking is needed to do this?
As always, we want to draw a picture of what this looks like.

The dimensions of the large outside rectangle are:

So, the area of the larger rectangle is 

The amount of decking we need is : 768 - 240 = 528 square feet!
Surface Area
Surface Area of a Cone = πr2 + πrs
To find the surface area of a cone, we need to find the area of the circular base and the area of the curved section. This one involves a new measurement, s, which is the length of the slanted part.

If you take apart the cone, you get two surfaces, the circular base, and the curved sides. The area of the base is just πr2, and the area of the curved section is πrs. So, the total surface area of a cone is πr2 +πrs.

Look Out: surface area is only two-dimensional and is expressed as units squared, not units cubed. This is because we are only dealing with the flat surfaces, not the inside space.






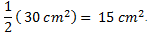 . Essentially we took ½ of the area of the whole rectangle, or ½ (base × height).
. Essentially we took ½ of the area of the whole rectangle, or ½ (base × height).



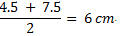 The area of this new figure is 6 cm x 3 cm = 18 cm2. Just be careful, because the base we are using is the mean of the two original bases!
The area of this new figure is 6 cm x 3 cm = 18 cm2. Just be careful, because the base we are using is the mean of the two original bases!








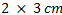 rectangle is not included in our original figure, so we need to take out the area of the white rectangle
rectangle is not included in our original figure, so we need to take out the area of the white rectangle 































