Argand Plane & Polar Representation | Mathematics for NDA PDF Download
Argand Plane
In the earlier classes, you read about the number line. It is a convenient way to represent real numbers as points on a line. Similarly, you read about the Cartesian Coordinate System. It is a set of three mutually perpendicular axes and a convenient way to represent a set of numbers (two or three) or a point in space.
Let us begin with the number line. Imagine that you are some kind of a mathematics god and you just created the real numbers. It so happened that you drew another line perpendicular to the real axis. What will this line be? It is definitely not real. Hence, it must be imaginary or the complex line.
Thus we have a way to represent any imaginary number graphically. All we need to do is find its real part and an imaginary part. Secondly, we represent them on the two mutually perpendicular number lines. The point of intersection, as shown above, is the origin of our Plane.
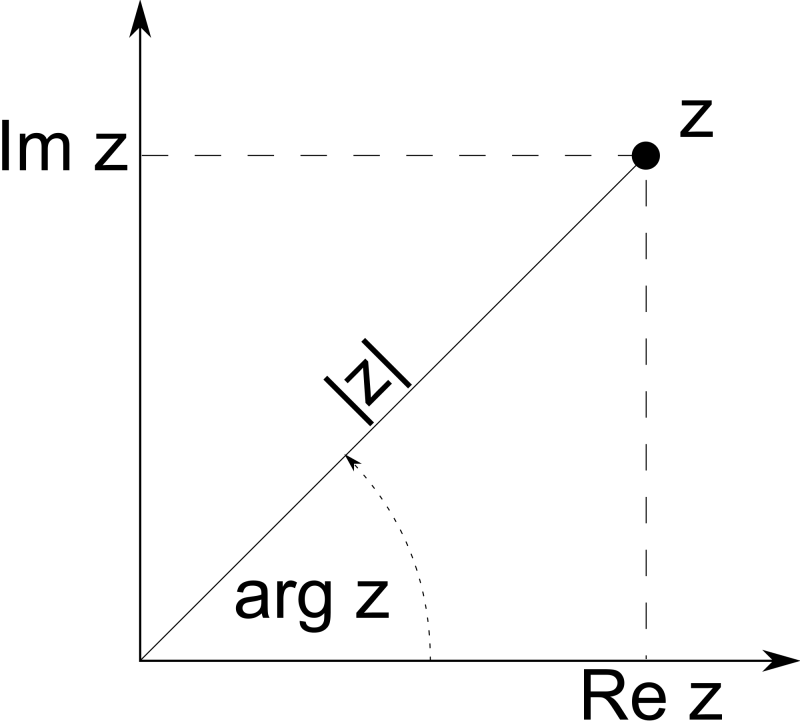
The Plane so formed is known as the Argand Plane and is a convenient way to represent any imaginary number graphically. Let z = x + iy. Then Re(z) = x and Im(z) = y.
The ordered pair (x,y) represented on the Argand plane will represent a point. This point corresponds to our complex number z. We draw a directed line from O to the point P(x,y) which represents z. Let θ be the angle that this line makes with the positive direction of the “Real Axis”. Therefore, (90 – θ) is the angle which it makes with the “Imaginary Axis”. This is somewhat important, so keep it handy!
Argument of z
As already established, every Complex number can be represented somewhere on the Argand Plane. This follows from the fact that under the operation of our Algebra, Complex numbers are closed. Imagine you represent two numbers, z1 = 2 +3i and z2 = 2 – 3i. We can see that |z1| = |z2|. Oops! What have we done? If you plot the two points (2, 3) and (2, -3), you will find they are symmetrical above and below the real axes. We call them the mirror images of each other.
How do we tell the difference between them? We introduce another quantity called the Argument of z1 and z2. It is defined as the angle ‘θ’ that the line joining the point P (representing our complex number) and the origin O, makes with the positive direction of the “Real Axes”. This gives each complex number a unique sense of a direction or orientation on the Argand Plane. Hence we can uniquely represent every point on the Argand Plane.
Modulus of A Complex Number
In an earlier section we defined the modulus of an imaginary number z = a + ib as |z| = 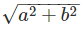 . Here we shall see that this definition fits perfectly with the geometrical representation of the complex numbers.
. Here we shall see that this definition fits perfectly with the geometrical representation of the complex numbers.
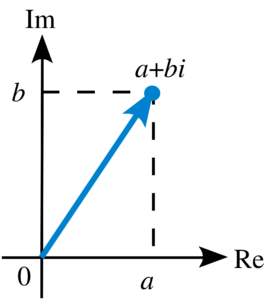
In the above figure, suppose the arrowhead is P (a, b), where P represents the number z = a + ib. Then the length of OP can be found out by using the distance formula as =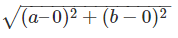
Hence we can say that OP = 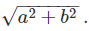 So the modulus is the length of the line segment joining the point, corresponding to our complex number, with the origin of the Argand Plane. As you can see it is always positive, hence we call it the modulus. It all falls into place now, doesn’t it?
So the modulus is the length of the line segment joining the point, corresponding to our complex number, with the origin of the Argand Plane. As you can see it is always positive, hence we call it the modulus. It all falls into place now, doesn’t it?
Polar Representation
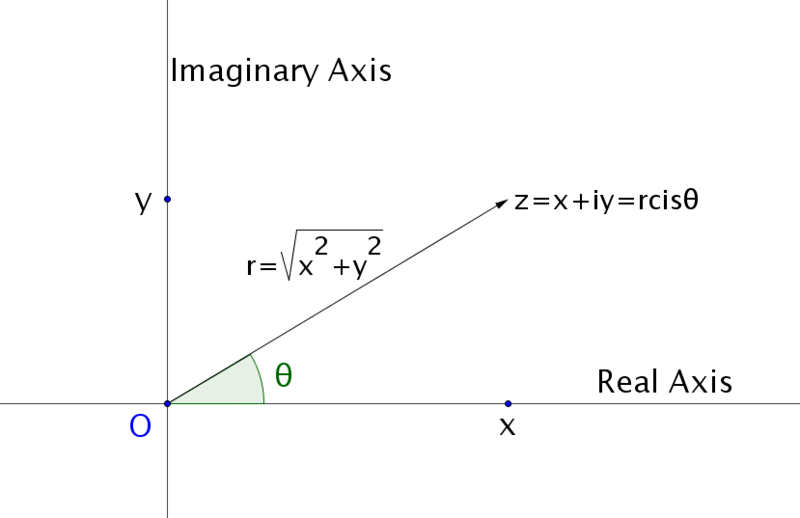
We have different types of Coordinate systems. One of them is the Polar Coordinate system. It is just a set of mutually perpendicular lines. The origin is called the Pole. We measure the position of any point by measuring the length of the line that connects it to the origin and the angle the line makes with a specified axis. For example, if we know the value of φ and r we can locate P. These are the polar coordinates, r and φ.Argument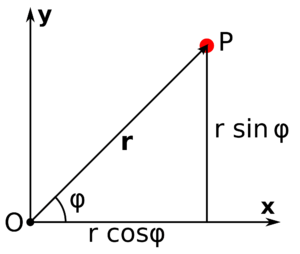
Similarly, if we know the Argument of a complex number in the Argand Plane and the length OP, we can locate the said number. Let r = OP. We also know that OP = |z| = r ; where z = x + iy
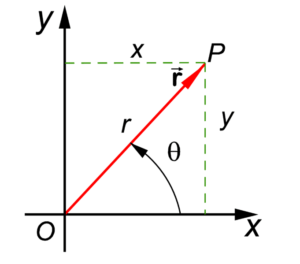
Argument: The coordinates of P are (x, y). In the right angled triangle we see that x = r cos(θ) and y = r sin(θ). So we can write, z = r cos(θ) + r sin(θ) = r [cos(θ) + sin(θ)]. This, my dear friends is the Polar representation of our complex number z = x + iy with:
Arg(z) = θ and |z| = r
Now y/x = r sin(θ)/r cos(θ) = tan θ
Therefore, θ = tan-1(y/x)
Using this relation, we can find the argument of a complex number.
Solved Examples For You
Q: If z = −2(1+2i)/(3 + i) where i= \( \sqrt[]{-1} \), then the argument θ(−π < θ ≤ π) of z is:
A) 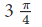
B) π/4
C)
D) 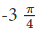
Solution: D) As z = −2(1+2i)/(3 + i)
Multiplying and dividing by (3 – i), we get
z = -2(1+2i)×(3 – i)/(3 + i)×(3 – i) = -1 – i
Comparing this to z = x + iy, we have x = -1 and y = -1
Therefore, θ = tan-1(y/x) = tan-1(1) = -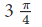
Why not π/4 ? Well because, both x and y are negative. This means that the point P is in the third quadrant now. Therefore, θ = -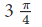 .
.
|
290 videos|298 docs|232 tests
|
FAQs on Argand Plane & Polar Representation - Mathematics for NDA
| 1. What is the Argand plane and how is it related to complex numbers? |  |
| 2. How is the polar representation of a complex number different from the Cartesian representation? |  |
| 3. How can the polar form of a complex number be converted into the Cartesian form? |  |
| 4. How can the Cartesian form of a complex number be converted into the polar form? |  |
| 5. What are the advantages of using the polar representation of complex numbers? |  |