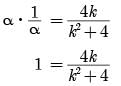Class 10 Maths Chapter 2 Assertion and Reason Questions - Polynomials
Q1: Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : x2 + 4x + 5 has two real zeroes.
Reason : A quadratic polynomial can have at the most two zeroes.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Ans: d
p(x) = 0 ⇒ x2 + 4x + 5 = 0
Discriminant, D = b2 – 4ac
= 42 – 4 x 1 x 5
= 16 – 20 = – 4 < 0
Therefore, no real zeroes are there.
Q2: Directions: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion: If the sum of the zeroes of the quadratic polynomial x2 - 2kx + 8 is 2 then value of k is 1.
Reason: Sum of zeroes of a quadratic polynomial ax2 + bx + c is - b/a
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Ans: a
Assertion (A): If the sum of the zeroes of the quadratic polynomial x2 - 2kx + 8 is 2, then the value of
k is 1.
Reason (R): The sum of the zeroes of a quadratic polynomial ax2 + bx + c is - (b/a).
Let's evaluate these statements:
For a quadratic equation ax2 + bx + c, the sum of the zeroes is given by - (b/a).
Given the quadratic polynomial x2 - 2kx + 8, if the sum of the zeroes is 2, then we have:
- (- 2k / 1) = 2
2k = 2
k = 1
So, both assertion (A) and reason (R) are true, and reason (R) correctly explains assertion (A).
Therefore, the correct choice is:
1. Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
Q3: Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion (A): If the zeroes of the quadratic polynomial (k – 1) x2 + kx + 1 is – 3, then the value of k is 4/3.
Reason (R): If – 1 is a zero of the polynomial p(x) = kx2 – 4x + k, then the value of k is –2.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Ans: b
In case of assertion:
Let p(x) = (k – 1)x2 + kx + 1
As –3 is a zero of p(x), then p (−3) = 0
⇒ (k – 1) (−3)2 + k (−3) + 1 = 0
⇒ 9k – 9 – 3k + 1 = 0
⇒ 9k – 3k = +9 – 1
⇒ 6k = 8
⇒ k = 4/3
∴ Given statement is correct.
In case of reason:
Since, – 1 is a zero of the polynomial and p(x) = kx2 – 4x + k, then p (–1) = 0
∴ k (–1)2 – 4 (–1) + k = 0
⇒ k + 4 + k = 0
⇒ 2k + 4 = 0
⇒ 2k = – 4
Hence, k = – 2
∴ Given statement is correct.
Thus, both assertion and reason are correct but reason is not the correct explanation for assertion.
Q4: Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : If one zero of poly-nominal p(x) = (k2 + 4)x2 + 13x + 4k is reciprocal of other, then k = 2.
Reason : If (x - α) is a factor of p(x), then p(α) = 0 i.e. α is a zero of p(x).
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Ans: b
Reason is true.Let α, 1/α be the zeroes of p(x), then
k2 - 4k + 4 = 0
(k - 2)2 = 0
k = 2 Assertion is true Since, Reason is not correct for Assertion.
Q5: Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : (2 - √3) is one zero of the quadratic polynomial then other zero will be (2 + √3).
Reason : Irrational zeros (roots) always occurs in pairs.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Ans: a
As irrational roots/zeros always occurs in pairs therefore, when one zero is (2 - √3) then other will be (2 + √3). So, both A and R are correct and R explains A.
Q6: Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : The graph y = f(x) is shown in figure, for the polynomial f(x). The number of zeros of f(x) is 3.
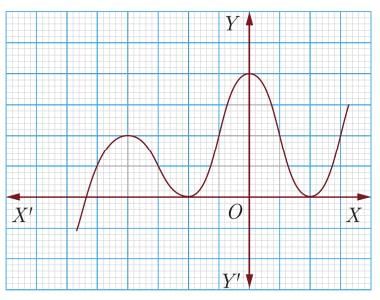
Reason : The number of zero of the polynomial f(x) is the number of point of which f(x) cuts or touches the axes.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Ans: c
As the number of zeroes of polynomial f(x) is the number of points at which f(x) cuts (intersects) the x –axis and number of zero in the given figure is 3.
So A is correct but R is not correct.
Q7: Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : P(x) = 14x3 - 2x2 + 8x4 + 7x - 8 is a polynomial of degree 3.
Reason : The highest power of x in the polynomial p(x) is the degree of the polynomial.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Ans: d
The highest power of x in the polynomial p(x)= 14x3 - 2x2 + 8x4 + 7x - 8x is 4.
Degree of p(x) is 4. So, A is incorrect but R is correct.
Q8: Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
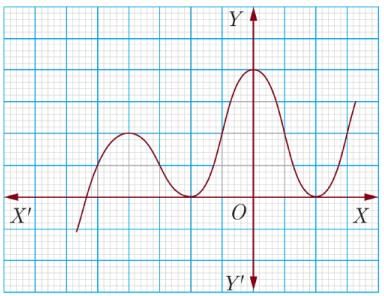
Assertion : The graph y = f(x) is shown in figure, for the polynomial f (x). The number of zeros of f(x) is 3.
Reason : The number of zero of the polynomial f(x) is the number of point of which f(x) cuts or touches the axes.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Ans: c
As the number of zeroes of polynomial f(x) is the number of points at which f(x) cuts (intersects) the x –axis and number of zero in the given figure is 3.So A is correct but R is not correct.
Q9: Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : Zeroes of f(x) = x2 - 4x - 5 are 5, - 1
Reason : The polynomial whose zeroes are 2 + √3, 2 - √3 is x2 - 4x + 7.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Ans: c
Zeroes of f(x) = x2 − 4x − 5 are obtained by solving:
x2 − 4x − 5 = 0, which implies
x2 − 5x + x − 5 = 0 or, x(x − 5) + 1(x − 5) = 0
which means x = 5 or x = −1
Thus the assertion is correct.
However, the reason is incorrect.
The numbers given are not the zeroes of x2 − 4x + 7
Q10: Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : x3 + x has only one real zero.
Reason : A polynomial of nth degree must have n real zeroes.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Ans: c
Reason is false [a polynomial of nth degree has at most x zeroes.] Again, x3 + x = x(x2 + 1)
which has only one real zero (x = 0)
[x2 + 1 ≠ 0 for all x ε R]
Assertion is true.
Q11: Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : If one zero of poly-nominal p(x) = (k2 + 4)x2 + 13x + 4k is reciprocal of other, then k = 2.
Reason : If (x – a) is a factor of p(x), then p(a) = 0 i.e. a is a zero of p(x).
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Ans: b
Let α, 1/α be the zeroes of p(x) then we have
Product of Zeroes
= a x (1/a) = 4k / (k2 + 4) = 1
⇒ k2 – 4k + 4 = 0
⇒ (k – 2)2 = 0 ⇒ k = 2
Q12: Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion: Degree of a zero polynomial is not defined.
Reason: Degree of a non-zero constant polynomial is 0
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Ans: b
We know that, the constant polynomial 0 is called a zero polynomial. The degree of a zero polynomial is not defined.So, Assertion is true. Now, the degree of a non-zero constant polynomial is zero. So, Reason is true.
Q13: Directions: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion: If the product of the zeroes of the quadratic polynomial x2 + 3x + 5k is -10 then value of k is -2.
Reason: Sum of zeroes of a quadratic polynomial ax2 + bx + c is -b/a
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Ans: b
Both the assertion and the reason are true, but the reason provided is related to the sum of the zeroes, not their product. The correct explanation involves the formula for the product of the zeroes of a quadratic polynomial, c/a, which would lead to 5k/−10, hence determining the value of k.
Q14: Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion: The sum and product of the zeros of a quadratic polynomial are -1/4 and 1/4 respectively.
Then the quadratic polynomial is 4x2 + x + 1.
Reason : The quadratic polynomial whose sum and product of zeros are given is x2-(sum of zeros). x + product of zeros.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Ans: a
Sum of zeros = -1/4 and product of zeros = 1/4
Quadratic polynomial be 4x2 + x + 1. So, both A and R are correct and R explains A.
Q15: Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : x2 + 7x + 12 has no real zeroes.
Reason : A quadratic polynomial can have at the most two zeroes.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Ans: d
x2 + 7x + 12 = 0⇒ x2 + 4x + 3x + 12 = 0
⇒ x(x + 4) + 3(x + 4) = 0
⇒ (x + 4) (x + 3) = 0
⇒ (x + 4) = 0 or (x + 3) = 0
⇒ x = −4 or x = −3
Therefore, x2 + 7x + 12 has two real zeroes.
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 2 Assertion and Reason Questions - Polynomials
| 1. What is a polynomial in mathematics? |  |
| 2. How do you classify polynomials based on their degree? |  |
| 3. What are the different operations that can be performed on polynomials? |  |
| 4. Can you explain the concept of the roots of polynomials? |  |
| 5. What is the significance of the Remainder Theorem in relation to polynomials? |  |