Detailed Notes: Averages | CSAT Preparation - UPSC PDF Download

Introduction

This chapter forms the backbone concept of most questions in the Quantitative Aptitude & Data Interpretation sections. This is a crucial chapter, & quick-solving methods in this concept will help you save time - which is an essential factor for your success.

Definition

Simple Average (or Mean) is defined as the ratio of the sum of the quantities to the number of quantities.

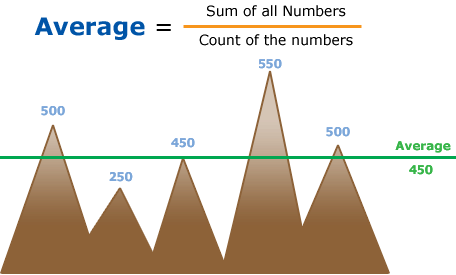Average Formula

Let us take a very simple example of the first five natural numbers 1, 2, 3, 4 & 5:

Now let’s add 2 more 3’s to these 5 numbers:

Here are a couple more examples of Simple Averages: 

Example 1: If a person with age 45 joins a group of 5 persons with an average age of 39 years. What will be the new average age of the group?

Sol: Total age will be 45 + 5× 39 = 240. And there will be 6 persons now.
So, the average will be 240/6 = 40.
(or)
Since, 45 is 6 more than 39, by joining the new person, the total will increase by 6 and so the average will increase by 1.
So, the average is 39 + 1 = 40.

Example 2:Two students with marks 50 and 54 leave class VIII A and move to class VIII B. As a result, the average marks of class VIII A fall from 48 to 46. How many students were there initially in class VIII A?

Sol: The average of all the students of class VIII A is 46, excluding these two students.
They have 4 and 8 marks more than 46. So, with the addition of these two students, 12 marks are adding more, and hence the average is increasing 2.
There should be 6 students in that class, including these two. This is the initial number of students

Weighted Average (or Weighted Mean)

• If somebody asks you to calculate the combined average marks of both the sections of class X, A and B when both sections have 60% and 70% average marks respectively? 
• Then your answer will be 65%, but this is wrong as you do not know the total number of students in each section. So to calculate the weighted average, we have to know the number of students in both sections.
• Let N₁, N₂, N₃, …. Nn be the weights attached to variable values X₁, X₂, X₃, …….. X_n respectively. Then the weighted arithmetic mean, usually denoted by:
  
• For any two different quantities taken in different ratios. The weighted average is just like a see-saw. 
  The more the ratio of a quantity, the more will be the inclination of the average from mid-value towards the value with more ratios.

Example 4: The average marks of 30 students in a section of class X are 20, while that of 20 students of the second section is 30. Find the average marks for the entire class X.

Sol: We can do the question by using both the Simple average & weighted average method.

Important Facts about Average

1. If each number is increased/decreased by a certain quantity n, then the mean also increases or decreases by the same quantity.
2. If each number is multiplied/ divided by a certain quantity n, then the mean also gets multiplied or divided by the same quantity.
3. If the same value is added to half of the quantities and the same value is subtracted from the other half quantities, then there will not be any change in the final value of the average.

Average Speed

• It is the total distance traveled divided by the time it takes to travel the distance.

• If d₁ & d₂ are the distances covered at speeds v₁ & v₂ respectively and the time taken are t₁ & t₂ respectively, then the average speed over the entire distance (x₁ + x₂) is given by:
  

  View Answer

• If both the distances are equal i.e. d₁ = d₂ = d then,   {i.e. Harmonic mean of two velocities}
• But if both the time taken are equal i.e. t₁ = t₂ = t then,
  Average speed =  {i.e. Algebraic mean of two velocities}

Example 5: The average of 10 consecutive numbers starting from 21 is:

Sol: The average is simply the middle number, which is the average of 5^th & 6^th no. i.e, 25 & 26 i.e. 25.5

Solved Examples

Example 1: A man travels 120 km at 60 km per hour and returns the same distance at 40 km per hour. What is his average speed for the entire journey?

Sol: The formula for average speed in a round trip is:

2 × Speed₁ × Speed₂Speed₁ + Speed₂

Here, Speed₁ = 60 km per hour and Speed₂ = 40 km per hour.

Using the formula:

2 × 60 × 4060 + 40 = 4800100 = 48 km per hour

Therefore , the answer to this question is 48 km per hour

Example 2: A grocer mixes two types of sugar. Type A costs ₹30 per kg, and Type B costs ₹50 per kg. How many kilograms of Type B sugar must he mix with 10 kg of Type A to get a mixture worth ₹40 per kg?

Sol:Let x be the quantity of Type B sugar in kg.

Using the weighted average formula:

30 × 10 + 50 × x10 + x = 40

Now, simplify the equation:

300 + 50x = 40 × (10 + x)

300 + 50x = 400 + 40x

Rearrange terms:

50x – 40x = 400 – 300

10x = 100

x = 10

Example 3: A company has three departments:

1. Department A has 10 employees with an average salary of ₹60,000.
2. Department B has 15 employees with an average salary of ₹80,000.
3. Department C has 5 employees with an average salary of ₹50,000.
   What is the overall average salary of all employees in the company?

Sol:First, calculate the total salary for each department:

Department A: 10 × 60,000 = 600,000

Department B: 15 × 80,000 = 1,200,000

Department C: 5 × 50,000 = 250,000

Now, sum all the salaries and divide by the total number of employees:

600,000 + 1,200,000 + 250,00010 + 15 + 5 = 2,050,00030 = 68,333.33

Answer: ₹68,333.33

Example 4: In an examination, the average mark of 4 girls and 6 boys is 24. Each of the girls has the same marks while each of the boys has the same marks. If the marks of any girl is at most double the marks of any boy, but not less than the marks of any boy, then the number of possible distinct integer values of the total marks of 2 girls and 6 boys is
(a) 20
(b) 19
(c) 21
(d) 22

Sol: 

Let the average marks of a boy and girl be b and g respectively.

Given, (4g + 6b)/10 = 24
=> 4g + 6b = 240
=> 2g + 3b = 120 …(1)

Also, b ≤ g ≤ 2b
=> 2b ≤ g ≤ 4b
=> 5b ≤ 2g ≤ 3b ≤ 7b …(2)

From (1) & (2), we get
5b ≤ 120 ≤ 7b
=> b ≤ 120/5 = 24 and b ≤ 17(1/7)

Now we need to find integral values of 2g + 6b
= 2g + 3b + 3b
= 120 + 3 * 120/7 ≤ 120 + 3b + 3 * 24 …from (3)
=> 171.42 < 120 + 3b < 192

Thus, the integral possible values of 2g + 6b are from 172 till 192 i.e., 21 possible integral values.Hence, option (c).
Hence, option (c).

Example 5: The average marks of 3 classes are as follows:

• Class A: 50 students with an average of 75.
• Class B: 30 students with an average of 80.
• Class C: 20 students with an average of 85.
  What is the overall average of all the students?

Sol:First, calculate the total marks for each class:

Class A: 50 × 75 = 3,750

Class B: 30 × 80 = 2,400
Class C: 20 × 85 = 1,700

Now, sum the total marks and the total number of students:

Total marks:

3,750 + 2,400 + 1,700 = 7,850

Total number of students:

50 + 30 + 20 = 100

The overall average is:

7,850100 = 78.5

Example 6: The average of three integers is 13. When a natural number n is included, the average of these four integers remains an odd integer. The minimum possible value of n is:
(a) 5
(b) 1
(c) 3
(d) 4

Sol:Sum of the original 3 numbers = 3 × 13 = 39.

Now, (39 + n) / 4 = odd = 2k - 1
=> 39 + n = 8k - 4
=> 43 + n = 8k
=> n = 8k - 43

For k to be an integer, the least possible natural value of n = 5.

Hence, option (a).