Banach Space:- Normed vector space | Additional Topics for IIT JAM Mathematics PDF Download
Definition:-
A Banach space is a vector space X over any scalar field K, which is equipped with a norm 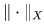 and which is complete with respect to the distance function induced by the norm, that is to say, for every Cauchy sequence {xn} in X, there exists an element x in X such that
and which is complete with respect to the distance function induced by the norm, that is to say, for every Cauchy sequence {xn} in X, there exists an element x in X such that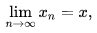
or equivalently: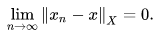
The vector space structure allows one to relate the behavior of Cauchy sequences to that of converging series of vectors. A normed space X is a Banach space if and only if each absolutely convergent series in X converges in X,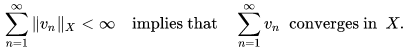
Completeness of a normed space is preserved if the given norm is replaced by an equivalent one.
All norms on a finite-dimensional vector space are equivalent. Every finite-dimensional normed space over R or C is a Banach space.
General theory:-
Linear operators, isomorphisms
If X and Y are normed spaces over the same ground field K, the set of all continuous K-linear maps T : X → Y is denoted by B(X, Y). In infinite-dimensional spaces, not all linear maps are continuous. A linear mapping from a normed space X to another normed space is continuous if and only if it is bounded on the closed unit ball of X. Thus, the vector space B(X, Y) can be given the operator norm
For Y a Banach space, the space B(X, Y) is a Banach space with respect to this norm.
If X is a Banach space, the space B(X) = B(X, X) forms a unital Banach algebra; the multiplication operation is given by the composition of linear maps.
If X and Y are normed spaces, they are isomorphic normed spaces if there exists a linear bijection T : X → Y such that T and its inverse T −1 are continuous. If one of the two spaces X or Y is complete (or reflexive, separable, etc.) then so is the other space. Two normed spaces X and Y are isometrically isomorphic if in addition, T is an isometry, i.e., ||T(x)|| = ||x|| for every x in X. The Banach–Mazur distance d(X, Y) between two isomorphic but not isometric spaces X and Y gives a measure of how much the two spaces X and Y differ.
Basic notions:- Every normed space X can be isometrically embedded in a Banach space. More precisely, for every normed space X, there exist a Banach space Y and a mapping T : X → Y such that T is an isometric mapping and T(X) is dense in Y. If Z is another Banach space such that there is an isometric isomorphism from X onto a dense subset of Z, then Z is isometrically isomorphic to Y.
This Banach space Y is the completion of the normed space X. The underlying metric space for Y is the same as the metric completion of X, with the vector space operations extended from X to Y. The completion of X is often denoted by 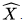
The cartesian product X × Y of two normed spaces is not canonically equipped with a norm. However, several equivalent norms are commonly used, such as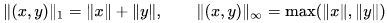
and give rise to isomorphic normed spaces. In this sense, the product X × Y (or the direct sum X ⊕ Y) is complete if and only if the two factors are complete.
If M is a closed linear subspace of a normed space X, there is a natural norm on the quotient space X / M,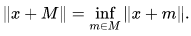
The quotient X / M is a Banach space when X is complete. The quotient map from X onto X / M, sending x in X to its class x + M, is linear, onto and has norm 1, except when M = X, in which case the quotient is the null space.
The closed linear subspace M of X is said to be a complemented subspace of X if M is the range of a bounded linear projection P from X onto M. In this case, the space X is isomorphic to the direct sum of M and Ker(P), the kernel of the projection P.
Suppose that X and Y are Banach spaces and that T ∈ B(X, Y). There exists a canonical factorization of T as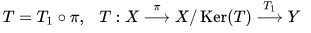
where the first map π is the quotient map, and the second map T1 sends every class x + Ker(T) in the quotient to the image T(x) in Y. This is well defined because all elements in the same class have the same image. The mapping T1 is a linear bijection from X / Ker(T) onto the range T(X), whose inverse need not be bounded.
Classical spaces:-
Basic examples of Banach spaces include: the Lp spaces and their special cases, the sequence spaces ℓp that consist of scalar sequences indexed by N; among them, the space ℓ1 of absolutely summable sequences and the space ℓ2 of square summable sequences; the space c0 of sequences tending to zero and the space ℓ∞ of bounded sequences; the space C(K) of continuous scalar functions on a compact Hausdorff space K, equipped with the max norm,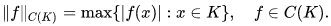
According to the Banach–Mazur theorem, every Banach space is isometrically isomorphic to a subspace of some C(K). For every separable Banach space X, there is a closed subspace M of ℓ1 such that X ≅ ℓ1/M.
Any Hilbert space serves as an example of a Banach space. A Hilbert space H on K = R, C is complete for a norm of the form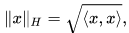
where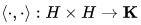
is the inner product, linear in its first argument that satisfies the following:
For example, the space L2 is a Hilbert space.
The Hardy spaces, the Sobolev spaces are examples of Banach spaces that are related to Lp spaces and have additional structure. They are important in different branches of analysis, Harmonic analysis and Partial differential equations among others.
Banach algebras:- A Banach algebra is a Banach space A over K = R or C, together with a structure of algebra over K, such that the product map A × A ∋ (a, b) ↦ ab ∈ A is continuous. An equivalent norm on A can be found so that ||ab|| ≤ ||a|| ||b|| for all a, b ∈ A.
Examples:-
- The Banach space C(K), with the pointwise product, is a Banach algebra.
- The disk algebra A(D) consists of functions holomorphic in the open unit disk D ⊂ C and continuous on its closure: D. Equipped with the max norm on D, the disk algebra A(D) is a closed subalgebra of C(D).
- The Wiener algebra A(T) is the algebra of functions on the unit circle T with absolutely convergent Fourier series. Via the map associating a function on T to the sequence of its Fourier coefficients, this algebra is isomorphic to the Banach algebra ℓ1(Z), where the product is the convolution of sequences.
- For every Banach space X, the space B(X) of bounded linear operators on X, with the composition of maps as product, is a Banach algebra.
- A C*-algebra is a complex Banach algebra A with an antilinear involution a ↦ a∗ such that ||a∗a|| = ||a||2. The space B(H) of bounded linear operators on a Hilbert space H is a fundamental example of C*-algebra. The Gelfand–Naimark theorem states that every C*-algebra is isometrically isomorphic to a C*-subalgebra of some B(H). The space C(K) of complex continuous functions on a compact Hausdorff space K is an example of commutative C*-algebra, where the involution associates to every function f its complex conjugate f .
Dual space:- If X is a normed space and K the underlying field (either the real or the complex numbers), the continuous dual space is the space of continuous linear maps from X into K, or continuous linear functionals. The notation for the continuous dual is X ′ = B(X, K) in this article. Since K is a Banach space (using the absolute value as norm), the dual X ′ is a Banach space, for every normed space X.
The main tool for proving the existence of continuous linear functionals is the Hahn–Banach theorem.
Hahn–Banach theorem. Let X be a vector space over the field K = R, C. Let further
- Y ⊆ X be a linear subspace,
- p : X → R be a sublinear function and
- f : Y → K be a linear functional so that Re( f (y)) ≤ p(y) for all y in Y.
Then, there exists a linear functional F : X → K so that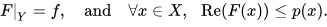
In particular, every continuous linear functional on a subspace of a normed space can be continuously extended to the whole space, without increasing the norm of the functional. An important special case is the following: for every vector x in a normed space X, there exists a continuous linear functional f on X such that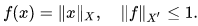
When x is not equal to the 0 vector, the functional f must have norm one, and is called a norming functional for x.
The Hahn–Banach separation theorem states that two disjoint non-empty convex sets in a real Banach space, one of them open, can be separated by a closed affine hyperplane. The open convex set lies strictly on one side of the hyperplane, the second convex set lies on the other side but may touch the hyperplane.
A subset S in a Banach space X is total if the linear span of S is dense in X. The subset S is total in X if and only if the only continuous linear functional that vanishes on S is the 0 functional: this equivalence follows from the Hahn–Banach theorem.
If X is the direct sum of two closed linear subspaces M and N, then the dual X ′ of X is isomorphic to the direct sum of the duals of M and N. If M is a closed linear subspace in X, one can associate the orthogonal of M in the dual,
The orthogonal M ⊥ is a closed linear subspace of the dual. The dual of M is isometrically isomorphic to X ′ / M ⊥. The dual of X / M is isometrically isomorphic to M ⊥.
The dual of a separable Banach space need not be separable, but:
Theorem. Let X be a normed space. If X ′ is separable, then X is separable.
When X ′ is separable, the above criterion for totality can be used for proving the existence of a countable total subset in X.
Weak topologies:-
The weak topology on a Banach space X is the coarsest topology on X for which all elements x ′ in the continuous dual space X ′ are continuous. The norm topology is therefore finer than the weak topology. It follows from the Hahn–Banach separation theorem that the weak topology is Hausdorff, and that a norm-closed convex subset of a Banach space is also weakly closed. A norm-continuous linear map between two Banach spaces X and Y is also weakly continuous, i.e., continuous from the weak topology of X to that of Y.
If X is infinite-dimensional, there exist linear maps which are not continuous. The space X∗ of all linear maps from X to the underlying field K (this space X∗ is called the algebraic dual space, to distinguish it from X ′) also induces a topology on X which is finer than the weak topology, and much less used in functional analysis.
On a dual space X ′, there is a topology weaker than the weak topology of X ′, called weak* topology. It is the coarsest topology on X ′ for which all evaluation maps x′ ∈ X ′ → x′(x), x ∈ X, are continuous. Its importance comes from the Banach–Alaoglu theorem.
Banach–Alaoglu Theorem. Let X be a normed vector space. Then the closed unit ball B ′ = {x′ ∈ X ′ : ||x′|| ≤ 1} of the dual space is compact in the weak* topology.
The Banach–Alaoglu theorem depends on Tychonoff's theorem about infinite products of compact spaces. When X is separable, the unit ball B ′ of the dual is a metrizable compact in the weak* topology.
Examples of dual spaces:-
The dual of c0 is isometrically isomorphic to ℓ1: for every bounded linear functional f on c0, there is a unique element y = {yn} ∈ ℓ1 such that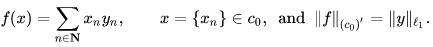
The dual of ℓ1 is isometrically isomorphic to ℓ∞. The dual of Lp([0, 1]) is isometrically isomorphic to Lq([0, 1]) when 1 ≤ p < ∞ and 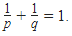
For every vector y in a Hilbert space H, the mapping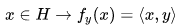
defines a continuous linear functional fy on H. The Riesz representation theorem states that every continuous linear functional on H is of the form fy for a uniquely defined vector y in H. The mapping y ∈ H → fy is an antilinear isometric bijection from H onto its dual H ′. When the scalars are real, this map is an isometric isomorphism.
When K is a compact Hausdorff topological space, the dual M(K) of C(K) is the space of Radon measures in the sense of Bourbaki. The subset P(K) of M(K) consisting of non-negative measures of mass 1 (probability measures) is a convex w*-closed subset of the unit ball of M(K). The extreme points of P(K) are the Dirac measures on K. The set of Dirac measures on K, equipped with the w*-topology, is homeomorphic to K.
Banach–Stone Theorem. If K and L are compact Hausdorff spaces and if C(K) and C(L) are isometrically isomorphic, then the topological spaces K and L are homeomorphic.
The result has been extended by Amir and Cambern to the case when the multiplicative Banach–Mazur distance between C(K) and C(L) is < 2. The theorem is no longer true when the distance is = 2.
In the commutative Banach algebra C(K), the maximal ideals are precisely kernels of Dirac mesures on K,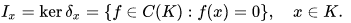
More generally, by the Gelfand–Mazur theorem, the maximal ideals of a unital commutative Banach algebra can be identified with its characters—not merely as sets but as topological spaces: the former with the hull-kernel topology and the latter with the w*-topology. In this identification, the maximal ideal space can be viewed as a w*-compact subset of the unit ball in the dual A ′.
Theorem. If K is a compact Hausdorff space, then the maximal ideal space Ξ of the Banach algebra C(K) is homeomorphic to K.
Not every unital commutative Banach algebra is of the form C(K) for some compact Hausdorff space K. However, this statement holds if one places C(K) in the smaller category of commutative C*-algebras. Gelfand's representation theorem for commutative C*-algebras states that every commutative unital C*-algebra A is isometrically isomorphic to a C(K) space. The Hausdorff compact space K here is again the maximal ideal space, also called the spectrum of A in the C*-algebra context.
Bidual:-
If X is a normed space, the (continuous) dual X ′′ of the dual X ′ is called bidual, or second dual of X. For every normed space X, there is a natural map,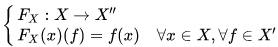
This defines FX(x) as a continuous linear functional on X ′, i.e., an element of X ′′. The map FX : x → FX(x) is a linear map from X to X ′′. As a consequence of the existence of a norming functional f for every x in X, this map FX is isometric, thus injective.
For example, the dual of X = c0 is identified with ℓ1, and the dual of ℓ1 is identified with ℓ∞, the space of bounded scalar sequences. Under these identifications, FX is the inclusion map from c0 to ℓ∞. It is indeed isometric, but not onto.
If FX is surjective, then the normed space X is called reflexive (see below). Being the dual of a normed space, the bidual X ′′ is complete, therefore, every reflexive normed space is a Banach space.
Using the isometric embedding FX, it is customary to consider a normed space X as a subset of its bidual. When X is a Banach space, it is viewed as a closed linear subspace of X ′′. If X is not reflexive, the unit ball of X is a proper subset of the unit ball of X ′′. The Goldstine theorem states that the unit ball of a normed space is weakly*-dense in the unit ball of the bidual. In other words, for every x ′′ in the bidual, there exists a net {xj} in X so that
The net may be replaced by a weakly*-convergent sequence when the dual X ′ is separable. On the other hand, elements of the bidual of ℓ1 that are not in ℓ1 cannot be weak*-limit of sequences in ℓ1, since ℓ1 is weakly sequentially complete.
Examples:-
A glossary of symbols:
- K = R, C;
- X is a compact Hausdorff space;
- I is a closed and bounded interval [a, b];
- p, q are real numbers with 1 < p, q < ∞ so that p /1+ q/1 = 1.
- Σ is a σ-algebra of sets;
- Ξ is an algebra of sets (for spaces only requiring finite additivity, such as the ba space);
- μ is a measure with variation |μ|.
Classical Banach spaces
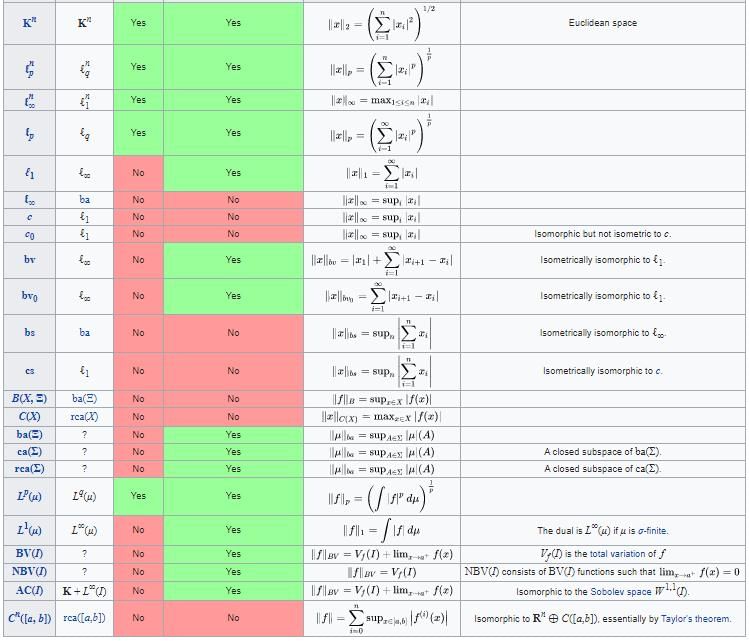
|
2 videos|45 docs|4 tests
|
FAQs on Banach Space:- Normed vector space - Additional Topics for IIT JAM Mathematics
| 1. What is a Banach space? |  |
| 2. What is the importance of completeness in a Banach space? |  |
| 3. How is a Banach space different from a normed vector space? |  |
| 4. What are some examples of Banach spaces? |  |
| 5. How are Banach spaces used in mathematical analysis? |  |
















