Banking of Road | Physics for JEE Main & Advanced PDF Download
| Table of contents |

|
| Turning on The Horizontal Roads |

|
| Banking of Road (without friction) |

|
| Banking of Road (with friction) |

|
| Solved Examples |

|
Turning on The Horizontal Roads
You must have seen the speed limit written just before taking a turn on these roads. Have you ever wondered how they calculate this speed limit? Let’s analyse the motion of a car taking a turn on a horizontal track.
Case1: If track is frictionless (μ = 0)
For a body to undergo circular motion centripetal force is necessary. On a frictionless horizontal track there is no centrifugal force. So we can not take a turn on a horizontal frictionless surface. Still we try to make a turn in that case the car will slip and get out of track.
Case2: Track is rough (μ ≠ 0)
In this case friction force will act as centripetal force. The frictional force is static in nature as there is no relative slipping. Let’s calculate maximum speed for the safe turn on horizontal circular rough surface whose coefficient friction is μs and radius is R. The direction of friction force will be inwards.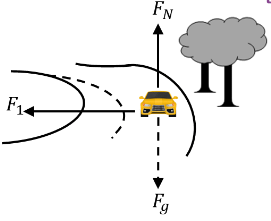
In vertical direction, Normal force is balanced with weight
So, N = mg
In horizontal direction,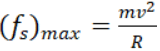
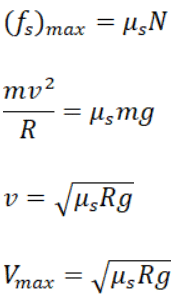
There the maximum speed for safe turn on horizontal track is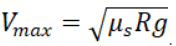
Banking of Road (without friction)
Banking of roads is the phenomenon in which the surface of a curved road is inclined with the horizontal to provide the necessary centripetal force for taking a safe turn.
Let a car of mass m moves with speed v along a curved road of the radius of curvature R, whose edges are raised by an angle θ with the horizontal. In this case the horizontal component of normal force will act as centripetal force. Look at the diagram given below.
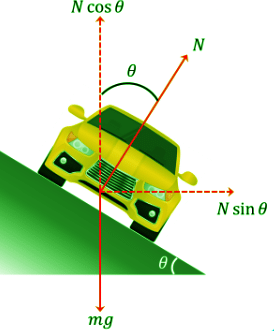 Balancing the forces in vertical direction, N cosθ = mg…..(1)
Balancing the forces in vertical direction, N cosθ = mg…..(1)
In horizontal direction net force towards centre is N sinθ
This net force towards centre act as centripetal force which is equal to mv2/R
Therefore, 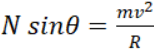 ………………………..(2)
………………………..(2)
By taking the ratio of equation (2) and (1), we get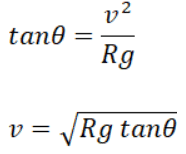
This is the safe speed of the car when the banked road is frictionless.
Note:
If the speed is more than the safe speed, then the car tends to skid outwards.
If the speed is less than the safe speed, then the car tends to skid inwards.
Banking of Road (with friction)
In this scenario the direction of friction will depend on the speed of the car. Because of that we get the range of safe speed. Let a car of mass m move with speed v along a curved road of radius of curvature R with banking angle θ. Since the friction force along the radial direction is a self-adjusting force, it increases or decreases with the speed of the car to avoid slipping. However, this friction has a maximum limit that is known as limiting friction.
Case1: Calculation of Maximum speed limit (Vmax)
The velocity of the car, corresponding to the limiting value of friction, is the maximum velocity with which a car can move without slipping. In this case the direction of friction will be downwards along the surface of the banked road because the car has the tendency to slip upward.
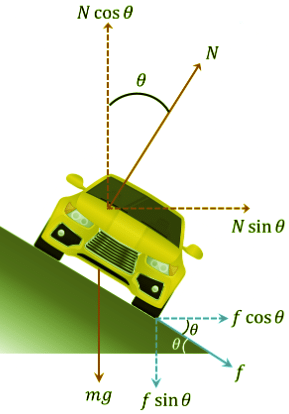
Balancing forces in vertical direction,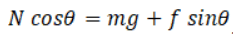 ...(1)
...(1)
In horizontal direction net force towards centre is N sinθ + f cosθ
This net force towards centre act as centripetal force which is equal to mv2max/R
Therefore 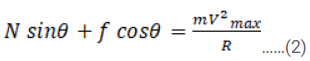
f = μN...... (3)
By solving these three equations we get,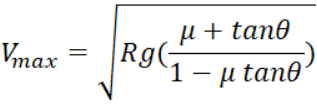
Case2: Calculation of Minimum speed limit (Vmin)
In this case the direction of friction will be upwards along the plane of the banked road as the car has a tendency to slip downward.
In this case the direction of friction will be upwards along the plane of the banked road as the car has a tendency to slip downward.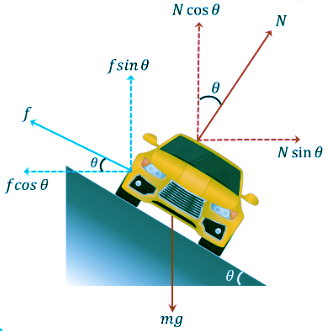 Balancing forces in vertical direction,
Balancing forces in vertical direction,
N cosθ + f sinθ = mg ....(1)
In horizontal direction net force towards centre is N sinθ - f cosθ
This net force towards centre act as centripetal force which is equal to 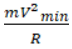
Therefore 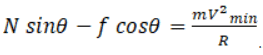 ....(2)
....(2)
f = μN ....(3)
By solving three equations we get,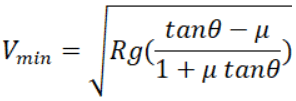
Solved Examples
Q.1. What should be the angle of banking of a circular track of radius 600m that is designed for cars with an average speed of 50ms-1?
Solution:
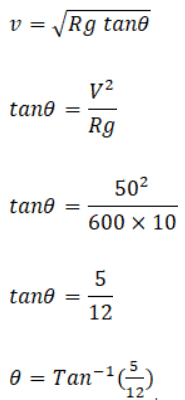
Q.2. A circular road of radius 40m has the angle of banking equal to 45º. At what speed should a vehicle go on this road so that the friction is not used?
Solution: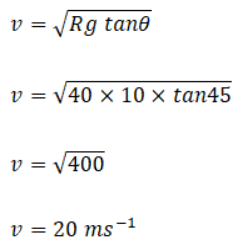
|
320 videos|994 docs|210 tests
|




















