Overview: Syllogism | General Aptitude for GATE - Mechanical Engineering PDF Download
| Table of contents |

|
| What is Syllogism? |

|
| Various Patterns of Premises |

|
| Method of Solving Syllogism Questions |

|
| Different Types of Questions |

|
| Solved Examples |

|
What is Syllogism?
Syllogism questions consist of a major and a minor premise, leading up to a conclusion. These questions ask you to derive the conclusion on the basis of the relationship existing between different elements of premises.
Let us see an example of syllogism:
Statements:
(a) All cats are dogs.
(b) All dogs are birds.
Conclusion: All cats are birds.
This conclusion is quite visible. But to solve complex problems we have some standard methods.
Various Patterns of Premises
A premise is something assumed or taken for granted.
Type 1: All As are Bs
Premise is: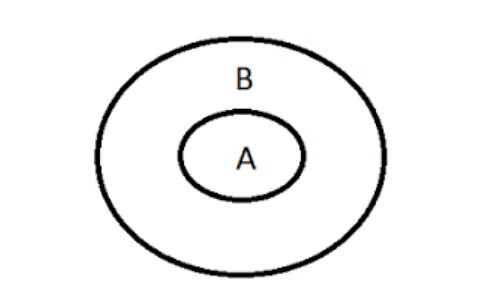
Reactions:
Some Bs are As- This is a definite conclusion.
Some Bs are not As- This is a probable conclusion.
Type 2: Some As are Bs
The premise is: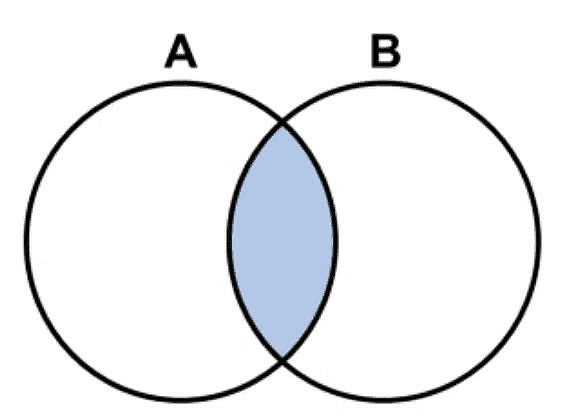
Valid Reactions: Some As are Bs - This is a definite conclusion (Although the above image also shows that some Bs are not As, this cannot be taken as a definite conclusion.)
Type 3: No A is B
The premise is as follows: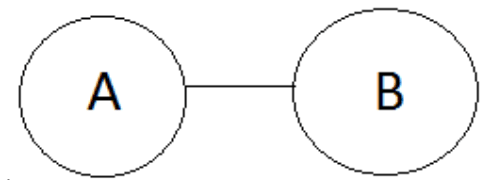 The conclusion No B is A is a valid conclusion.
The conclusion No B is A is a valid conclusion.
Type 4: Some As are not Bs
Premise: 
The first component has similarities with the second component.
Type 5: Only a Few
Premise: 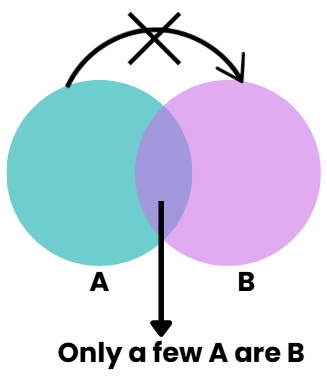
only a small portion of a group possesses a particular characteristic, not all of them.
Important Keywords to note:
1. Each, Every, Only, 100% → All
2. Almost, Little, Few, At most, At least, Many, Mostly, 1-99% → Some
3. None, 0% → No
Method of Solving Syllogism Questions
Method 1: Analytical Method
Following are the four major types of statements generally asked:
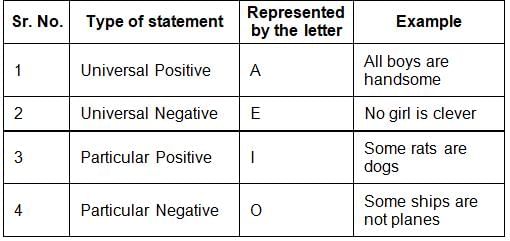
While deriving conclusions, the following points should be kept in mind:
- With two particular statements, no universal conclusion is possible.
- With two positive statements, no negative conclusion is possible.
- With two negative statements, no positive conclusion is possible.
- With two particular statements, no conclusion is possible, except when an 'I' type of statement is given and then by reversing it, an 'I' type of conclusion is given.
Important points related to conclusions drawn from single statements:
- A statement of type 'E' when reversed, gives a conclusion of type 'E & O'.
- A statement of type 'A' when reversed, gives a conclusion of type 'I'.
- A statement of type 'I' when reversed, gives a conclusion of type 'I.'
- A statement of type 'O' when reversed, does not give a conclusion of any type.
Method 2: Venn Diagrams
- Another method of solving such types of questions is by drawing a Venn diagram representing the statements.
- However, it is important that all possible Venn diagrams be drawn.
- If a conclusion can be deduced from all the possible solutions, then that conclusion is true.
- If the conclusion can be concluded from one of the possible Venn diagrams and not from the other possible Venn diagram, then that conclusion is taken as false.
Different Types of Questions
Type 1
There are two statements provided followed by two conclusions numbered I and II. You have to take the two given statements as true even if they seem to be at variance with commonly known facts. Decide which conclusion logically follows from given statement.
Q: Statements:
All roses are flowers.
Some flowers are red.
Conclusion:
I. Some roses are red.
II. All red things are roses.
Select the correct conclusion(s):
A) Only conclusion I
B) Only conclusion II
C) Both conclusions I and II
D) Neither conclusion I nor II
Ans: A) Only conclusion I
Explanation: Conclusion I is valid as it follows from the two statements (All roses are flowers, and some flowers are red). Conclusion II is not valid because we cannot infer that all red things are roses based on the given statements.
Type 2
There are three statements provided followed by four conclusions numbered I,II, III, IV. You have to take the two given statements as true even if they seem to be at variance with commonly known facts. Decide which conclusion logically follows from given statement.
Select the correct conclusion(s):
A) Only conclusion I and II
B) Only conclusion II
C) Only I and IV
D) Only II and IV
E) None
Q: Statements:
(a) Some apples are fruits
(b) All vegetables are fruits
(c) All fruits are vegetables
Conclusions
I. Some apples are vegetables
II. All vegetables are fruits
III. All fruits are apples
IV. Alll vegetables are apples.
Ans: (a)
Type 3
There are six statements followed by four options of combinations of any three of the given sentences. Choose the option in which the combinations are logically related.
A. All falcons fly high.
B. All falcons are blind.
C. All falcons are birds.
D. All birds are yellow.
E. All birds are thirsty.
F. All falcons are yellow.
Select the correct code:
(A) ABC
(B) CDF
(C) DEF
(D) BCA
Ans: (B)
Type 4
There are four arguments of three sentences each. Choose the set in which the third statement is a logical conclusion of the first two.
Question:
The following questions below contains four arguments of three sentences each. Choose the set in which the third statement is a logical conclusion of the first two.
A. Some icicles are cycles; all cycles are men; some icicles are men.
B. All girls have teeth; no teeth are yellow; no girls are yellows.
C. No hand is foot; some foot are heads; some heads are not hands.
D. Every man has a wife; All wives are devoted; no devoted has a husband.
(A) A only
(B) B only
(C)C only
(D) D only
Ans: Option (A) is the correct answer.
Solved Examples
Example 1: Which of the two conclusions can be concluded on the basis of given statements?
Statements:
- Some parrots are scissors.
- Some scissors are not combs.
Conclusions:
I. Some scissors are parrots.
II. Some combs are parrots.
Now, in this case, the possible conclusion is: Some scissors are parrots (I to I), as the universal principle no. 4 says, that with two particular statements only I to I is possible. Therefore, only 1 conclusion is possible. Nothing else is possible.
Venn diagram
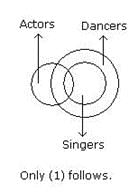
- Some actors are singers.
- All the singers are dancers.
Conclusions:
1. Some actors are dancers.
2. No singer is an actor.
Example 2: Which of the two conclusions can be concluded on the basis of given statements?
Statements:
- All flowers are candles.
- All lanterns are candles.
Conclusions:
I. Some flowers are lanterns.
II. Some candles are lanterns.
Three possible diagrams are shown above for the given statements.
Conclusion I follows from the last two possible solutions but does not follow from the first possible solution. Therefore, this conclusion is false.
Conclusion II follows from all the three possible solutions.
Therefore, conclusion II is true.
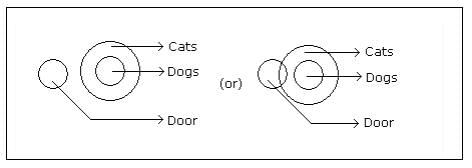
- No door is a dog.
- All the dogs are cats.
Conclusions:
(A) No door is a cat.
(B) No cat is a door.
(C) Some cats are dogs.
(D) All the cats are dogs.
Example 3: Which of the two conclusions can be concluded on the basis of given statements?
Statements:
- All prisoners are men.
- No man is educated.
Conclusions:
I. All prisoners are uneducated.
II. Some men are prisoners.
Two possible diagrams are shown below for the given statements.
Conclusion I follow from both the possibilities, so the conclusion I am true.
Conclusion II also follows from both the possibilities, so conclusion II is also true.
Therefore, both conclusions are true.
Example 4: Which of the two conclusions can be concluded on the basis of given statements?
Statements:
- All sides are lengths.
- No length is a breadth.
Conclusions:
I. All lengths are sides.
II. No breadth is aside.
Two possible diagrams are shown below for the given statements.
Conclusion I: False (conclusion follows from the second possibility but doesn't follow from the first possibility)
Conclusion II: True (conclusion follows from both the Venn diagram possibilities.)Therefore, only conclusion II is true.
Example 5:
Statements:
- All dogs are asses.
- All asses are bulls.
Conclusions:
- Some dogs are not bulls.
- Some bulls are dogs.
- All bulls are dogs.
- All dogs are bulls.
On the basis of both statements, the following one diagram is possible.
From the diagram it is clear that (2) and (4) conclusions logically follow.
Example 6:
Statements:
- All laptops are hills.
- Some laptops are cakes.
- Some cakes are hills.
- Some laptops are not cakes.
Conclusions:
- Only 1 follows.
- Only either II or IV follows.
- Only I and IV follows.
- Only I and III follows.
- None of these
From these given statements the following diagrams are possible
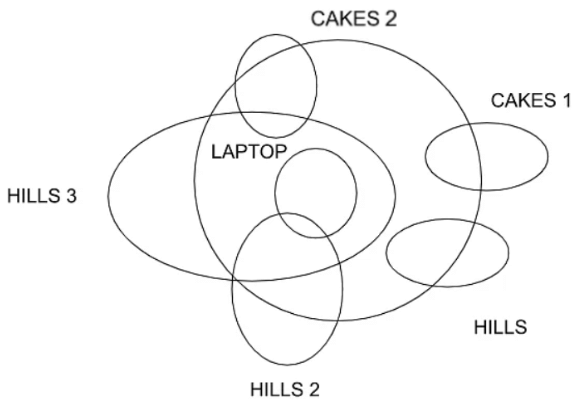
From the diagram neither (1) nor (2) conclusions follow.
Directions to Solve: In each of the following questions two statements are given and these statements are followed by two conclusions numbered (1) and (2). You have to take the given two statements to be true even if they seem to be at variance from commonly known facts. Read the conclusions and then decide which of the given conclusions logically follows from the two given statements, disregarding commonly known facts.
Give answer:
- (A) If only (1) conclusion follows
- (B) If sonly (2) conclusion follows
- (C) If either (1) or (2) follows
- (D) If neither (1) nor (2) follows and
- (E) If both (1) and (2) follow.
Example 7:
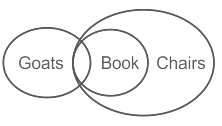
Statements:
- Some goats are books.
- All books are chairs.
Conclusions:
- Some books are chairs
- Some chairs are goats
A. Neither I nor II follow
B. Only II follows
C. Only I follows
D. Both I and II follow
E. Not Attempted
Correct Answer is Option (d)
The least possible Venn diagram is:
Conclusions:
I. Some books are chairs - Follows (As all books are chairs than some books will be chairs)
II. Some chairs are goats - Follows (As we know some goats are books and all books are chairs than some chairs will be goats)
Hence, the correct answer is "option (D)".
Example 8:
Statements: All the harmoniums are instruments. All the instruments are flutes.
Conclusions:
- All the flutes are instruments.
- All the harmoniums are flutes.
A. Only (1) conclusion follows
B. Only (2) conclusion follows
C. Either (1) or (2) follows
D. Neither (1) nor (2) follows
E. Both (1) and (2) follow
Correct Answer is Option (b)
Example 9:
Statements: Some mangoes are yellow. Some tixo are mangoes.
Conclusions:
- Some mangoes are green.
- Tixo is a yellow.
A. Only (1) conclusion follows
B. Only (2) conclusion follows
C. Either (1) or (2) follows
D. Neither (1) nor (2) follows
E. Both (1) and (2) follow
Correct Answer is Option (d)
Example 10:
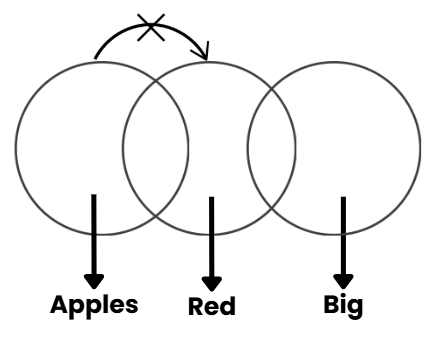
Statements: Only a few apples are red., Some red things are big.
Conclusions:
- Some apples are big.
- Some big things are apples.
A. Only (1) conclusion follows
B. Only (2) conclusion follows
C. Either (1) or (2) follows
D. Neither (1) nor (2) follows
E. Both (1) and (2) follow
Answer: A) Only conclusion I
Explanation:
Conclusion I is true because a few apples are red, and some red things are big, so it's possible that some apples could be big.
Conclusion II is not valid because the premises don’t support that some big things must be apples.
|
229 videos|191 docs|158 tests
|
FAQs on Overview: Syllogism - General Aptitude for GATE - Mechanical Engineering
| 1. What is syllogism? |  |
| 2. What are the various patterns of premises in syllogism? |  |
| 3. What is the analytical method of solving syllogism questions? |  |
| 4. What is the method of solving syllogism questions using Venn diagrams? |  |
| 5. What are some frequently asked questions related to syllogism in bank exams? |  |