Basic Concepts in Mechanics - Civil Engineering (CE) PDF Download

Introduction 


Before venturing into the generalization of these concepts and equations,

INTRODUCTION

a few drawbacks of the definitions and ideas that one might have acquired from the previous course needs to be highlighted and clarified. This we shall do in sections 1.1 and 1.2. Specifically, in section 1.1 we look at the four concepts in mechanics and in section 1.2 we look at the equations in mechanics. These sections also serve as a motivation for the mathematical tools that we would be developing in chapter 2. Then, in section 1.3 we look into various idealizations of the response of materials and the mathematical framework used to study them. However, in this course we shall be only focusing on the elastic response or more precisely, non-dissipative response of the materials. Finally, in section 1.4 we outline three ways by which we can solve problems in mechanics.

Basic Concepts in Mechanics 
What is force?

Force is a mathematical idea to study the motion of bodies. It is not “real” as many think it to be. However, it can be associated with the twitching of the muscle, feeling of the burden of mass, linear translation of the motor, so on and so forth. Despite seeing only displacements we relate it to its cause the force, as the concept of force has now been ingrained.
Let us see why force is an idea that arises from mathematical need. Say, the position¹ (x_o) and velocity (v_o) of the body is known at some time, t = t_o, then one is interested in knowing where this body would be at a later time, t = t_1. It turns out that mathematically, if the acceleration (a) of the body at any later instant in time is specified then the position of the body can be determined through Taylor’s series. That is if
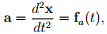                                 (1.1) 
then from Taylor’s series
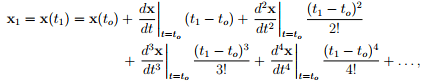       (1.2)

which when written in terms of x_o, v_o and a reduces to²
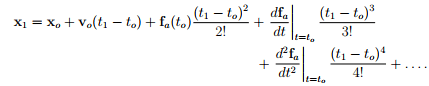     (1.3)
Thus, if the function f_a is known then the position of the body at any other instant in time can be determined. This function is nothing but force per unit mass³ , as per Newton’s second law which gives a definition for the force. This shows that force is a function that one defines mathematically so that the position of the body at any later instance can be obtained from knowing its current position and velocity.

It is pertinent to point out that this function f_a could also be prescribed using the position, x and velocity, v of the body which are themselves function of time, t and hence fa would still be a function of time. Thus, f_a = g(x(t), v(t), t). However, f_a could not arbitrarily depend on t, x and v. At this point it suffices to say that the other two laws of Newton and certain objectivity requirements have to be met by this function. 

Next, let us understand what kind of quantity is force. In other words is force a scalar or vector and why? Since, position is a vector and acceleration is second time derivative of position, it is also a vector. Then, it follows from equation (1.1) that f_a also has to be a vector. Therefore, force is a vector quantity. Numerous experiments also show that addition of forces follow vector addition law (or the parallelogram law of addition). 

As a summary, we showed that force is a mathematical construct which is used to mathematically describe the motion of bodies.

What is stress? 
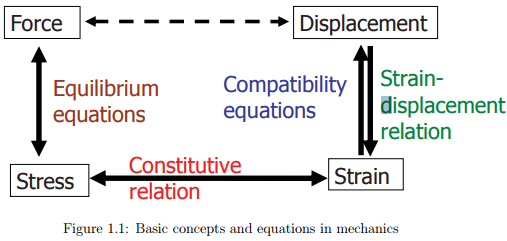
As is evident from figure 1.1, stress is a quantity derived from force. The commonly stated definitions in an introductory course in mechanics for stress are:
1. Stress is the force acting per unit area
2. Stress is the resistance offered by the body to a force acting on it

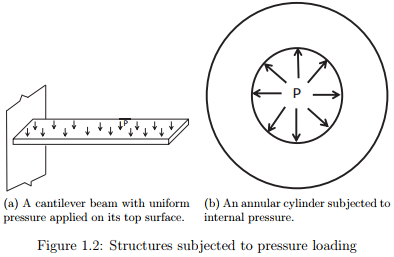
While the first definition tells how to compute the stress from the force, this definition holds only for simple loading case. One can construct a number of examples where definition 1 does not hold. The following two cases are presented just as an example. Case -1: A cantilever beam of rectangular cross section with a uniform pressure, p, applied on the top surface, as shown in figure 1.2a. According to the definition 1 the stress in the beam should be p, but it is not. Case -2: An annular cylinder subjected to a pressure, p at its inner surface, as shown in figure 1.2b. The net force acting on the cylinder is zero but the stresses are not zero at any location. Also, the stress is not p, anywhere in the interior of the cylinder. This being the state of the first definition, the second definition is of little use as it does not tell how to compute the stress. These definitions does not tell that there are various components of the stress nor whether the area over which the force
  
is considered to be distributed is the deformed or the undeformed. They do not distinguish between traction (or stress vector), t(_n) and stress tensor, σ.

Traction is the distributed force acting per unit area of a cut surface or boundary of the body. This traction apart from varying spatially and temporally also depends on the plane of cut characterized by its normal. This quantity integrated over the cut surface gives the net force acting on that surface. Consequently, since force is a vector quantity this traction is also a vector quantity. The component of the traction along the normal direction⁴ , n is called as the normal stress (σ(_n)). The magnitude of the component of the traction⁵ acting parallel to the plane is called as the shear stress (τ(_n)).

If the force is distributed over the deformed area then the corresponding traction is called as the Cauchy traction (t(n)) and if the force is distributed over the undeformed or original area that traction is called as the Piola traction (p(_n)). If the deformed area does not change significantly from the original area, then both these traction would have nearly the same magnitude and direction. 

4 Here n is a unit vector. 5Recognize that there would be two components of traction acting on the plane of cut. Shear stress is neither of those components. For example, if traction on a plane whose normal is ez is, t(ez) = axex + ayey + azez, then the normal stress σ(ez) = az and the shear stress τ(ez) = 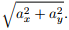 See chapter 4 for more details.

The stress tensor, is a linear function (crudely, a matrix) that relates the normal vector, n to the traction acting on that plane whose normal is n. The stress tensor could vary spatially and temporally but does not change with the plane of cut. Just like there is Cauchy and Piola traction, depending on over which area the force is distributed, there are two stress tensors. The Cauchy (or true) stress tensor, σ and the Piola-Kirchhoff stress tensor (P). While these two tensors may nearly be the same when the deformed area is not significantly different from the original area, qualitatively these tensors are different. To satisfy the moment equilibrium in the absence of body couples, Cauchy stress tensor has to be symmetric tensor (crudely, symmetric matrix) and Piola-Kirchhoff stress tensor cannot be symmetric. In fact the transpose of the Piola-Kirchhoff stress tensor is called as the engineering stress or nominal stress. 

What is displacement? 
The difference between the position vectors of a material particle at two different instances of time is called as displacement. In general, the displacement of the material particle would depend on time; the instances between which the displacement is sought. It is also possible that different particles get displaced differently between the same two instances of time. Thus, displacement in general varies spatially and temporally. Displacement is what can be observed and measured. Forces, traction and stress tensors are introduced to explain (or mathematically capture) this displacement.

The displacement field is at least differentiable twice temporally so that acceleration could be computed. This stems from the observations that the location or velocity of the body does not change abruptly. Similarly, the basic tenant of continuum mechanics is that the displacement field is continuous spatially and is piecewise differentiable spatially at least twice. That is while the displacement field is required to be continuous over the entire body it is required to be twice differentiable not necessarily over the entire body but only on subsets of the body. Thus, in continuum mechanics interpenetration of two surfaces or separation and formation of new surfaces is precluded. The validity of the theory stops just before the body fractures. Notwithstanding this many attempt to use continuum mechanics concepts to understand the process of fracture.

A body is said to undergo rigid body displacement if the distance between any two particles that belongs to the body remains unchanged. That is in a rigid body displacement the particles that belong to a body do not move relative to each other. A body is said to be rigid if it always undergoes only rigid body displacement under action of any force. On the other hand, a body is said to be deformable if it allows relative displacement of its particles under the action of some force. Though, all real bodies are deformable, at times one could idealize a given body as rigid under the action of certain forces.

What is strain? 
One observes that rigid body displacements of the body does not give raise to any stresses. Further, stresses are induced only when there is relative displacement of the material particles. Consequently, one requires a measure (or metric) for this relative displacement so that it can be related to the stress. The unique measure of relative displacement is the stretch ratio, λ(A) , defined as the ratio of the deformed length to the original length of a material fiber along a given direction, A. (Note that here A is a unit vector.) However, this measure has the drawback that when the body is not deformed the stretch ratio is 1 (by virtue of the deformed length being same as the original length) and hence inconvenient to write the constitutive relation of the form
σ_(A) = f(λ_(A)),                                   (1.4)

where σ_(A) denotes the normal stress on a plane whose normal is A. Since the stress is zero when the body is not deformed, the function f should be such that f(1) = 0. Mathematical implementation of this condition that f(1) = 0 and that f be a one to one function is thought to be difficult when f is a nonlinear function of λ_(A) . Consequently, another measure of relative displacement is sought which would be 0 when the body is not deformed and less than zero when compressed and greater than zero when stretched. This measure is called as the strain, ∈_(A) . There is no unique way of obtaining the strain from the stretch ratio. The following functions satisfy the requirement of the strain:
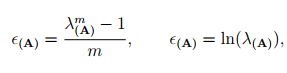                                   (1.5)
where m is some real number and ln stands for natural logarithm. Thus, if m = 1 in (1.5a) then the resulting strain is called as the engineering strain, if m = −1, it is called as the true strain, if m = 2 it is Cauchy-Green strain. The second function wherein ∈_(A) = ln(λ_(A)), is called as the Hencky strain or the logarithmic strain.

Just like the traction and hence the normal stress changes with the orientation of the plane, the stretch ratio also changes with the orientation along which it is measured. We shall see in chapter 3 that a tensor called the Cauchy-Green deformation tensor carries all the information required to compute the stretch ratio along any direction. This is akin to the stress tensor which when known we could compute the traction or the normal stress in any plane.