Basic Integration- I | Mathematics for Competitive Exams PDF Download
Antiderivatives - Differentiation in Reverse
Consider the function F(x) = 3x2 + 7x - 2. Suppose we write its derivative as f(x), i.e. f(x) = dF/dx. We already know how to find this derivative by differentiating term by term to obtain f(x) = dF/dx = 6x + 7. This process is illustrated in Fig..

Suppose now that we work back to front and ask ourselves which function or functions could possibly have 6x + 7 as a derivative. Clearly, one answer to this question is the function 3x2 + 7x - 2. We say that F(x) = 3x2 + 7x - 2 is an antiderivative of f(x) = 6x + 7.
There are however other functions which have derivative 6x + 7. Some of these are
3x2 + 7x + 3, 3x2 + 7x, 3x2 + 7x - 11
The reason why all of these functions have the same derivative is that the constant term disappears during differentiation. So, all of these are antiderivatives of 6x + 7. Given any antiderivative of f(x), all others can be obtained by simply adding a different constant. In order words, if F(x) is an antiderivative of f(x), then so too is F(x) + C for any constant C.
Geometrical Interpretation of Integration
Let f(x) be a given continuous function and F(x) one of its antiderivatives such that
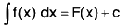
if 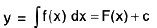
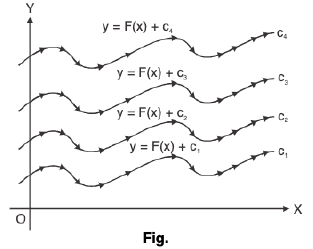
then y = F(x) + c represents a family of “parallel” curves.
It is clear from (1), we have
Here c4 > c3 > c2 > c, > 0.
Integral curve of the equation dy = dx.
Given dy = dx
Comparing (1) with dy = f(x) dx
∴ f(x) = 1
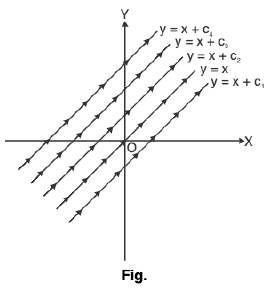
or 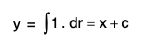
the integral curves are parallel lines with slope of all arrows is unity.
Example 1 : Find the integral curve of the equation dy = 2x dx.
Given dy = 2x dx ..........(1)
Comparing (1) with dy = f(x) dx
∴ f(x) = 2x
or

represents a family of “parallel” curves.
Example :
(a) Differentiate F(x) = 4x3 - 7x2 + 12x - 4 to find f(x) = dF/dx .
(b) Write down several antiderivatives of f(x) = 12x2 - 14x + 12.
(a) Differentiating F(x) = 4x3 - 7x2 + 12x - 4 we find f(x) = dF/dx = 12x2 - 14x + 12. We can deduce from this that an antiderivative of 12x2 - 14x + 12 is 4x3 - 7x2 + 12x - 4.
(b) All other antiderivatives of f(x) will take the form F(x) + C where C is a constant. So, the following are all antiderivatives of f(x):
4x3 - 7x2 + 12x - 4, 4x3 - 7x2 + 12x - 10, 4x3 - 7x2 + 12x, 4x3 - 7x2 + 12x + 3
From these examples we deduce the following important observation.
A function F(x) is an antiderivative of f(x) if dF/dx = f(x).
If F(x) is an antiderivative of f(x) then so too is F(x) + C for any constant C.
Derivatives
(i) 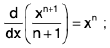
Particularly, we note that d/dx(x) = 1;
(ii) 
(iii) 
(iv) 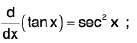
(v) 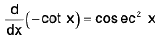
(vi) 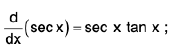
(vii) 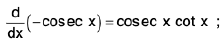
(viii) 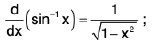
(ix) 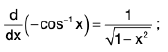
(x) 
(xi) 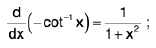
(xii) 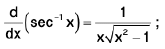
(xiii) 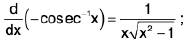
(xiv) 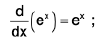
(xv) 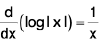
(xvi) 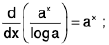
Integrals (Anti derivatives)
(i) 
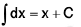
(ii) 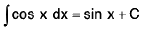
(iii) 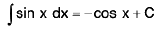
(iv) 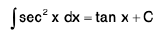
(v) 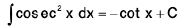
(vi) 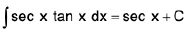
(vii) 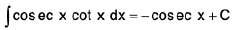
(viii) 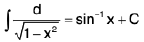
(ix) 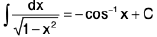
(x) 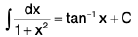
(xi) 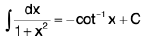
(xii) 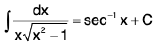
(xiii) 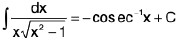
(xiv) 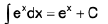
(xv) 
(xvi) 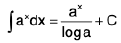
Example 2 : Let I = 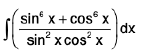
=
=
=
=
=
= tan x - cot x - 3x + c
Example 3 : Let I =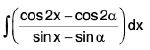
=
=
=
=
=
= = 2 cos x - 2x sin α + c
Example 4 : Evaluate :
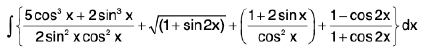
Let I =
=
=
=
=
Properties of the Indefinite Integral
The differential of an indefinite integral is equal to the element of integration, and the derivative of an indefinite integral is equal to the integral.
Thus, we have d ∫f ( x ) dx = f( x ) dx
or 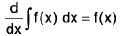 or
or 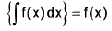
e.g. 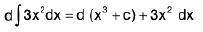
or 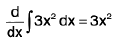
The indefinite integral of the differential of a continuously differentiable function is equal to this function, but introduces an arbitrary additive constant.
Thus, we have ∫df(x) = f(x) + c
e.g., ∫d cosx = cosx + c
A non-zero constant factor may be taken outside the sign of the integral, i.e., if constant a ≠ 0 , then
∫a f (x) dx = a∫f ( x ) dx
e.g., 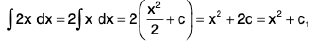
where c1 + 2c
The integral of an algebraic sum is equal to the sum of the integrals of the summands for n summands:
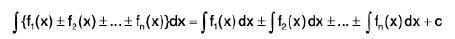
e.g., 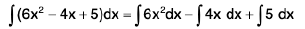
= 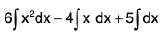
= 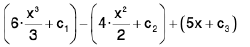
= 2x3 - 2x2 + 5x + c
where c = c1 - c2 + c3 Note : The constant term for every integral is adjoined in the last after all integrations have been performed.
Methods of Integration
To find the integral of complex problems (The integral is not a derivative of a known function). Following methods are used.
(I) Integration by Substitution or by change of the independent variable : If the independent variable x in ∫f(x) dx be changed to a new variable t, then we substitute x = ∅(t), where ∅(t) is a continuous differentiable function, then
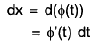
then we have
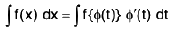
which is either a standard form or is easier to integrate. Here after integration we revert back to the old variable x by the inverse substitution t = ∅-1(x).
(a) Three fundamental deductions of the method of substitution :
Deduction I : 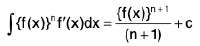 (n ≠ 1)
(n ≠ 1)
Deduction II :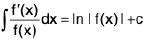
Deduction III : 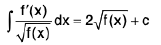
(b) Standard Substitutions :

(c) Extended forms of fundamental formulae :
if ∫f(x)dx = F(x) then we find ∫f(ax + b)dx.
Let I = ∫f(ax + b)dx ...(1)
Putting ax + b = t so that a dx = dt ⇒ 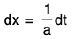
then I = 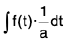
= 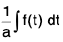
= 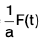 [ ∴∫f(t) dt = F(t)]
[ ∴∫f(t) dt = F(t)]
= 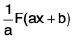 .....(2)
.....(2)
From (1) and (2) we get
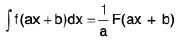
Thus to evaluate ∫f(ax + b)dx supposing in mind ax + b as a variable like x and divide it by the coefficient of x in ax + b i.e., a.
From this we obtain the following results :
(i) 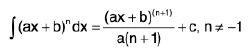
(ii) 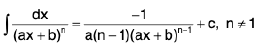
(iii) 
(iv) 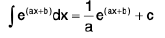

Example 5 : Evaluate : 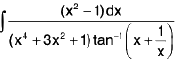
Let I =
=
=
Put x + 1/x = t
Again put tan-1 t = z
⇒
then we get
I =
[∴ z = tan-1 t]
=
Example 6 : Evaluate :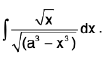
Let I =
Since integral of
then put x3/2 = t ⇒ x3 = t2
or
then we get I =
=
=
=
=
II. Integration by Parts
Let u and v be two functions of x, then we know that from differential calculus
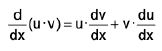
Integrating both sides w. r. t. x, we get

or 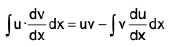 .............(1)
.............(1)
Now put u = f(x) and v = ∫g(x) dx,
so that 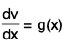
Substituting these value in (1), we get
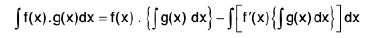
The above formula can be put in words i.e., The integral of the product of two functions =(first function) * (integral of the second function) - Integral of {diff. coeff. of the first function x Integral of the second function}
How to Choose 1st and 2nd function
(i) If the two functions are of different types take that function as 1st which comes first in the word I LATE where I stands for inverse Trigonometric function, L stands for logarithmic function, A stands for algebraic function, T stands for trigonometric function and E stands for exponential function.
(ii) If both functions are algebraic take that function as 1st whose differential coefficient is simpler, and take remaining as the 2nd function.
(iii) If both function are trigonometrical take that function as 2nd whose integral is simpler and take remaining as the 1st function.
(iv) If integral contains only one function which can not be directly integral.
(i.e., ln I x I, sin-1 x, cos-1 x, tan -1 x, ... etc.) then second function be chosen as unity.
Note : The formula of integration by parts can be applied more than once if necessary.
Example 7 : Evaluate :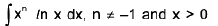
Let I =
Here xn is algebraic and /n x is logarithmic function, in ILATE rule L come before A, therefore Integrating by parts taking xn as second function, we have
=
=
=
Example 8 : Evaluate : ∫sin -1 x d x .
Let I = ∫sin -1 x d x .
Here there is only one function which can not be directly integrated then unity should be taken as the 2nd function we have
I = ∫sin -1 x 1. d x .
=
=
In integral put 1 - x2 = t
⇒ x dx = -1/2dt
then I =
=
=
(∵t = 1 - x2)
Note : Remember
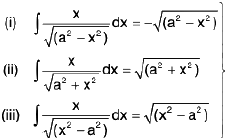
Cancellation of Integrals
Sometimes we split the integrand into the sum of two parts such that the integration of one of them by parts cancels the other.
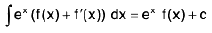
Proof : 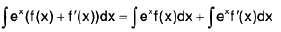
Integrating 1st term by parts taking ex as second function we have
= 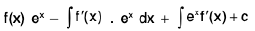
= ex f(x) + c (The last two integrals cancel each other).
Alternative Proof :
∴ 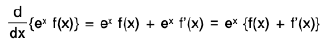
On integrating both sides, we have
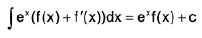
Note :
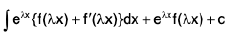
This is every important and the students can use this as a formula.
Example 9 : Evaluate :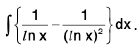
Let I =
Put ln x = t ⇒ x = et ⇒ dx = etdt
then
=
=
where f(t) = 1/t and f’(t) = -1/t2
∴
Note : If logarithmic function or inverse circular function presents in the denominator of integrand
i.e., 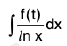 or
or 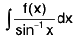
then put it equal to t.
Integrals of eaxcos bx and eaxsin bx :
Prove : 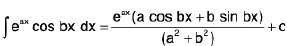
and 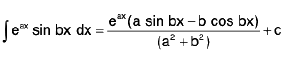
Proof : Let I = 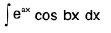 . ....(1)
. ....(1)
Integrating by parts taking eax as 2nd function, we have
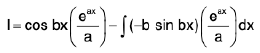
= 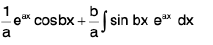 . ....(2)
. ....(2)
Again integrating by parts taking eax as 2nd function, then
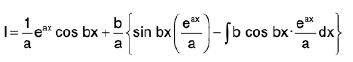
= 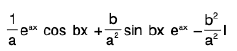 (from (1))
(from (1))
or 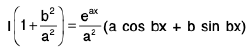
⇒ 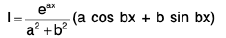
Example 10 : Evaluate :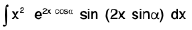
Let I =
where a = 2 cos α and b = 2 sin α
∴
= 2
and
......(1)
Integrating by parts
We know that
Let I1 =
=
=

=
=

Now, Let l2 =
Now substituting a = 2 cos α and b = 2 sin α in above integral we get the desired result.
(Ill) Integration of Rational Fractions
An expression of the f(x)/g(x), where f(x) and g(x) are polynomials in x, is called a rational fraction.
i.e., 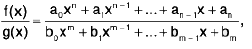
where a0, a1, an, b0, b1f ..., bm are constants and m, n ∈ N.
Type of fractions
(i) Proper fraction :
If degree of f(x) < degree of g(x), f(x)/g(x) is called a proper fraction.
Example 11: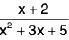 is a proper fraction.
is a proper fraction.
∵ Here degree of numerator = 1 and degree of denominator = 2
∴ degree of numerator < degree of denominator.
(ii) Improper fraction :
If degree of f(x) > degree of g(x), f(x)/g(x) is called an improper fraction.
then divide f(x) by g(x) so that 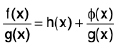
where h(x) is an integral function and 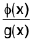 is a proper fraction.
is a proper fraction.
Example 12 : 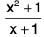 is an improper fraction.
is an improper fraction.
∵ Here degree of numerator = 2 and degree of denominator = 1
∴ degree of numerator > degree of denominator
Then divide (x2 + 1) by (x + 1) such that
∴
Here (x - 1) is an integral function and 2/x + 1 is a proper fraction .
Any proper fraction can be expressed as the sum of two or more simple fractions. Each such fraction is called a partial fraction and the process of obtaining them is called the resolution or decomposition of f(x)/g(x) into partial fractions.
Case I : Integration of fractions with non-repeated linear factors in the denominator.
An non-repeated linear factor (x - a ) of denominator then corresponds a partial fraction of the form 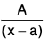 where A is constant to be determined
where A is constant to be determined
If g(x) = (x - a1) (x - a2) ... (x - an) then we assume that
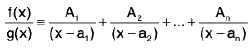
Example 13 : Evaluate : 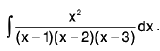
Let I =
Here
then x2 = A (x - 2) (x - 3) + B (x - 3) (x - 1) + C(x - 1) (x - 2) -----(1)
Putting x = 1, 2 and 3 successively on both sides of (1), we get A = 1/2, B = - 4 and C = 9/2.
=
=
=
Two Important deductions of case I
Deduction I : If everywhere same quantity in the given fraction then put same quantity equal to another quantity for the sake of partial fractions that at last substitute the value of another quantity.
Example 14 : Evaluate: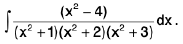
Let I =
The given fraction has everywhere x2. Put x2 = t for the sake of partial fractions
∴
=
----(1)
∴
=
=
and
Substituting the values of A, B and C in (1), we have
or
∴
=
=
Deduction II : If f(x)/g(x) is an improper fraction, then after division let remainder ∅(x) has lower degree of g(x).
Let g(x) = (x - a1)(x - a2) ... (x - an)
then by actual division 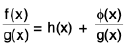
= 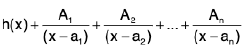
Example 15 : Evaluate : 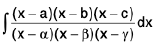
Let I =
The given fraction is an improper fraction then by actual division, since same degree in above and below.
i.e,
then
where f(x) is a polynomial of second degree
∴
----(1)
∴
=
and
=
Substituting the values of A, B and C in (1), we have

∴
=
=

Case II : Integration of fractions with repeated linear factors in the denominator
A repeated linear factor (x - a)n of denominator then corresponds partial fractions of the form
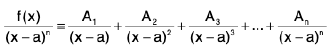
where A1, A2, A3, An are constants, can be determined equating the numerator of L.H .S. to the numerator of R.H.S. (after L.C.M.) and substituting x = a, we get A e.g., 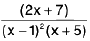 will be partial fractions of the form
will be partial fractions of the form 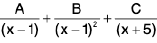 .
.
Example 16 : Evaluate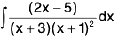
Let I =
here
---(1)
(2x - 5) = A(x + 1)2 + B(x + 1 )(x + 3) + C(x + 3) ---(2)
Putting x = - 1 and x = - 3 in (2), we get
Equating the coefficients of x2 on the sides of (2), we get 0 = A + B
B = 11/4
Substituting the values of A, B and C in (1), we have
∴
=
=
Case III: Integration of fractions with non repeated quadratic factors in the denominator
To every quadratic factor (which can not be factorized into linear factors) of the form ax2 + bx + c in the denominator, there will be partial fraction of the form Ax + B/ax2 + bx + c where A and B are constants to be determined.
e.g., 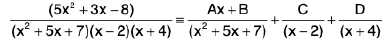
Example 17 : Evaluate :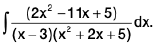
Let I =
Here
-----(1)
(2x2 - 11x + 5) = A(x2 + 2x + 5) + (Bx + C)(x - 3) -----(2)
Putting x - 3 = 0 or x = 3 in (2), we get
A = -1/2
Equating the coefficients of x2 and x in (2), we have
2 = A + B, - 11 = 2 A - 3B + C
then B = 5/2 and C = -5/2
Substituting the values of A, B and C in (1), we have

Example 18 : Evaluate : 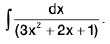
Let I =
=
=
=
=
(ii) 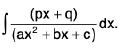
Rule : Here we express the numerator as follows :
Numerator = / (Differential coefficient of Denominator) + m where / and m are constants,
i.e., 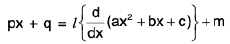
or px + q = /(2ax + b) + m
Comparing the coefficient of x and constant terms on both sides, we get
p = 2a/ and q = b/ + m
∴ 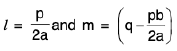
∴ 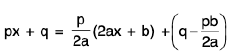
Thus, we get 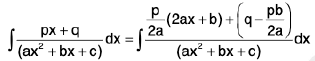
= 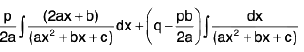
= 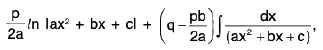
the integral on R.H.S. can be evaluated easily as in (i).
Example 19 : Evaluate : 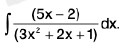
Let I =
----(1)
so we write 5x - 2 = / (6x + 2) + m
Comparing the coefficient of x and constant terms, we get
5 = 5/ and - 2 = 2/ + m
∴

∴
=
=
=
(iii) 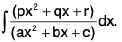
Rule : Here express the numerator as follows :
Numerator = / (Denominator) + m (Differential coefficient of Denominator) + n
where /, m, n are constants.
i.e., px2 + qx + r = / (ax2 + bx + c) + 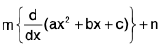
or px2 + qx + r = / (ax2 + bx + c) + m(2ax + b) + n
Comparing the coefficients of x2, x and constant terms on both sides, we have
p = /a, q = b/ + 2am and r = /c + mb + n
then we get
and 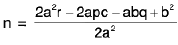 ---------(1)
---------(1)
Then, we get 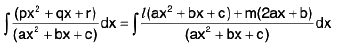
= 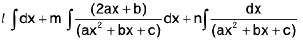
= 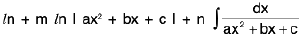
the integral on R.H.S. can be evaluated easily and in last substitute the values of /, m & n from (1).
Example 20 : Evaluate :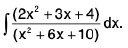
Let I =
W e write 2x2 + 3x + 4 = /(x2 + 6x + 10) +
= /(x2 + 6x + 10) + m(2x + 6) + n
Comparing the coefficients of x2, x and constant terms on both sides then we get
2 = /, 3 = 6/ + 2m and 4 = 10/ + 6m + n
∴ / = 2, m = - 9/2 and n = 11.
∴
=
=
=
=
(iv) 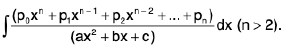
Rule : Here divide the numerator by denominator and express it as
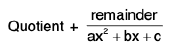
or 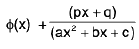
where ∅(x) will consist of certain terms which we shall integrate by power formula and 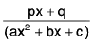 will be integrated as discussed in (ii)
will be integrated as discussed in (ii)
Example 20 : Evaluate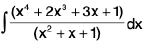
Let I =
Now,
∴
∴
=
=
=
=
Integrals of the form
(i) 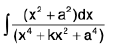
(ii) 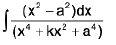
(iii) 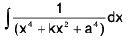
(iv) 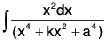 where k is any constant
where k is any constant
(i) 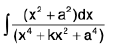
Rule : Divide above and below by x2 , then
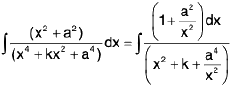
Here integral of the numerator = x = x - a2/x
= 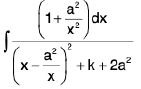
Put x - a2/x = t ∴ 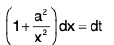
then 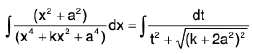
which is of the form 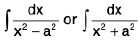 and can be integrated.
and can be integrated.
Example 21 : Evaluate : 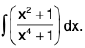
Let I =
Dividing the numerator and denominator by x2, we get
Put
so that
∴
=
Example 22 : Evaluate :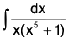
Let I =
=
Put 1 + x-5 = t
∴ - 5x-6 dx = dt or
then I =
=
(ii) 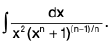
Rule : Taking xn common and put 1 + x-n = t
∴ 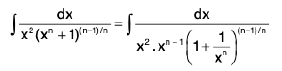
= 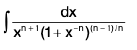
Put 1 + x-n = t
∴ 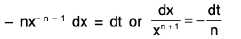
then 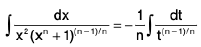
= 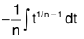
= 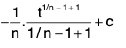
= 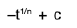
= 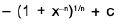
In 1st integral put x2 + 2x + 3 = t and in second integral put x + 1 = u
∴ (2x + 2)dx = dt and dx = du
then I = 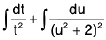
= 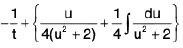
= 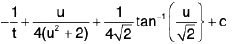
Hence I = 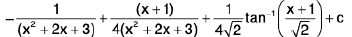
Integration of Irrational Functions
Integration by Rationalisation :
Rule : Multiplying the numerator and the denominator by the same quantity then the numerator or denominator transforms the irrational function into any of the standard results.
Example 23 : Evaluate :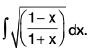
Let I =
=
Multiplying above and below by √(1 - x ) , we get
=
=
in second integral on R.H.S. put 1 - x2 = t2
∴ - x dx = t dt
then
=
=
=
Integrals of the form
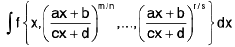
where f is the rational function of its arguments.
Rule : In this form substitute 
where a is L.C.M. of the denominator of the fractions m/n,...., r/s i.e. L.C.M of n,...,s.
Example 24 : Evaluate : 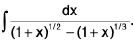
Let I =
Here L.C.M. of 2 and 3 is 6 put 1 + x = t6
∴ dx = 6t5 dt
then
=
=
Integrals of the form
(i) 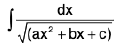
(ii) 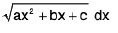
(iii) 
(iv) 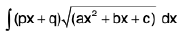
(v) 
(vi) 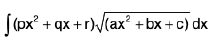
(i) 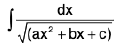
Rule : We have
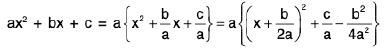
∴ 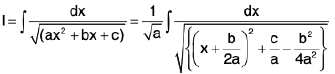
Case I : If b2 — 4ac > 0 and a > 0
then 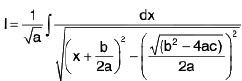
which is of the form 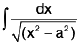 and can be integrated .
and can be integrated .
Case II : If a is negative . Let a = -λ .
∴ 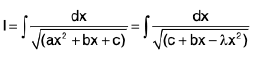
= 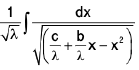
= 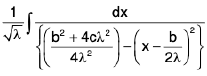
= 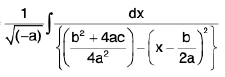

which is of the form 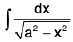 and can be integrated.
and can be integrated.
Example 25 : Evaluate :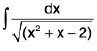
Let I =
=
We know
(v) 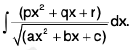
Rule : We can express the numerator as follows :
px2 + qx + r = l(ax2 + bx + c) + 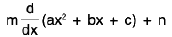
or px2 + qx + r = l(ax2 + bx + c) + m (2ax + b) + n
where /, m and n are constants
Comparing the coefficients of x2, x and constant terms on both sides, we get
p = al, q = bl + 2am and r = lc + bm + n
∴  -----(1)
-----(1)
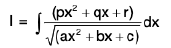
= 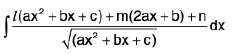
= 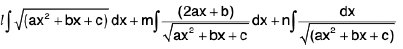
= 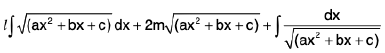 -----(2)
-----(2)
The integrals on R.H.S. can be evaluated easily as in (i) and (ii) and at last substituting the values of /, m and n from (1) in (2).
Example 26 : Evaluate : 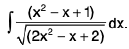
Let I =
Here x2 - x + 1 = /(2x2 - x + 2) +
or x2 - x + 1 = /(2x2 - x + 2) + m(4x - 1) + n
Comparing the coefficients of x2, x and constant terms on both sides, then
1 = 21, - 1 = - / + 4m and 1 = 2/ - m + n
∴ l = 1/2 and m = -1/8 and n = -1/8
(i) 
Rule : Here we put ax + b = t2
Note :
The above rule will be applicable if the numerator is the function of x and f(x) in places of unity
i.e., 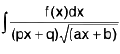 will be evaluated by the above rule.
will be evaluated by the above rule.
Example 27 : Evaluate : 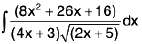
Let I =
Here 8x2 + 26x + 16 = (4x + 3)(2x + 5) + 1
then
=
In second integral on R.H.S. put 2x + 5 = t2
∴ 2dx = 2t dt or dx = t dt
∴
=
=
=
(ii) 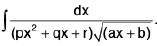
Rule : Here we put ax + b = t2
Note : The above rule will be applicable if the numerator is the function of x say f(x) in place of unity
i.e., 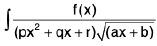 dx will be evaluated by the above rule.
dx will be evaluated by the above rule.
(iii) 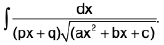
Rule : Here we put px + q = 1/t
Note : The above rule will be applicable if the numerator is the function of x say f(x) in place of unity.
i.e., 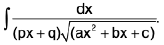 will be evaluated by the above rule.
will be evaluated by the above rule.
Examples 28 : Evaluate :
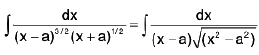
Let I =
Put x - a = 1/t
then
=
=
=
=

=
(iv) 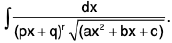
Rule : Here we put px + q = 1/t
Note : The above rule will be applicable if the numerator is the function of x say f(x) in place of unity
i.e., 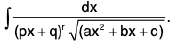 will be evaluated by the above rule.
will be evaluated by the above rule.
Example 29 : Evaluate : 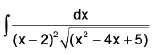
Let I =
Put x - 2 = 1/t
then
=
=
=
=
=
=
(v)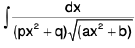
Let I = 
Put x =1/t
∴ 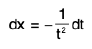
then 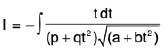
Now put a + bt2 = z2 ∴ 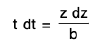
∴ 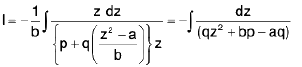
It can be easily evaluated from standard results.
Example 30 : Evaluate :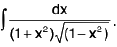
Let I =
Put x =1/t
∴
then
Again put t2 - 1 = z2 ∴ t dt = z dz
=
=
(∴ t2 - 1 = z2)
=

=
(vi) 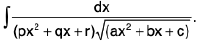
Rule : Here we put 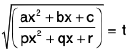
Example 31 : Evaluate : 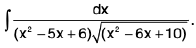
Let I =
∵
we get A = - 1 and B = 1
∴
then
=
In 1st integral put x - 3 = 1/t and in 2nd integral put x - 2 = 1/u on R.H.S.
Then, we get

=
=
=
=
=
=
Integration of Trigonometric Functions
Integration of the from ∫sinmx cosnx dx
Case I : If m is odd and n is even positive integer, then put cos x = t
Example 32 : Evaluate : ∫sin3xcos2x dx
Let I = ∫sin3xcos2x dx
Put cos x = t sin x dx = - dt
then I = ∫(1 — cos2 x)cos2 x sin x dx
= ∫ 1 - t2) t2 (-dt)
=
=
=
(∴cosx = t)
Case II : If m is even and n is odd positive integer, then put sin x = t.
Example 33 : Evaluate : ∫sin4xcos5x dx .
Let I = ∫sin4xcos5x dx
Put sin x = t ∴cos x dx = dt
then
=
=
=
=
Case III : If m and n both are odd positive integers,
then If m > n, put sin x = t
If m < n, put cos x = t
If m = n, put sin x = t or cos x = t
Example 34 : Evaluate : ∫sin5x cos3xd x .
Let I = ∫sin5x cos3xd x
Put sin x = t ∴cos x dx = dt
then
=
=
=
Case IV : If m + n = - ve and even integer then convert the given integrand in terms of tanx and sec2x then put tan x = t.
Example 35 : Evaluate :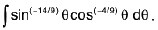
Let I =
Here m + n = -14/9 - 4/9 = -2 (-ve)
Since m + n = -ve, convert the given integrand in terms of tan x and sec2x
then
Put tanθ = t ⇒sec2θ dθ = dt
then
=
=
Case V : If m and n are small even integers, then convert them in terms of multiple angles by using the formulae
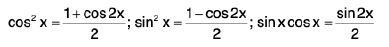
and 2 cos x cos y = cos(x + y) + cos (x - y)
Examples 36 : Evaluate : ∫sin4x cos2x dx
Let I = ∫sin4x cos2x dx
=
=
=
=
=
=
=
=
Case VI : If m and n are large even positive integers then change in multiple angles with the help of complex numbers.
if 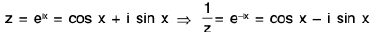
∴ 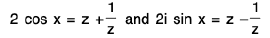
In general, If zn = cos nx + i sin nx then 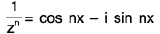
Since cos(-x) = cosx and sin(-x) = - sinx
Evaluate I = ∫sin6x cos4x dx ------(1)
From (1), 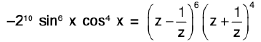 x
x
= 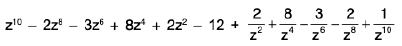
= 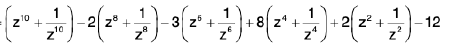
= 2 cos 10x - 2 . 2 cos 8x - 3 . 2 cos 6x + 8 . 2 cos 4x + 2 . 2 cos 2x - 12
= 2{cos 10x - 2 cos 8x - 3 cos 6x + 8 cos 4x + 2 cos2x - 6}
or 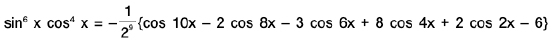
so I = ∫sin6x cos4x dx
= 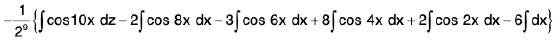
= 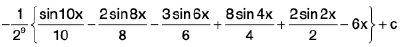
Hence I = 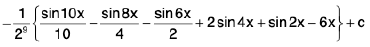
Integral of the form
∫tanmx secnx dx
Rule : (i) If m is even or odd integer and n is even positive integer than put tan x = t.
(ii) If m is odd positive integer and n even positive integer then put sec x = t. (
iii) If m = 0 and n = 2r + 1 ∀ r∈ N
then 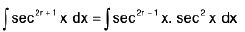
then integrate by parts taking sec2x as second function.
Note : If m e even positive integer and n ∈ odd positive integer, then integral is non-integrable.
Example 37 : Evaluate : ∫tan2x sec2xdx
By Using Ist rule
Here m = 2 and n = 2 So
let tanx = t ⇒ sec2x dx = dt
⇒We can also solve it by using integral by parts as taking tan2x is 1st function and sec2 x as IInd function.
Integral of the form
∫cotmxcosecnx dx
Rule :
(i) If m is even or odd integer and n is given positive integer then put cot x = t.
(ii) If m is odd positive integer and n ∈ even positive integer then put cosec x = t
(iii) If m = 0 and n = 2r + 1 ∀ r ∈ N
then 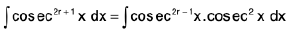
integrate by parts taking cosec2x as second function.
Note : If m ∈ even positive integer and n e odd positive integer then integral is non-integrable.
Example 38 : Evaluate : ∫cot2x cosec4x dx.
Let I = ∫cot2x cosec4x dx
Here m = 2 and n = 4
or
(since cosec2x = 1 + cot2x)
Put cot x = t
∴ - cosec2 x dx = dt
⇒ cosec2 x dx = - dt
then
=
=
=
|
98 videos|28 docs|30 tests
|
FAQs on Basic Integration- I - Mathematics for Competitive Exams
| 1. What is the concept of antiderivatives in the context of differentiation in reverse? |  |
| 2. How can we interpret integration geometrically? |  |
| 3. What are some properties of the indefinite integral? |  |
| 4. What are the different methods of integration? |  |
| 5. How do we integrate irrational functions? |  |
























 then we get
then we get [∴ z = tan-1 t]
[∴ z = tan-1 t]

















 (∵t = 1 - x2)
(∵t = 1 - x2)






 = 2
= 2 ......(1)
......(1)


























 ----(1)
----(1)













 ----(1)
----(1)











 ---(1)
---(1)





 -----(1)
-----(1)





 ----(1)
----(1)






















 so that
so that 























































 (∴ t2 - 1 = z2)
(∴ t2 - 1 = z2)



 we get A = - 1 and B = 1
we get A = - 1 and B = 1












 (∴cosx = t)
(∴cosx = t)























 (since cosec2x = 1 + cot2x)
(since cosec2x = 1 + cot2x)























