Basic Integration- II | Mathematics for Competitive Exams PDF Download
Integrals of the form
(i) 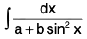
(ii) 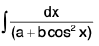
(iii) 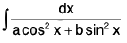
(iv) 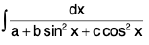
(v) 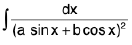
(vi) 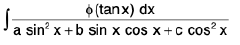
where a, b, c ∈ R and not at a time all zero.
Rule : We shall always in such cases divide above and below by cos2 x; then put tan x = t i.e., sec2 x dx = dt then the questions shall reduce to the forms 
Example 39 : Evaluate :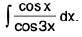
Let I =
=
=
Divide above and below by cos2x, then
=
Put √3 tan x = t
=
=
=
=
Integrals of the form
(i) 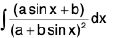
(ii) 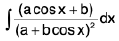
(iii) 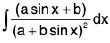
Rule : Divide above and below by cos2 x, then
Put a sec x + b tan x = t
Example 40 : Evaluate : 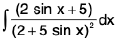
Let I =
Divide above and below by cos2 x, then

Put 2 sec x + 5 tan x = t
∴ (2 sec x tan x + 5 sec2 x) dx = dt
∴
=
=
(ii) 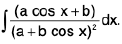
Rule : Divide above and below by sin2 x, then
Put a cosec x + b cot x = t
Example 41: Evaluate :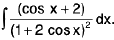
Let I =
Divide above and below by sin2 x, then
Put cosec x + 2 cot x = t
∴ (- cosec x cot x - 2 cosec2 x) dx = dt
or (cosec x cot x + 2 cosec2 x) dx = - dt
then
=
=
Integrals of the form
(i) 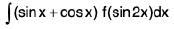
(ii) 
(i) 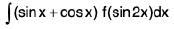
Rule : Since integral for sin x + cos x is sin x - cos x
Put sinx - cos x = t ∴(cos x + sin x) dx = dt
and sin2 x + cos2 x - 2 sin x cos x = t2 or sin 2x = 1 - t2
then 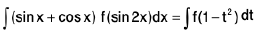 it can be evaluated easily.
it can be evaluated easily.
Example 42 : Evaluate : 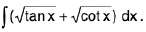
Let I =
=
=
Put sin x - cos x = t ∴(cos x + sin x) dx = dt
and sin2 x + cos2 x - 2 sin x cos x = t2
⇒
then
=
=
(ii) 
Rule : Since integral of sin x - cos x is - cos x - sin x
Put sin x + cos x = t (cos x - sin x) dx = dt
and sin2 x + cos2 x + 2 sin x cos x = t2
or sin 2x = t2 - 1
then 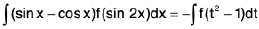 it can be evaluated easily.
it can be evaluated easily.
Example 43 : Evaluate : 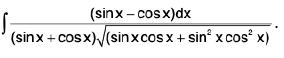
Let I =
Put sin x + cos x = t (cos x - sin x) dx = dt
⇒ (sin x - cos x) dx = - dt
and sin2 x + cos2 x + 2 sin x cos x = t2
⇒
then
=
=
Again put t4 - 1 = z2
⇒ 4t3 dt = 2z dz or 2t3 dt = z dz
then
=
=
Integral of the form
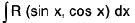
Rule :
(i) If R ( - sin x, cos x) = - R (sin x, cos x) then put cos x = t
(ii) If R (sin x, - cos x) = - R (sin x, cos x) then put sin x = t
(iii) If R ( - sin x, - cos x) = R (sin x, cos x) then put tan x = t
Example 44 : Evaluate :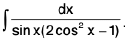
Let I =
Let
⇒
therefore we put cos x = t ∴ sin x dx = - dt
∵
=
=
=
=
=
=
=
Integrals of the form
(i) 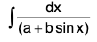
(ii) 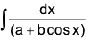
(iii) 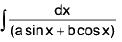
(iv) 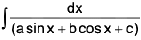
(v)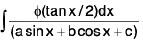
(vi) 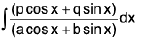
(vii) 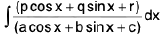
Rule for (i), (ii), (iii), (iv), (v) :
Write cos x = 
the numerator will become sec2(x/2) and the denominator will be a quadratic in tan(x/2). Putting tan(x/2) = t i.e., sec2(x/2) dx = 2 dt the question will reduces to the form
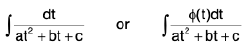
Example 45 : Evaluate :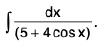
Let I =
=
=
Put tan (x/2) = t ∴ sec2 (x/2) dx = 2 dt
then I =
=
Integrals of the form
(i) 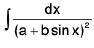
(ii) 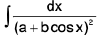
(i) 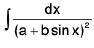
Rule : Put t = 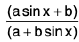 -----(1)
-----(1)
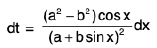 or
or 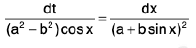 -----(2)
-----(2)
Example 46 : Evaluate 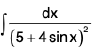
Put
-----(1)
∴
-----(2)
From (1), sin x =
then cos x =
From (2),
Integrating both sides, we get
Let 1 - t2 = z2⇒ - tdt = zdz
=
=
=
=
=

(ii) 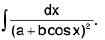
Rule : Put t = 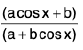 ------(1)
------(1)
∴ 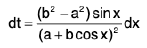 or
or 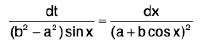
Now substitute the value of sin x in L.H.S. from (1) in terms of t and then integrate both sides.
Example 47 : Evaluate : 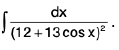
Let I =

Put
------(1)
∴
or
------(2)
From (1),
∴
From (2),
Integrating both sides, we get
=
=
Integrals of the form
(i) 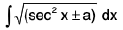
(ii) 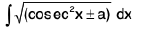
(iii) 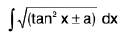
(iv)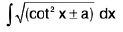
(i) 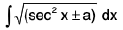
Rule :
Let I = 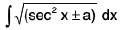 =
= 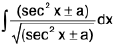
= 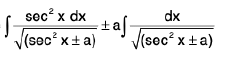
= 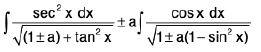
In first integral on R.H.S. put tan x = t and in second integral put sin x = u
Example 48 : Evaluate : 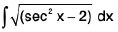
Let I =
=
=
=
=
In first integral on R.H.S. put tan x = t and in second integral put √sin x = u.
i.e., sec2 x dx = dt and cos x dx = du/√2
=
=
(iii) 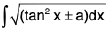 and
and
(iv) 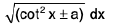
Rule : In this case change tan2 x into sec2 x - 1 and cot2 x into cosec2 x - 1 and then proceed as in (i) and (ii).
Integrals of the form
(i) 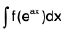
(ii) 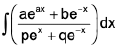
(i) 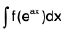
Rule : Transform into an integral of a rational function by the substitution eax = t.
Example 49 : Evaluate : 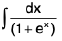
Let I =

Divide above and below by ex then
Put 1 + ex = t ∴ ex dx = - dt
then
= = - In t + c
= - In (1 + e-x) + c
(ii) 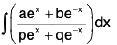
Rule : Express numerator as / (Denominator) + md/dx(Denominator)
Find l and m by comparing the coefficients of ex and e-x and split the integral into sum of two integrals as
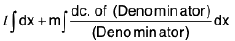
= /x + m /n I Denominator I + c
Example 50 : Evaluate : 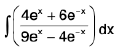
Let I =
Express Numerator as
⇒ Numerator =/ (Denominator) + md/dx(Denominator)
or (4ex + 6e-x) = /(9ex - 4e-x) + m(9ex + 4e-x)
Comparing the coefficients of ex and e-x on both sides then
4 = 9/ + 9m and 6 = - 4 / + 4m
After solving we get
then I =
=
=
The Integral of A Binomial Differential
A binomial differential is a differential of the form xm (a + bxn)p dx where m, n, p ∈ Q and a, b are constants not equal to zero. The integral
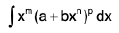
is expressible in terms of elementary functions in the following three cases :
Case 1 : (i) If p ∈ N then expand by the formula of Newton Binomial.
(ii) If p < 0, then we put x = tk where k is the common denominator of the fractions m and n.
Case 2 : If 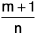 = Integer then we put a + bxn = tα where α is the denominator of the fraction p.
= Integer then we put a + bxn = tα where α is the denominator of the fraction p.
Example 51 : Evaluate :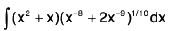
Let I =
=
=
Put x2 + 2x = t
∴
∴
=
DEFINITE INTEGRALS AND THEIR PROPERTIES
Definition : Let f be a function which is continuous on the closed interval [a, b]. The definite integral of f(x) from a to b is defined to be the limit
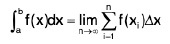
where 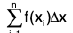
is a Riemann sum of f(x) on [a, b]
Newton-Leibnitz Formula
Let f be a function of x defined in the closed interval [a, b] and the function F is an antiderivative of f on [a, b], such that F’(x) = f(x) for all x in the domain of f, then
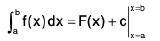
= (F(b) + c) - (F(a) + c)
= F(b) - F(b)
Note : In definite integrals, constant of integration is never present.
Rule for Finding Definite Integral
To evaluate the definite integral 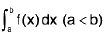
First find out the indefinite integral of f(x) i.e., ∫f(x)dx, leaving the constant of integration c.
Let 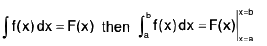
= 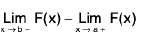
To evaluate above the following cases may arise :
Case I : If f(x) is continuous at x = a and x = b :
∴ 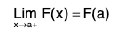 and
and 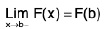
then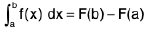
Case II : If f(x) is continuous at x = a and discontinuous at x = b :
∴ 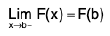
then 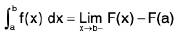
Case III : If f(x) is discontinuous at x = a and continuous at x = b :
∴ 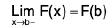
Case III : If f(x) is discontinuous at x = a and continuous at x = b :
∴ 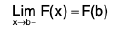
then 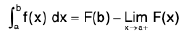
Case IV : If f(x) is discontinuous at x = c (a < c < b) :
f(x) is discontinuous at x = c or f(x) has different values in (a, c) and (c, b) then
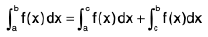
Note : If f(x) is not defined at x = a and x = b and defined in open interval (a, b) then 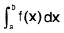 can be evaluated.
can be evaluated.
Example 51 : Evaluate :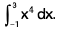
= 244/5
Geometrical Interpretation of the Definite Integral
First we construct the graph of the integrand y = f(x) then in the case of f(x) > 0 ∀ x ∈ [a, b], the integral J f(x) dx is numerically equal to the area bounded by the curve y = f(x), the x-axis and the ordinates x = a and x = b.

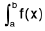 dx is numerically equal to the area of curvilinear trapezoid bounded by the given curve, the straight lines x = a and x = b, and the x-axis.
dx is numerically equal to the area of curvilinear trapezoid bounded by the given curve, the straight lines x = a and x = b, and the x-axis.
In general : 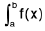 dx represents an algebraic sum of areas of the region bounded by the curve y = f(x), the x-axis and the ordinates x = a and
dx represents an algebraic sum of areas of the region bounded by the curve y = f(x), the x-axis and the ordinates x = a and
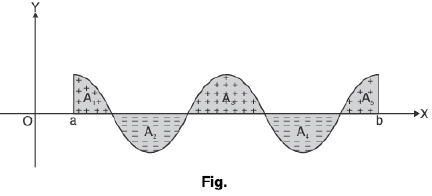
x = b. The areas above the x-axis enter into this sum with a positive sign, while those below the x-axis enter it with a negative sign.
∴ 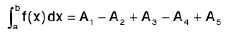
where A1, A2, A3, A4, A5 are the areas of the shaded regions.
Example 52 : Evaluate : 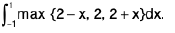
To find
when x < 0
y = max{2 - x, 2, 1 + x} = 2 - x
when x > 0
y = max{2 - x, 2, 1 + x) = 2
Plotting these curves on the XY plane
= Area of shaded region
= Area of square ABCD + Area of ADEF
= 2 x 2 + 1/2 x 1 x 1
= 4 + 1/2
= 9/2
Example 53 : Evaluate :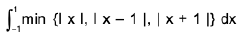
The graph of f(x) = min {I x I, I x - 1 |, | x + 1 |} is shown as in Fig..
Therefore
= Area of shaded region
=
Example 54 : Evaluate : 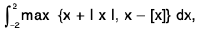 where [x] denotes the greatest integer ≤ x.
where [x] denotes the greatest integer ≤ x.
I =
=
=
= 1 + 1 + 3
= 5
Definite Integral by standard methods of indefinite integral
(i) Transformation Method : To evaluate the integral 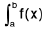 dx we can transform f(x) into other function ∅(x) without any substitution then
dx we can transform f(x) into other function ∅(x) without any substitution then
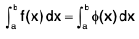
and then 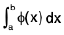 evaluate easily.
evaluate easily.
Example 56 : Evaluate :
Let I =
=
=
=
=
=
(ii) Substitution Method : By the substitution x = ∅(x) in the definite integral ∫ f(x)dx, the lower and the upper limits change.
When x = a then a = ∅(t) ⇒ t = ∅-1(a)
and when x = b then b = ∅(t) ⇒ t = ∅-1 (b)
Hence the new lower and upper limits are ∅-1(a) and ∅-1(b) respectively.
Again put In 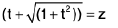
∴ 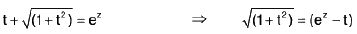
⇒ 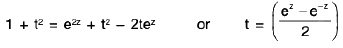
∴ 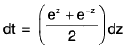
When t = 0 ⇒ z = 0
t = ∝ ⇒ z = ∝

= 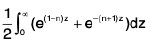
= 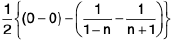
= 
= 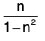
(iii) By Parts Method : Let u and v are the functions of x, u and v have continuous derivatives on the interval [a, b]. Then
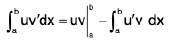
where u' and v’ are the derivatives of u and v respectively.
Example 57 : Evaluate :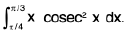
Integration by parts, Definite Integral
=
=
=
=
=
=
=
=
=
Properties of The Definite Integral
Some simple properties of definite integrals can be derived from the basic definition, or from the Fundamental Theorem of the Calculus.
(a) 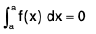
If the upper and lower limits of the integral are the same, the integral is zero. This becomes obvious if we have a positive function and can interpret the integral in terms of ‘the area under a curve’.
(b) If a ≤ b ≤ c,
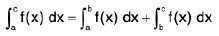
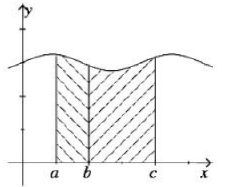
This says that the integral of a function over the union of two intervals is equal to the sum of the integrals over each of the intervals. The diagram opposite helps to make this clear if f(x) is a positive function.
(c) 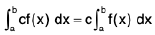 for any constant c.
for any constant c.
This tells us that we can move a constant past the integral sign but we can only do this with constants, never with variables!
(d) 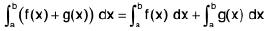
That is, the integral of sum is equal to the sum of the integrals.
(e) If f(x) ≤ g(x) in [a, b] then
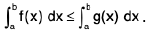
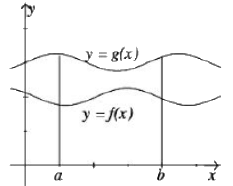
That is, integration preserves inequalities between functions. The diagram opposite explains this result if f(x) and g(x) are positive functions.
(f) 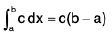
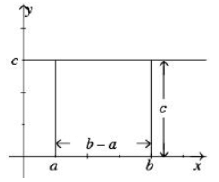
This tells us that the integral of a constant is equal to the product of the constant and the range of integration. It becomes obvious when we look at the diagram with c > 0, since the area represented by the integral is just a rectangle of height c and width b - a.
(g) We can combine (e) and (f) to give the result that, if M is any upper bound and m any lower bound for f(x) in the interval [a, b], so that m ≤ f(x) ≤ M, then
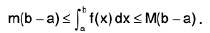
This, too becomes clear when f(x) is a positive function and we can interpret the integral as the area under the curve.
(h) Finally we extend the definition of the definite integral slightly, to remove the restriction that the lower limit of the integral must be a smaller number than the upper limit. We do this by specifying that
For example,
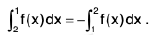
Example 58 : Evaluate :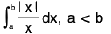
Let I =
Case I : When 0 < a < b
then
= I b I - | a | -------------(1)
Case II : When a < 0 < b
then I =
= - (0 - a) + (b - 0)
= b + a ...(2)
= I b I - | a | -------------(2)
Case III : When a < b < 0
then
= I b I - | a | -------------(3)
It is clear from (1), (2) and (3) we get
Example 59 : Evaluate : 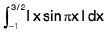
Let I =
=

=
=
=
Some other properties
Property :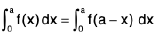
Proof : Analytical Method :
R.H.S. = 
Put a - x = t ∴dx = - dt
When x = 0 ⇒ t = a
x = a ⇒ t = 0
∴ R.H.S. = 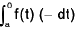
= 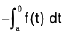
= 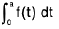
= 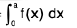
= L.H.S.
Removal of x : Let I = 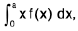 where f(x) is a function of x whose integral is known and f(a - x) = f(x) then apply above property.
where f(x) is a function of x whose integral is known and f(a - x) = f(x) then apply above property.
Example 60 : Evaluate : 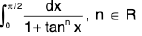
Let I =
...(1)
=
=
...(2)
Adding (1) and (2),
Hence I = π/4
Hence remember that :
(i) 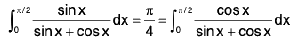
(ii) 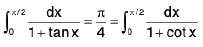
(iii) 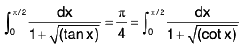
(iv) 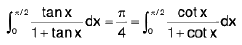
(v) 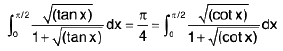
(vi) 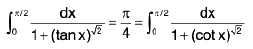
Example 61 : Evaluate : 
Let I =
put t = 1 - x ⇒ dt = - dx
at x = 0 ⇒ t = 1
and x = 1 ⇒ t = 0
=
=
=
=
=
Example 62 : Evaluate : 
Let I =
...(1)
=
=
...(2)
Adding ( 1 ) and (2), we get
Put cos = t ∴ sin x dx = - dt
When x = 0 ⇒ t = 1
x = π ⇒ t = -1
∴
=
=
Hence I = π2/4
Remember that :
(i) 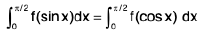
(ii) 
(iii) 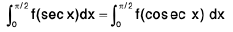
Property :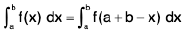
Note : In 95% cases a + b = π/4, π/2, π and in 5% cases a + b = 1, 2, 3, λ etc.
Example 63 : Evaluate : 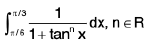
Let I =
=
----(1)
=
=
---(2)
adding (1) and (2), we get
= π/6
Hence I = π/12
Property :
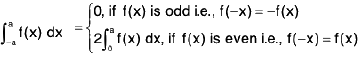
Example 64 : Evaluate : 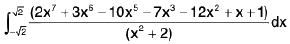
Let I =
=
=

=
=
=
=
=
=
Property :
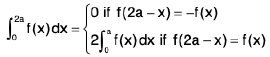
Example 65 : Evaluate : 
Let I =
----(1)
=
=
----(2)
Adding (1) and (2),
=
=
=
Put 2x = t ⇒ dx = dt/2
When x = 0 ⇒ t = 0
x = π/2 ⇒ t = π
∴
Here if f(t) = In sin t
f(π - t) = In sin (π - t) = In sin t = f(t)
then
=
∴
Hence remember that :
(i) 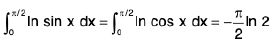
(ii) 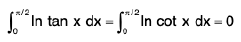
(iii) 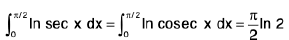
Example 66: Show that 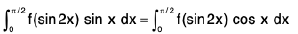 =
= 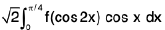
Let I =
----(1)
=
=
=
Adding (1) and (2), we get
=
=
Put x = π/4 - t => dx = - dt
When x = 0 ⇒ t = π/4
x = π/2 ⇒ t = -π/4
∴
=
=
=
Hence I =
Property : (Time Saving Property or Help line property)
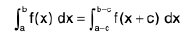
and 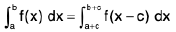
Analytical Method :
Put x + c = t dx = dt
W hen x = a - c ⇒ t = a
x = b - c ⇒ t = b
then 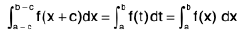
Also put x - c = t
∴ dx = dt
When x = a + c ⇒ t = a
x = b + c ⇒ t = b
then 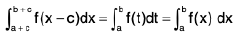
Example 67 : Show that the sum of two integrals 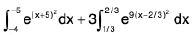 is zero.
is zero.
Let I =
=
=
Put 3x = - t in second integral then
3 dx = - dt
When x = - 1/3 ⇒ t = 1
x = 0 ⇒ t = 0
then
=
=
Example 68 : If f(x) = 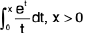 then prove that
then prove that 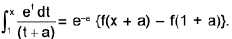
R.H.S. =
=
=
=
=
=
put at at
t - a = u ⇒ dt = du
t = 1 + a we get u = 1
t = x + a we get u = x
=
=
= L.H.S.
Property : (Time Saving property or Help line property)
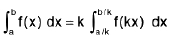
and 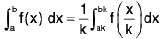
Example 69 : Evaluate : 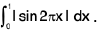
Let 2πx = t ⇒ 2π dx = dt ⇒ dx = dt/2
if x = 0 ⇒ t = 0 ; x = 1 ⇒ t = 2π
⇒
=
=
=
=
Example 70 : Show that 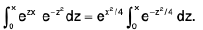
Let I =
(here x is constant)
put
∴
when z = 0 ⇒ t = - x
z = x ⇒ t = x
∴
=
=
=
(∴ Function is even)
=
OR
=
=
=
=
put z - x/2 = t ⇒ dz = dt
at z = 0 we get t = -x/2
at z = x we get t = x/2
=
put t = u/2 ⇒ dt = du/2
at t = -x/2 we get u = -x
at t = x/2 we get u = x
=
=
(∴ Function is even)
=
= R.H.S.
Property : (Reflection Property)
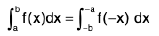
Proof. Analytical Method :
Let I = 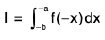 ----(1)
----(1)
Put - x = t ∴dx = - dt
when x = - b ⇒ t = b
x = - a ⇒ t = a
then 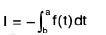
= 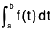
= 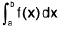 ----(2)
----(2)
From (1) and (2), we get
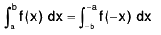
Graphical Method
The curve y = f(-x) is obtained with the help of y = f(x), v y = f(-x) is the mirror image of y = f(x) in the y-axis. It is clear from the Fig..

Area of ABCDA = Area of BA’C’D’A
then 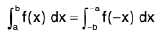
Example 71 : Evaluate : 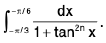
Let I =
=
=
----(1)
and
=
----(2)
Adding (1) & (2) we get
∴ I = π/12
Property : If f(x) is discontinuous at x = a then
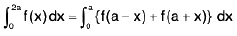
Proof : R.H .S . = 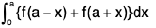
= 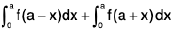
= 
= 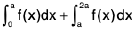
= 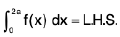
Example 72 : Evaluate : 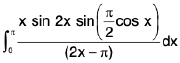
Let I =
Integrand is discontinuous at x = π/2 then

=
=
=
=
Put
then cos x dx =
∴
=
=
=
Property :
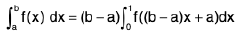
Example 73 : Given 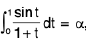 , find the value of
, find the value of 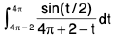 in terms of α.
in terms of α.
Let I =
Where a = 4π - 2 , b = 4π, f( t) =
according to property
I =
=

=
(substitute t = 1- t)
=
=

=
= - α (given)
Property :

where T is the period of the function and n ∈ I
i.e., f(x + T) = f(x)
Example 74 : Evaluate : 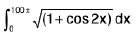
Let I =

=
=
=
( ∴ I cos x I is periodic with period π )
=
=

=
=
= 200√2
Property : 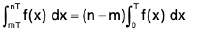
where T is the period of the function and m, n ∈ I
i.e., f(x + T) = f(x)
Proof. L.H.S. = 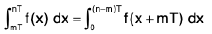
= 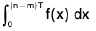 (∴ f(x) is periodic)
(∴ f(x) is periodic)
= 
= R.H.S.
Example 75 : Evaluate : 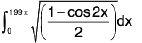
Let I =
=
=
( ∴I sin x I is periodic with period π )
=
=
= 200 (1 - (-1)) = 400
Property :
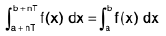
where T is the period of the function and n ∈ I
i.e., f(x + T) = f(x)
Proof. L.H.S. = 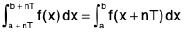
= 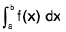 ( ∴ f(x + nT) = f(x))
( ∴ f(x + nT) = f(x))
= R.H.S.
Example 76 : Show that 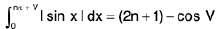 where n ∈ N and 0 ≤ V ≤ π.
where n ∈ N and 0 ≤ V ≤ π.
Let I =
=
=
(∴ I sin x I is periodic with period π)
=
( ∴ 0 ≤ V ≤ n )
=
= n(1 - ( - 1 ) ) + ( - cos V + 1)
= (2n + 1) - cos V
Example 77 : Find the value of 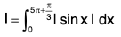
I =
=
=
=
Property : Leibnitz’s Rule :
(i) If u(x) and v(x) are differentiable functions of x whose values lie in [a, b] and f(x, t) is continuous then
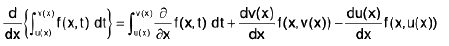
Note : Where d/dx f(x, t)
represents the differentiation with respect to x treating t as constant.
(ii) If f is continuous function on [a, b] and u(x) and v(x) are differentiable functions of x whose values lie in [a, b] then
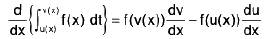
Example 78 : If 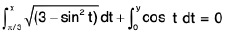 then evaluate dy/dx.
then evaluate dy/dx.
We have
Differentiating both sides w.r.t. x then
⇒
⇒
∴
Property :
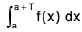 s independent of a
s independent of a
where T is the period of the function
i.e., f(x + T) = f(x)
Proof. Let I = 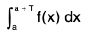
= 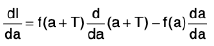
= f(a + T) . 1 - f(a) . 1
= f(a + T) - f(a)
= 0 { ∴ f(a + T) = f(a )}
Thus, I = c (independent of a)
Hence 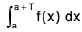 s independent of a
s independent of a
Example 79 : Evaluate : 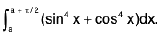
∴ sin4 x + cos4 x is periodic with period π/2 then
=
=
=
=
=
=
=
=
Property : Suppose that f(x, a) and fα’(x, a) are continuous functions when c ≤ α ≤ d and a ≤ x ≤ b then
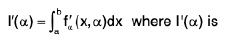
the derivative of 1(α) w.r.t. α and fα’(x, α) is the derivative of f(x, α) treating x as constant.
Example 80: Evaluate : 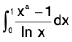
Let l(a) =

Where
then
According to property -
where I‘(a) is the derivative of l(a)
∴
=
Integrating both sides w.r.t. a then
l(a) = In (a + 1) + c
for a = 0, l(0) = In 1 + c
0 = 0 + c ⇒ c = 0
by equation (1)
∵ I(a) = ln(a + 1)
Property :
If f(t) is an odd function then ∅(x) = 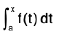 is an even function.
is an even function.
Proof. Since ∅(x) = 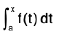
∴ 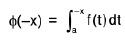
= 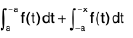
=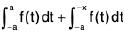
= 
= 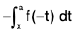
= 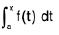
= ∅(x)
Hence ∅(-x) = ∅(x)
Example 81: Prove that F(x) = 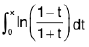 is an even function.
is an even function.
Let
∴
=
= -f(t)
⇒ f(-t) = -f(t) ∴ f(t) is an odd function.
Hence F(x) =
is an even function
Property :
If f(t) is an even function then ∅(x) = 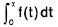 s an odd function.
s an odd function.
Proof. The proof is similar as above. Follow the same steps considering f(t) to be an even function.
Example 82 : Prove that F(x) = 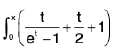 dt is an odd function.
dt is an odd function.
Let
∴
=
=
=
=
=
= f(t)
⇒ f(-t) = f(t) ∴f(t) is an even function.
Hence
is an odd function.
Important Note : If f(t) an even function then
is not necessarily an odd function for a ≠ 0. It will be an odd function if
Proof. Suppose

⇒
⇒
⇒
⇒
⇒
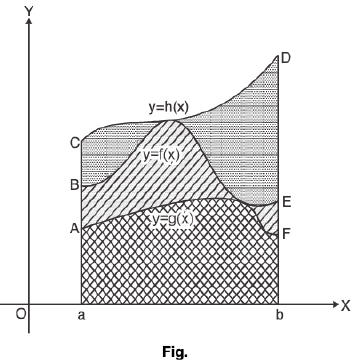
Property : If on an interval [a, b] (a < b), and the functions f(x) and g(x) satisfy the condition f(x) ≥ g(x) then
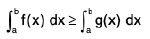
In Particular :
If f(x) ≥ 0 then 
Proof : Graphical Method :
As we know that 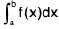 denotes the area under f(x) from a to b and if f(x) ≥ g(x) ∀ x ∈ (a, b) then clearly area under f(x) from a to b which can be seen by given fig.
denotes the area under f(x) from a to b and if f(x) ≥ g(x) ∀ x ∈ (a, b) then clearly area under f(x) from a to b which can be seen by given fig.
It is clear from the Fig. Area of curvilinear trapezoid aBCb ≥ Area of curvilinear trapezoid aADb then  and if
and if 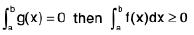

Example 83 : Prove that : 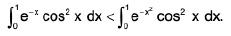
∴ 0 < x < 1
then x > x2 => - x < - x2
ex < ex2
then
Property : If at every point x of an interval [a, b] the inequalities 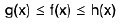 are fulfilled then
are fulfilled then 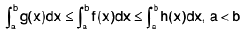
Proof. Graphical Method :
It is clear from the Fig.
Area of curvilinear trapezoid aAFb
≤ Area of curvilinear trapezoid aBEb
≤ Area of curvilinear trapezoid aCDb
i.e., 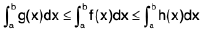
Example 84: Prove that : 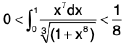
Since
then
Hence
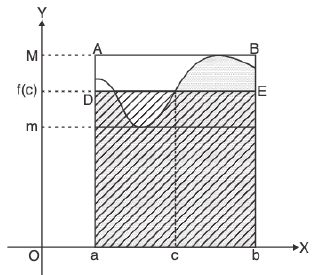
Property : If m is the least value (global minimum) and M is the greatest value (global maximum) of the function f(x) on the interval [a, b] (estimation of an integral). Then
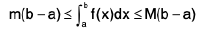
Proof : Analytical Method :
It is given that m ≤ f(x) ≤ M
then 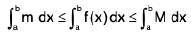
⇒ 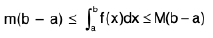
Graphical Method : It is clear from the Fig..
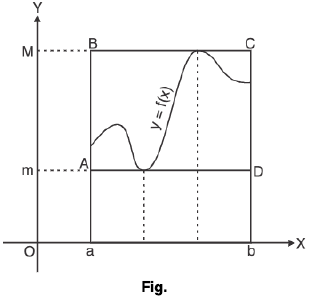
Area of abDA ≤ 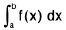 ≤ Area of aBCb
≤ Area of aBCb
i.e., 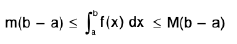
Example 85: Prove that 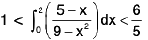
Let
∴
for critical points f’(x) = 0
∴ x = 9 and x = 1
∵ x ∈ [0, 2]) so we take x = 1.
then
f(0) = 5/9
f(1) = 1/2
f(2) = 3/5
∴ The greatest and the least values of the integral in the interval [0, 2] are respectively, equal to f(2) = 3/5 and f(1) = 1/2. Hence
or
Property : The following inequality is valid :
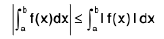 (a ≤ b)
(a ≤ b)
or if a is not necessarily less than b, then
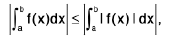
if f and I f I are integrable on [a, b].
Proof. Obviously, 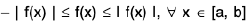
⇒ 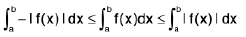 (a < b)
(a < b)
or 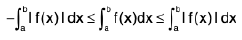
or 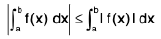
If 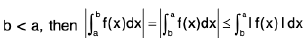
= 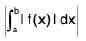
Hence 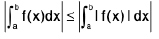
Example 86 : Estimate the absolute value of the integral 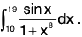
Since I sin x I ≤ 1 for x ≥ 10 then
---(1)≈
but 10 ≤ x ≤ 19
1 + x8 ≥ x8 ≥ 108
⇒
or
from (1) & (2) we get
∴
= (19 - 10) x 10-8
= 9x 10-8
= (10 - 1) x 10-8
= 10-7 - 10-8 < 10-7
Hence
∴ The true value of the integral ≈ 10-8
Property :
If f2(x) and g2(x) are integrable on the interval [a, b], the Schwarz-Bunyakovsky inequality takes place :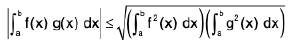
Proof. Let F(x) = (f(x) - λg(x)}2 > 0
∴ 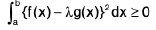
⇒ 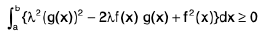
⇒ 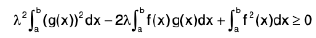
∴ Discriminant is one positive i.e., B2 - 4AC ≤ 0
⇒ 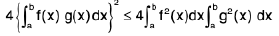
Hence 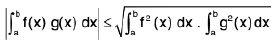
Example 87: Prove that 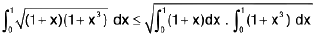
=
=
=
Hence
Property : If f(x) is continuous on [a, b] then there exists a point c ∈ (a, b) such that
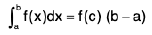
Then number 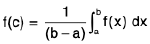 is called the Mean value of the function f(x) on the interval [a, b].
is called the Mean value of the function f(x) on the interval [a, b].
Proof : Analytical Method :
For a < b. If m & M are smallest and greatest values of f(x) on [a, b]
then 
or 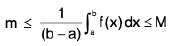
Since f(x) is continuous on [a, b], It takes on all intermediate values between m and M. Therefore, some values f(c) (a ≤ f(c) ≤ b), we will have
or 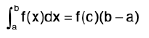
Graphical Method :
It is clear from the Fig.
Area of aABb = Area of aDEb
i.e., 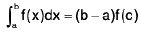 or
or 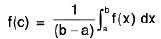
Note : Used of this property also in physics if we evaluate average of physical quantities.
i.e., Average speed = 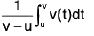
Example 88: Find the mean value of x(a - x) over the range (0, a).
Mean value =
=
=
=
The Root Mean Square Value (RMSV) of a function y = f(x) the range (a, b) is
Example 89: Find RMSV of In x over the range x = 1 to x = e
Here y = In x
...(1)
Now
=
=
=
∴
= (e - 2e + 2e) - (0 - 0 + 2)
= e - 2
From (1), we get
Property :
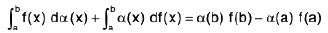
Example 90: Evaluate : 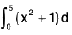 where [.] denotes the greatest integral function
where [.] denotes the greatest integral function
Here f(x) = x2 + 1 and a(x) = [x]
df(x) = 2xdx
According to property,
∴
⇒
=
=
= 130 - 70 = 60
Property :
(i) If the function f(x) increases and has a concave graph in the interval [a, b], then 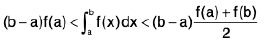
(ii) If the function f(x) increases and has a convex graph in the interval [a, b] then 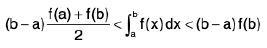
Example 91: Prove that : 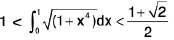
Let f(x) =
∴
∴ graph is concave up.
∴
⇒
Property : Improper Integrals :
(i) 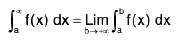
(ii) 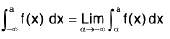
(iii) 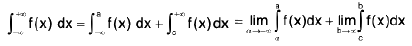
Example 92: Prove that 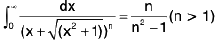
Put In
or
⇒
or
∴
∴
when x → 0, t → 0 and x → ∞, t → ∞
L.H.S. =
=
=
=
=
=
Definite Integral as the limit of a sum (Integration by First Principle Rule)
Let f(x) be a single valued continuous function in the interval (a, b), (a < b) and if the interval (a, b) be divided into n equal parts, each of width h, we have b - a = nh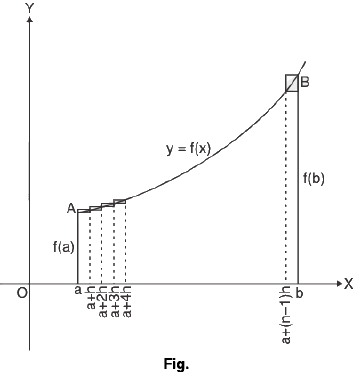
when n → ∞ then h→ 0
∴ 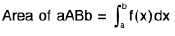
= 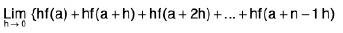
= 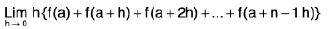
= 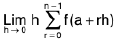
Hence 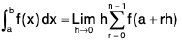
Some Important Results to Remember
(i) 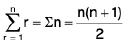
(ii) 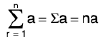
(iii) 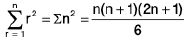
(iv) 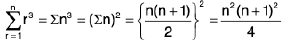
(v) 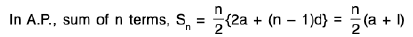
(vi) In G.P., sum of n terms , Sn = 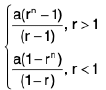
(vii) 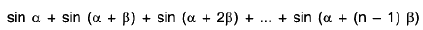 =
= 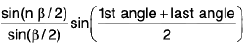
(viii) 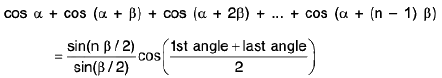
(ix) 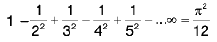
(x) 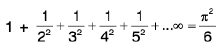
(xi) 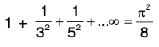
(xii) 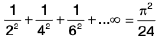
(xiii) 
(xiv) 
Example 93: Prove that 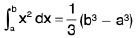 by first principle rule.
by first principle rule.
Here f(x) = x2, nh = b - a from the definition,
=
=
=
=
=
=
=
Example 94: From the definition of a definite integral as the limit of sum evaluate 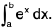
Here f(x) = ex, nh = b - a from the definition
=
=
=
=
=
=
= eb - ea
Summation of series by Integration
Let f(x) be a continuous function defined on the closed interval [a, b], then
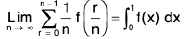
Rule : Here we proceed as follows :
(i) Express the given series in the form 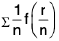
(ii) Then the limit is its sum when n → ∞
= 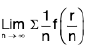
Replace r/n by x, 1/n by dx and 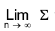 sign of ∫.
sign of ∫.
(iii) The lower and upper limits of integration will be the values of r/n for the first and last term (or the limit of these values) respectively.
when 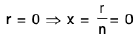
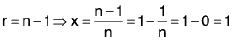
Note : 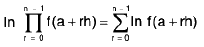
Example 95: Find the limit, when n → ∞ of 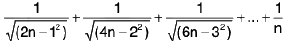
Let P =
=
=
=
let r/n = x
at r = 1 and as n → ∞, we get x → 0
at r = n and as n → ∞, we get x →1
Put x = t2 ∴ dx = 2t dt
when x = 0 ⇒ t = 0
x = 1 ⇒ t = 1
∴
=
Hence P = π/2.
Example 96: Find the limit, when n → ∞ of 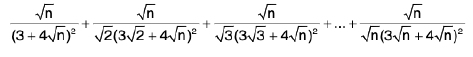
Let P =
P =
=
=
=
Put 3√x + 4 = t
∴
when x = 0 ⇒ t = 4
x = 1 ⇒ t = 7
∴
=
=
Hence P = 1/14
Gamma Function
The definite integral 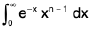 is called the Second Eulerian integral and is denoted by the symbol Гn (read as Gamma n).
is called the Second Eulerian integral and is denoted by the symbol Гn (read as Gamma n).
∴ 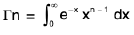
⇒ 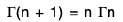
This formula is known as recurrence formula for Gamma function.
Important Formula :
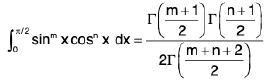
where m > -1 and n > -1
(This formula is applicable only when the limit is 0 to π/2).
Note that : 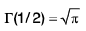
Walli’s formula
[An easy way to evaluate 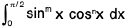 where m, n ∈ I+]
where m, n ∈ I+]
we have 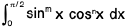
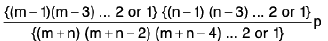
where p is π/2 if m and n are both even, otherwise p = 1. In last factor in each of the three products is either 1 or 2. In case of m or n is 1, we simply write 1 as the only factor to replace its product. If any of m or n is zero provided we put 1 as the only factor in its product and we regard 0 as even.
Problem on Greatest Integral Function
Example 96: Evaluate :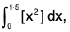 w here [.] denotes the greatest integer function .
w here [.] denotes the greatest integer function .
Analytical Method :
Value of x2 at x = 0 is 02 = 0 and at x = 1 -5 is (1 -5)2 = 2-25
∴ integers between 0 to 2-25 are 1 , 2
then x2 = 1 and x2 = 2 x = 1 and x = √2
=
=
= (2 - √2)
Graphical Method :
= = Area of shaded region
=
= (2 - √2)
Example 97: Prove that : 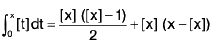 where [.] denotes the greatest integer function.
where [.] denotes the greatest integer function.
Analytical Method :
Let x = n + f ∀ n ∈ I and 0 ≤ f < 1
∴ [x] = n ----(1)
=
= 1 + 2 + 3 + ... + (n - 1) + nf
=
=
[from (1)}
Graphical Method :
Let x = n + f ∀ n ∈ I and 0 ≤ f < 1
∴ [x] = n ----(1)
= Area of shaded region
= 0 + 1 + 2 + ... + (n - 1) + (x - n) n
=
=
Example 98: Evaluate : 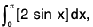 where [.] denotes the greatest integer function.
where [.] denotes the greatest integer function.
Analytical Method :
∵ 0 ≤ x < π
0 ≤ 2 sin x ≤ 2
Now when 2 sin x = 1⇒ sin x = 1/2
x = π/6, π/6
and If 0 ≤ 2 sinx < 1 , 0 < x < π/6 and
∴ [2 sin x] = 0 and If 1 ≤ 2 sin x < 2
∴
Now
=
Graphical Method:
= Area of shaded region
=
= 2π/3
|
98 videos|28 docs|30 tests
|
FAQs on Basic Integration- II - Mathematics for Competitive Exams
| 1. What is the geometrical interpretation of the definite integral? |  |
| 2. What are the properties of the definite integral? |  |
| 3. How can the definite integral be computed using the limit of a sum? |  |
| 4. How can integration be used to sum series? |  |
| 5. What is the gamma function? |  |


















































 =
= 



 -----(1)
-----(1) -----(2)
-----(2) then cos x =
then cos x = 









 ------(1)
------(1) or
or  ------(2)
------(2)































 = Area of shaded region
= Area of shaded region
 = Area of shaded region
= Area of shaded region 






































 ...(1)
...(1)
 ...(2)
...(2)







 ...(1)
...(1)
 ...(2)
...(2)





 ----(1)
----(1)
 ---(2)
---(2)









 ----(1)
----(1)
 ----(2)
----(2)








 ----(1)
----(1)





























 (here x is constant)
(here x is constant) ∴
∴ 



 (∴ Function is even)
(∴ Function is even)







 (∴ Function is even)
(∴ Function is even)


 ----(1)
----(1)
 ----(2)
----(2)







 then cos x dx =
then cos x dx = 










 (substitute t = 1- t)
(substitute t = 1- t)






 ( ∴ I cos x I is periodic with period π )
( ∴ I cos x I is periodic with period π )






 ( ∴I sin x I is periodic with period π )
( ∴I sin x I is periodic with period π )



 (∴ I sin x I is periodic with period π)
(∴ I sin x I is periodic with period π)  ( ∴ 0 ≤ V ≤ n )
( ∴ 0 ≤ V ≤ n )
























 where I‘(a) is the derivative of l(a)
where I‘(a) is the derivative of l(a) 













 is an odd function.
is an odd function. is not necessarily an odd function for a ≠ 0. It will be an odd function if
is not necessarily an odd function for a ≠ 0. It will be an odd function if 









 then
then 





 ---(1)≈
---(1)≈













 ...(1)
...(1)















 ⇒
⇒ 
 ∴
∴ 









































 = = Area of shaded region
= = Area of shaded region



 [from (1)}
[from (1)} = Area of shaded region
= Area of shaded region 






 = Area of shaded region
= Area of shaded region





















