Centroid & Center of Mass of the Composite Bodies | Engineering Mechanics - Civil Engineering (CE) PDF Download
What is the center of gravity?
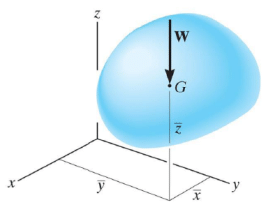
The center of gravity G is a point that locates the resultant weight of a system of particles.
What is the composite body?
A composite body consists of a series of connected simpler-shaped bodies, which may be rectangular, triangular, semicircular, etc.
What is centroid?

The line of action of the resultant force passes through the geometric center or centroid of the volume under the distributed–loading diagram.


Find the centroid of a rectangular area by integration



Find the centroid of a quarter circle by double integration in rectangular coordinates



Procedure for locating the center of gravity of a body or the centroid of a composite geometrical object
- Using a sketch, divide the body or object into a finite number of composite parts that have simpler shapes.
- If a composite part has a hole, or a geometric region having no material, then consider the composite part without the hole and consider the hole as an additional composite part having negative.
- Establish the coordinate axes on the sketch and determine the coordinates
 of the center of gravity or centroid of each part.
of the center of gravity or centroid of each part. - Determine
 by applying the center of gravity equations
by applying the center of gravity equations - If an object is symmetrical about an axis, the centroid of the object lies on this axis.
First Moments of Areas and Lines
|
|
 |
|
 |
|
Center of Mass – locates the point in a system where the resultant mass can be concentrated so that the moment of the concentrated mass with respect to any axis equals the moment of the distributed mass with respect to the same axis.

Center of gravity
The center of gravity (G) is a point that locates the resultant weight of a system of particles.
Particles with weights W1, W2, …, Wn can be replaced by a resultant force of weight W located at the center of gravity G.

To find the location of the center of gravity G(x,y,z):


(We can obtain z by imagining the coordinate system, with the particles fixed in it, as being rotated 90 degrees about the x (or the y) axis).
Knowing W=mg, if we assume that the acceleration due to gravity (g) for every particle is constant (g will be cancelled out)

A rigid body is composed of an infinite number of particles, hence it is necessary to use integration instead of summation.

But dm=ρdV, with ρ being the density and dv the volume of each particle. Therefore, the centre of mass has the coordinates of

Centroid:
The centroid (C) is a point that defines the geometric center of an object. If the material composing a body is uniform or homogeneous, the density of the material is constant (ρ = constant). Hence, the resulting formulas that define the centroid of a body depend only on the geometry of the body {Volume (V), Area (A), or Length (L)}.



Centroid (volume):

Centroid (area):

Centroid (line):

The centroids of some shapes may be partially or completely specified by using conditions of symmetry. In cases where the shape has an axis of symmetry, the centroid of the shape will lie along that axis.


|
24 videos|59 docs|53 tests
|
FAQs on Centroid & Center of Mass of the Composite Bodies - Engineering Mechanics - Civil Engineering (CE)
| 1. What is the difference between centroid and center of mass? |  |
| 2. How is the centroid of a composite body calculated? |  |
| 3. What is the significance of the centroid in civil engineering? |  |
| 4. Can the centroid of a composite body lie outside its boundaries? |  |
| 5. How is the center of mass of a composite body different from the centroid? |  |























