Basics of Straight Lines | Mathematics (Maths) Class 11 - Commerce PDF Download
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Introduction
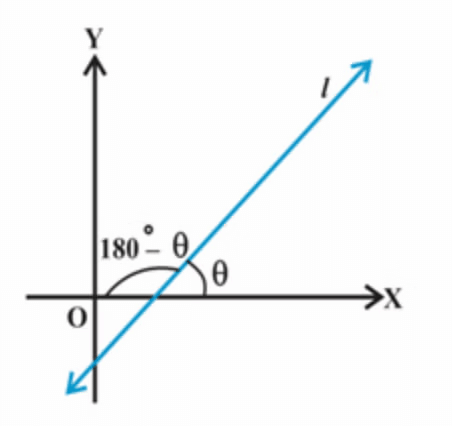
A line is considered as a geometrical shape with no breadth. It extends in both directions with no endpoints. It is a set of points and only has length. Lines can be parallel, perpendicular, intersecting or concurrent. A line in a coordinate plane forms two angles with the x-axis, which are supplementary. The angle (say) θ made by the line l with the positive direction of the x-axis and measured anti-clockwise is called the inclination of the line. Thus 0° ≤ θ ≤ 180°.
Slope of a Line
- The basics of straight lines start with a slope. A slope is an inclined position. It forms a certain angle with the base.
- How can we find a slope of a line? In the coordinate geometry, if any line l makes an angle θ with the positive direction of x-axis, it is called the Inclination of the line.
- The angle is measured in an anti-clockwise way. A slope of a line is the tangent of the inclination, θ i.e., tan θ. It is denoted as m.
Thus, the slope of a line:
m = tan θ, θ ≠ 90°.
➤ Slope of a Line When Coordinates of Any Points on the Lines Are Given
- Imagine a line l with a slope θ. Two points A (x1, y1) and B (x2, y2) lies on it. The angle of inclination can be acute or obtuse.
(i) Case 1: θ is acute

Here, ∠CAB = θ. The slope of the line, m = tan θ.
In ΔCAB, tan θ = CB/CA = (y2 − y1)/(x2 − x1).
Thus, m = tan θ = (y2 − y1)/(x2 − x1).
(ii) Case 2: θ is obtuse
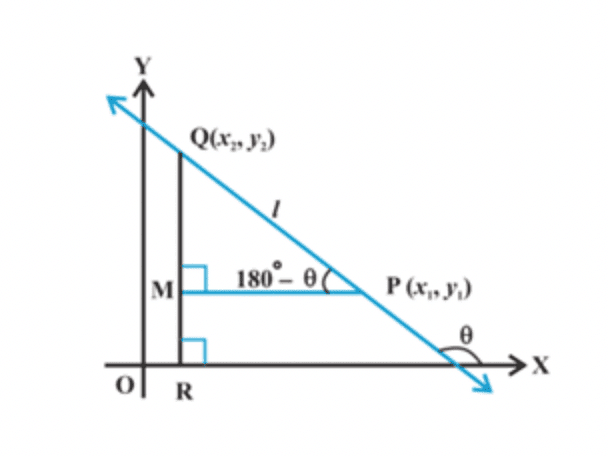
Here, ∠CAB =180° − θ.Slope of the line, m = tan θ = tan (180°− ∠CAB) = − tan ∠CAB
m = − CB/CA = − (y2 − y1)/(x1 − x2).
Thus, m = tan θ = (y2 − y1)/(x2 − x1).
➤ Conditions for Parallelism of Lines in Terms of Slopes
Two lines are parallel if the distance between them at any point remains the same. It can also be inferred that the slopes of the two lines must be the same. Let two lines l1 and l2 have respective slopes m1 and m2 and angle of inclinations α and β. The lines will be parallel if α = β i.e., m1 = m2 and tanα = tanβ
➤ Conditions for Perpendicularity of Lines in Terms of Slopes
Two lines are perpendicular if they intersect each other at an angle of 90°. Let two lines l1 and l2 have respective slopes m1 and m2 and angle of inclinations α and β. Here, α = β + 90°.
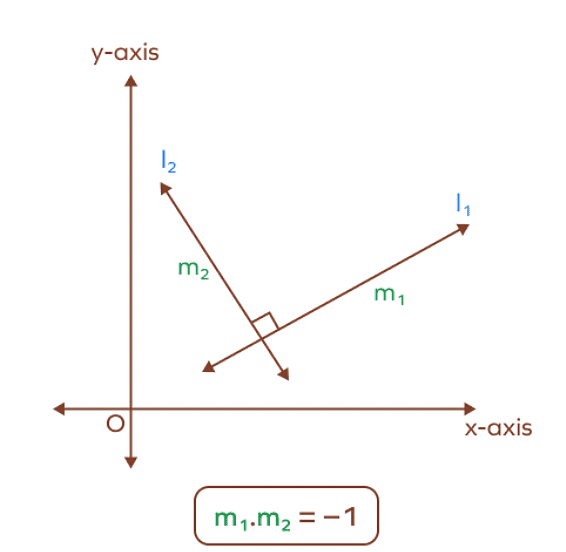
tan α= tan (β + 90°) = − cot β = − 1/tan β
or, m2 = −1 /m1 or m1m2 = −1
The lines will be perpendicular if and only if m2 = −1/m1 or m1m2 = −1.
➤ Angle Between Two Lines
Above we get to know about parallel and perpendicular lines. How can we find out the angle between two intersecting lines (other than 90°)? Let two lines l1 and l2 have respective slopes m1 and m2 and angle of inclinations α1 & α2. Or, m1= tan α1 & m2 = tan α2

From the property of angle:
θ = α1 − α2
⇒ tan θ = tan (α1 − α2) = (tanα1 − tanα2)/ (1+ tanα1 tanα2) = (m1−m2)/ (1+m1m2)
and Φ = 180° − θ,
⇒ tan Φ = tan (180° − θ) = − tan θ = − (m1−m2) / (1+m1m2)
1 + m1m2 ≠ 0
➤ Collinearity of Three Points
Three points are collinear if they all lie on the same line. Three points A(x1,y1), B(x2,y2) and C(x3,y3) are collinear iff slope of AB = slope of BC i.e., (y2 − y1)/(x2 − x1) = (y3 − y2)/(x3 − x2).

Solved Examples
Problem 1. What is the slope of the horizontal line and vertical line
Solution: The slope of horizontal line is zero (m = 0, θ = 0°). The slope of a vertical line is undefined (θ= 90°).
Problem 2. Find the slope of the line passing through the points (4, 3) and (1, 5).
Solution: Slope of the line, m = (y2 − y1)/(x2 − x1) = (5 − 3) / (1 − 4) = −2/3.
Problem 3. Find the value of x, if the points (1, −1), (x, 1) and (6, 7) are collinear.
Solution: Three points are collinear if (y2 − y1)/(x2 − x1) = (y3 − y2)/(x3 − x2) . Putting the values, we have, (1 − (−1))/(x − 1) = (7 − 1)/(6 − x) or, 2(6 − x) = 6(x − 1). Or, x = 9/4.
|
75 videos|238 docs|91 tests
|
FAQs on Basics of Straight Lines - Mathematics (Maths) Class 11 - Commerce
| 1. What are the basics of straight lines in Airforce X Y/Indian Navy SSR? |  |
| 2. How are straight lines related to the Airforce X Y/Indian Navy SSR exam? |  |
| 3. What are some examples of questions related to straight lines in the Airforce X Y/Indian Navy SSR exam? |  |
| 4. How can I prepare effectively for the straight lines topic in the Airforce X Y/Indian Navy SSR exam? |  |
| 5. Are there any specific tips or tricks for solving straight line problems in the Airforce X Y/Indian Navy SSR exam? |  |

|
Explore Courses for Commerce exam
|

|
























