Bayes' Theorem | Additional Topics for IIT JAM Mathematics PDF Download
13.5 Bayes' Theorem
Consider that there are two bags I and II. Bag I contains 2 white and 3 red balls and Bag II contains 4 white and 5 red balls. One ball is drawn at random from one of the bags. We can find the probability of selecting any of the bags  or probability of drawing a ball of a particular colour (say white) from a particular bag (say Bag I). In other words, we can find the probability that the ball drawn is of a particular colour, if we are given the bag from which the ball is drawn. But, can we find the probability that the ball drawn is from a particular bag (say Bag II), if the colour of the ball drawn is given? Here, we have to find the reverse probability of Bag II to be selected when an event occurred after it is known. Famous mathematician, John Bayes' solved the problem of finding reverse probability by using conditional probability. The formula developed by him is known as ‘Bayes theorem’ which was published posthumously in 1763.
or probability of drawing a ball of a particular colour (say white) from a particular bag (say Bag I). In other words, we can find the probability that the ball drawn is of a particular colour, if we are given the bag from which the ball is drawn. But, can we find the probability that the ball drawn is from a particular bag (say Bag II), if the colour of the ball drawn is given? Here, we have to find the reverse probability of Bag II to be selected when an event occurred after it is known. Famous mathematician, John Bayes' solved the problem of finding reverse probability by using conditional probability. The formula developed by him is known as ‘Bayes theorem’ which was published posthumously in 1763.
Before stating and proving the Bayes' theorem, let us first take up a definition and some preliminary results.
13.5.1 Partition of a sample space
A set of events E1, E2, ..., En is said to represent a partition of the sample space S if
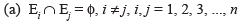
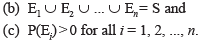
In other words, the events E1, E2, ..., En represent a partition of the sample space S if they are pairwise disjoint, exhaustive and have nonzero probabilities.
As an example, we see that any nonempty event E and its complement E′ form a partition of the sample space S since they satisfy E ∩ E′ = φ and E ∪ E′ = S.
From the Venn diagram in Fig 13.3, one can easily observe that if E and F are any two events associated with a sample space S, then the set {E ∩ F′, E ∩ F, E′ ∩ F, E′ ∩ F′} is a partition of the sample space S. It may be mentioned that the partition of a sample space is not unique. There can be several partitions of the same sample space.
We shall now prove a theorem known as Theorem of total probability.
13.5.2 Theorem of total probability
Let {E1, E2,...,En} be a partition of the sample space S, and suppose that each of the events E1, E2,..., En has nonzero probability of occurrence. Let A be any event associated with S, then
P(A) = P(E1) P(A|E1) + P(E2) P(A|E2) + ... + P(En) P(A|En)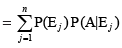
Proof Given that E1, E2,..., En is a partition of the sample space S (Fig 13.4). Therefore,
S = E1 ∪ E2 ∪ ... ∪ En ... (1)
and Ei ∩ Ej = φ, i ≠ j, i, j = 1, 2, ..., n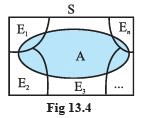
Now, we know that for any event A,
A = A ∩ S
= A ∩ (E1 ∪ E2 ∪ ... ∪ En)
= (A ∩ E1) ∪ (A ∩ E2) ∪ ...∪ (A ∩ En)
Also A ∩ Ei and A ∩ Ej are respectively the subsets of Ei and Ej. We know that Ei and Ej are disjoint, for i ≠ j , therefore, A ∩ Ei and A ∩ Ej are also disjoint for all i ≠ j, i, j = 1, 2, ..., n.
Thus, P(A) = P [(A ∩ E1) ∪ (A ∩ E2)∪ .....∪ (A ∩ En)]
= P (A ∩ E1) + P (A ∩ E2) + ... + P (A ∩ En)
Now, by multiplication rule of probability, we have P(A ∩ Ei) = P(Ei) P(A|Ei) as P(Ei) ≠ 0∀i = 1,2,..., n
Therefore, P (A) = P (E1) P (A|E1) + P (E2) P (A|E2) + ... + P (En)P(A|En)
or 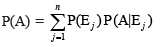
Example 15. A person has undertaken a construction job. The probabilities are 0.65 that there will be strike, 0.80 that the construction job will be completed on time if there is no strike, and 0.32 that the construction job will be completed on time if there is a strike. Determine the probability that the construction job will be completed on time.
Solution. Let A be the event that the construction job will be completed on time, and B be the event that there will be a strike. We have to find P(A).
We have
P(B) = 0.65, P(no strike) = P(B′) = 1 − P(B) = 1 − 0.65 = 0.35
P(A|B) = 0.32, P(A|B′) = 0.80
Since events B and B′ form a partition of the sample space S, therefore, by theorem on total probability, we have P(A) = P(B) P(A|B) + P(B′) P(A|B′)
= 0.65 × 0.32 + 0.35 × 0.8
= 0.208 + 0.28 = 0.488
Thus, the probability that the construction job will be completed in time is 0.488.
We shall now state and prove the Bayes' theorem.
Bayes’ Theorem If E1, E2 ,..., En are n non empty events which constitute a partition of sample space S, i.e. E1, E2 ,..., En are pairwise disjoint and E1∪ E2∪ ... ∪ En = S and A is any event of nonzero probability, then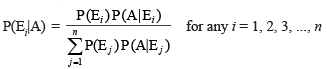
Proof By formula of conditional probability, we know that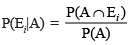
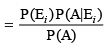 (by multiplication rule of probability)
(by multiplication rule of probability)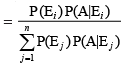 (by the result of theorem of total probability)
(by the result of theorem of total probability)
Remark. The following terminology is generally used when Bayes' theorem is applied.
The events E1, E2, ..., En are called hypotheses.
The probability P(Ei) is called the priori probability of the hypothesis Ei The conditional probability P(Ei |A) is called a posteriori probability of the hypothesis Ei.
Bayes' theorem is also called the formula for the probability of "causes". Since the Ei's are a partition of the sample space S, one and only one of the events Ei occurs (i.e. one of the events Ei must occur and only one can occur). Hence, the above formula gives us the probability of a particular Ei (i.e. a "Cause"), given that the event A has occurred.
The Bayes' theorem has its applications in variety of situations, few of which are illustrated in following examples.
Example 16. Bag I contains 3 red and 4 black balls while another Bag II contains 5 red and 6 black balls. One ball is drawn at random from one of the bags and it is found to be red. Find the probability that it was drawn from Bag II.
Solution. Let E1 be the event of choosing the bag I, E2 the event of choosing the bag II and A be the event of drawing a red ball.
Then P(E1) = P(E2) = 1/2
Also P(A|E1) = P(drawing a red ball from Bag I) = 3/7
and P(A|E2) = P(drawing a red ball from Bag II) = 5/11
Now, the probability of drawing a ball from Bag II, being given that it is red, is P(E2|A) By using Bayes' theorem, we have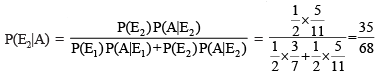
Example 17. Given three identical boxes I, II and III, each containing two coins. In box I, both coins are gold coins, in box II, both are silver coins and in the box III, there is one gold and one silver coin. A person chooses a box at random and takes out a coin. If the coin is of gold, what is the probability that the other coin in the box is also of gold?
Solution. Let E1, E2 and E3 be the events that boxes I, II and III are chosen, respectively.
Then P(E1) = P(E2) = P(E3) = 1/3
Also, let A be the event that ‘the coin drawn is of gold’
Then P(A|E1) = P(a gold coin from bag I) = 2/2 = 1
P(A|E2) = P(a gold coin from bag II) = 0
P(A|E3) = P(a gold coin from bag III) = 1/2
Now, the probability that the other coin in the box is of gold
= the probability that gold coin is drawn from the box I.
= P(E1|A)
By Bayes' theorem, we know that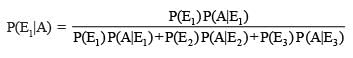
Example 18. Suppose that the reliability of a HIV test is specified as follows:
Of people having HIV, 90% of the test detect the disease but 10% go undetected. Of people free of HIV, 99% of the test are judged HIV–ive but 1% are diagnosed as showing HIV+ive. From a large population of which only 0.1% have HIV, one person is selected at random, given the HIV test, and the pathologist reports him/her as HIV+ive. What is the probability that the person actually has HIV?
Solution. Let E denote the event that the person selected is actually having HIV and A the event that the person's HIV test is diagnosed as +ive. We need to find P(E|A).
Also E′ denotes the event that the person selected is actually not having HIV.
Clearly, {E, E′} is a partition of the sample space of all people in the population.
We are given that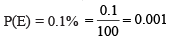
P(E′) = 1 – P(E) = 0.999
P(A|E) = P(Person tested as HIV+ive given that he/she is actually having HIV)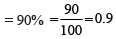
and P(A|E′) = P(Person tested as HIV +ive given that he/she is actually not having HIV)
= 1% = 1/100 = 0.01
Now, by Bayes' theorem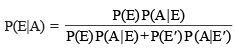

Thus, the probability that a person selected at random is actually having HIV given that he/she is tested HIV+ive is 0.083.
Example 19. In a factory which manufactures bolts, machines A, B and C manufacture respectively 25%, 35% and 40% of the bolts. Of their outputs, 5, 4 and 2 percent are respectively defective bolts. A bolt is drawn at random from the product and is found to be defective. What is the probability that it is manufactured by the machine B?
Solution. Let events B1, B2, B3 be the following :
B1 : the bolt is manufactured by machine A
B2 : the bolt is manufactured by machine B
B3 : the bolt is manufactured by machine C
Clearly, B1, B2, B3 are mutually exclusive and exhaustive events and hence, they represent a partition of the sample space.
Let the event E be ‘the bolt is defective’.
The event E occurs with B1 or with B2 or with B3. Given that,
P(B1) = 25% = 0.25, P (B2) = 0.35 and P(B3) = 0.40
Again P(E|B1) = Probability that the bolt drawn is defective given that it is manufactured by machine A = 5% = 0.05
Similarly, P(E|B2) = 0.04, P(E|B3) = 0.02.
Hence, by Bayes' Theorem, we have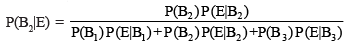
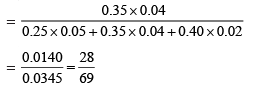
Example 20. A doctor is to visit a patient. From the past experience, it is known that the probabilities that he will come by train, bus, scooter or by other means of transport are respectively 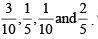 The probabilities that he will be late are
The probabilities that he will be late are 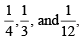 if he comes by train, bus and scooter respectively, but if he comes by other means of transport, then he will not be late. When he arrives, he is late. What is the probability that he comes by train?
if he comes by train, bus and scooter respectively, but if he comes by other means of transport, then he will not be late. When he arrives, he is late. What is the probability that he comes by train?
Solution. Let E be the event that the doctor visits the patient late and let T1, T2, T3, T4 be the events that the doctor comes by train, bus, scooter, and other means of transport respectively.
Then 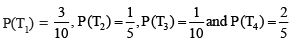 (given)
(given)
P(E|T1) = Probability that the doctor arriving late comes by train = 1/4
Similarly, P(E|T2) = 1/3, P(E|T3) = 1/12 and P(E|T4) = 0, since he is not late if he comes by other means of transport.
Therefore, by Bayes' Theorem, we have
P(T1|E) = Probability that the doctor arriving late comes by train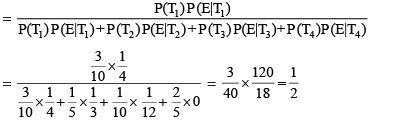
Hence, the required probability is 1/2
Example 21. A man is known to speak truth 3 out of 4 times. He throws a die and reports that it is a six. Find the probability that it is actually a six.
Solution. Let E be the event that the man reports that six occurs in the throwing of the die and let S1 be the event that six occurs and S2 be the event that six does not occur.
Then P(S1) = Probability that six occurs = 1/6
P(S2) = Probability that six does not occur = 5/6
P(E|S1) = Probability that the man reports that six occurs when six has actually occurred on the die = Probability that the man speaks the truth = 3/4
P(E|S2) = Probability that the man reports that six occurs when six has not actually occurred on the die
= Probability that the man does not speak the truth 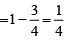
Thus, by Bayes' theorem, we get
P(S1|E) = Probability that the report of the man that six has occurred is actually a six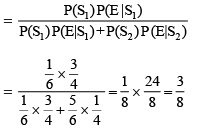
Hence, the required probability is 3/8.
|
2 videos|44 docs|4 tests
|
FAQs on Bayes' Theorem - Additional Topics for IIT JAM Mathematics
| 1. What is Bayes' Theorem and how is it used in mathematics? |  |
| 2. How is Bayes' Theorem applied in real-life scenarios? |  |
| 3. What are the main components of Bayes' Theorem? |  |
| 4. Can Bayes' Theorem be used with multiple events or conditions? |  |
| 5. Are there any limitations or assumptions associated with Bayes' Theorem? |  |

















